Coordonnées matérielles
Variété matérielle
Notre approche des grandes transformations est basée sur l'utilisation parallèle des deux configurations lagrangienne (bleue, configuration de référence Co) et eulérienne (rouge, configuration actuelle C(t) ). Les coordonnées lagrangiennes X I (non, ce n'est pas une erreur, l'indice I est bien maintenant en haut, nous y viendrons bientôt) définissent sur Co un système de coordonnées cartésiennes orthonormées et nous noterons EI les vecteurs de base correspondants
X = X I EI EI . EJ = δIJ
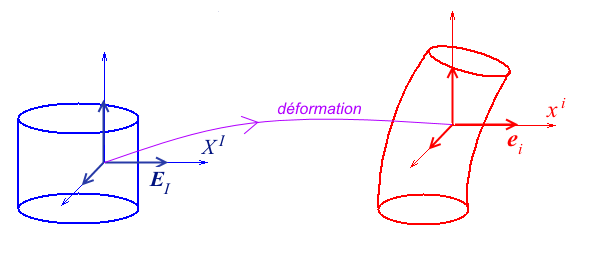
Toutefois, s'il est souvent pratique de choisir cette configuration de référence Co comme étant la configuration initiale C(0), ceci n'est qu'une commodité. Les coordonnées lagrangiennes servent avant tout à identifier des particules. Leur immersion dans l'espace physique est commode mais peut aussi masquer leur signification réelle. A ce titre il importe de considérer notre milieu continu comme une variété abstraite souvent notée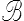 
(comme body) et les X I comme un paramétrage de cette variété (une « carte » dans le langage de la géométrie différentielle). Une configuration est alors une application suffisamment régulière (continue, différentiable,...) de cette variété matérielle dans l'espace euclidien 
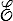(on parle souvent de « placement »).
Cette nuance d'interprétation et de terminologie (variété matérielle plutôt que configuration de référence) recouvre en fait un changement complet de perspective et conduit à une formulation alternative de la MMC en grandes transformations. Ce n'est pas celle que j'ai choisie, et j'évoquerai plus loin les raisons − notamment pédagogiques − de ce choix. Elle n'en est pas moins respectable et il est important d'en connaître les grandes lignes. C'est l'objectif de cette page.
Un milieu continu, un bloc de matière, est donc essentiellement une variété différentiable 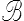, paramétrée par diverses cartes − notamment les placements qu'elle occupe au cours du temps. C'est incontestablement le bon cadre mathématique. On a donc besoin du langage et des outils de la géométrie différentielle. Je les évoquerai à petites doses et au fil de l'eau, mais une approche sérieuse nécessiterait un long « rappel » de géométrie différentielle avant de pouvoir vraiment aborder la mécanique. C'est un point de vue tout à fait estimable mais qui, à mon avis, nous éloignerait trop ici de la physique. Le champ des vitesses par exemple est alors (je crois) un élément du fibré tangent à !!!
C'est l'une des raisons − pédagogique − qui me conduit à privilégier l'approche Lagrange-Euler développée jusqu'à présent.
Le lecteur est ici en droit de se sentir soulagé et de quitter cette page pour passer à la suivante. C'est possible, mais je vous incite toutefois à faire l'effort d'insister un peu. Au-delà de la technique un peu lourde, et sur laquelle vous pourrez revenir plus tard, les idées et représentations que nous allons développer sont utiles et importantes.
Bases matérielles et tenseurs métriques
La variété matérielle , paramétrée par les coordonnées matérielles X I est à chaque instant t (et aussi en particulier pour t = 0 si l'on souhaite faire jouer un rôle particulier à la configuration initiale C(0) ) immergée dans l'espace euclidien par le placement
x = x i ei ei . ej = δij x i = x i (X J,t)
(repère cartésien orthonormé).
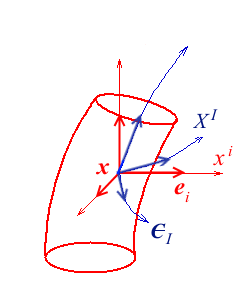Les coordonnées matérielles X J définissent sur la configuration C = C(t) un système de coordonnées curvilignes. Un vecteur matériel dx est alors
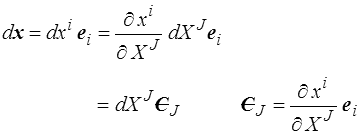
Les 3 vecteurs (1 ,2 ,3 ), tangents aux lignes coordonnées, constituent la base matérielle. Elle n'est pas orthonormée et cela complique fortement les choses. En particulier la convention de sommation (<) s'applique maintenant sur des couples d'indices placés l'un en position haute (contravariante) et l'autre en position basse (covariante). Attention toutefois, la dérivation par rapport à un indice contravariant est covariante. On note parfois
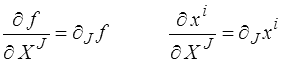
Les vecteurs et tenseurs de l'espace physique peuvent bien entendu être définis par leurs composantes dans cette base matérielle.
La base matérielle duale (contravariante) est ensuite définie par
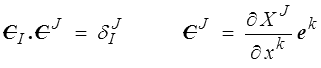
On remarquera que pour être cohérent avec nos nouvelles conventions de notation, nous avons noté ici les vecteurs de base avec un indice supérieur − même pour la base spatiale que nous garderons orthonormée
V = Vi e i = V i ei ( ei = e i Vi = V i )
C'est justement pour éviter cette distinction covariant-contravariant que nous avons à maintes reprises insisté sur l'utilisation de repères orthonormés. En coordonnées matérielles X J, ce n'est malheureusement plus possible. Cette base contravariante peut apparaître naturellement par exemple pour le gradient d'une fonction scalaire
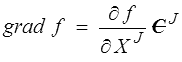
De même tout vecteur V pourra être défini à partir de ses composantes matérielles covariantes VI ou contravariantes V I
V = VI I = V I I
En coordonnées matérielles on pourra donc utiliser les bases covariantes et/ou contravariantes. Pour passer de l'une à l'autre on utilise le « tenseur métrique », c'est-à-dire tout simplement dans notre espace euclidien l'identité
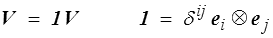
application linéaire identité représentée dans le repère cartésien orthonormé ei par la matrice unité. Cette terminologie « métrique » provient du fait que ce tenseur définit en réalité le produit scalaire et la distance. On écrira en général
I .J = GIJ I. J = G IJ
où les deux matrices de composantes GIJ et G IJ sont inverses l'une de l'autre. On vérifie alors directement que ces matrices permettent le passage covariant ↔ contravariant. Par exemple
I = G IJ J VI = V .I V I = V . I
et ainsi de suite.
Composantes matérielles
Pour relier ces bases matérielles à la base cartésienne de départ on écrit simplement
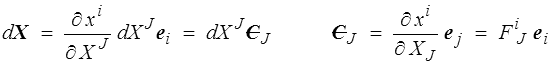
Les composantes de la matrice de passage de la base cartésienne orthonormée à la base matérielle covariante correspondent aux composantes cartésiennes du tenseur gradient F. Les composantes matérielles du tenseur symétrique s'obtiennent ensuite simplement
GIJ = I .J = δkl F kI F lJ = CIJ
et on retrouve les composantes cartésiennes du tenseur de Cauchy-Green droit (<) . Ainsi les composantes (cartésiennes orthonormées et dans Co ) du tenseur lagrangien de Cauchy-Green droit peuvent aussi être interprétées comme les composantes covariantes dans C du tenseur métrique
De la même manière le tenseur (eulérien) des contraintes de Kirchhoff est relié au second tenseur de Piola-Kirchhoff (<)
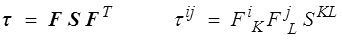
de sorte que l'on peut écrire
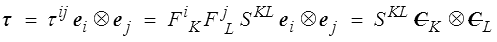
Les composantes (cartésiennes orthonormées) du tenseur PK2 (lagrangien) peuvent aussi être considérées comme les composantes matérielles contravariantes du tenseur (eulérien) de Kirchhoff
Les composantes (cartésiennes) des tenseurs lagrangiens peuvent ainsi s'interpréter également comme les composantes matérielles de tenseurs eulériens, on évite ainsi le retour à la configuration de référence Co. On peut aussi espérer, et c'est en fait justifié (comme nous le verrons plus loin), que l'utilisation de cette description matérielle, plus proche de la matière, conduise à des formulations plus intrinsèques.
En tout état de cause, l'essentiel de la Mécanique des Milieux Continus peut se construire en coordonnées matérielles et donc sans référence explicite à la configuration de référence Co. On retrouvera ce point de vue alternatif utilisé comme point de départ dans de nombreux ouvrages.
Dérivées convectives
Soit M un tenseur (du second ordre et symétrique pour fixer les idées, mais cela s'adapte à d'autres cas). Nous savons maintenant lui associer des composantes matérielles covariantes et contravariantes
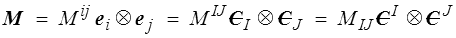
La dérivée temporelle de ce tenseur est simplement
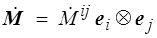
Toutefois son expression à partir des composantes matérielles est moins simple, car il faut prendre en compte, en plus de la dérivée des composantes, celle des vecteurs de base qui, eux aussi, changent au cours du temps. Parallèlement on peut aussi considérer les « dérivées » obtenues par dérivation de ces seules composantes et définir par exemple la dérivée convective covariante par
L'idée sous-jacente est que cette dérivée temporelle représente mieux que la dérivée ordinaire la variation du tenseur M telle qu'elle est ressentie par la matière, puisque rapportée à la base matérielle qui suit la matière dans son mouvement. Nous aurons l'occasion d'y revenir. Pour la calculer nous écrivons
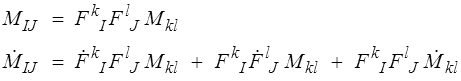
mais la dérivée temporelle de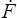 
kI (on remarquera que j'évite de parler de tenseur gradient, il s'agit dans ce contexte d'une matrice de passage) sera donnée par
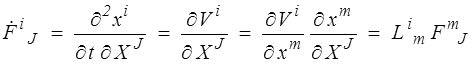
où les Lim sont les composantes (cartésiennes orthonormées, la position haute ou basse des indices n'est maintenue que pour la cohérence de l'écriture) du tenseur gradient des vitesses
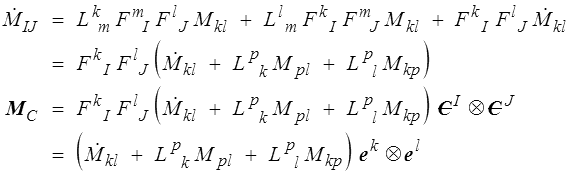
en remarquant que
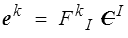
Les composantes cartésiennes orthonormées du tenseur MC sont donc
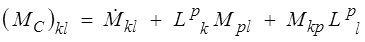
soit tensoriellement
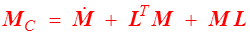
On définirait et calculerait de la même manière la dérivée convective contravariante
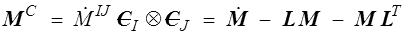
Nous avons évoqué plus haut (<) , les difficultés qui apparaissent pour la dérivation temporelle des tenseurs eulériens. Les dérivées convectives que nous venons d'introduire fournissent une solution.
A titre d'exemple on peut remarquer que le tenseur des taux de déformation est la dérivée convective du tenseur métrique
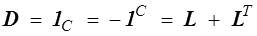
ou bien encore que la dérivée convective contravariante du tenseur de Cauchy-Green gauche est nulle
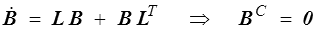
Equation constitutive
Pour décrire le comportement du matériau, la relation contraintes-déformations s'écrira naturellement en composantes matérielles. Nous écrirons donc une relation (fonctionnelle) entre les composantes matérielles du tenseur des contraintes de Kirchhoff et du tenseur métrique (nous n'avons pas défini de déformation, mais c'est le tenseur métrique qui porte l'information correspondante). Nous écrirons donc une relation matricielle entre les matrices des composantes matérielles de ces tenseurs
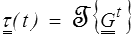
Si nous choisissons pour τ les composantes contravariantes et pour le tenseur métrique les composantes covariantes, alors τ IJ sera une fonctionnelle de l'histoire des composantes covariantes du tenseur métrique. Mais nous avons vu que ces composantes matérielles coïncidaient avec les composantes cartésiennes orthonormées des tenseurs lagrangiens S et C
τ IJ = S IJ GIJ = CIJ
En revenant à nos notations (tensorielles) usuelles ceci équivaut donc à écrire une loi de comportement
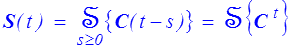
C'est un cas particulier de la loi de comportement générale écrite précédemment (<) . Toutefois nous montrerons que, en appliquant à cette forme générale le principe d'indifférence matérielle, on retombe exactement sur cette forme réduite lagrangienne qui s'avère être en fait la loi de comportement générale d'un milieu matériellement simple.
Cette formulation en coordonnées matérielles implique donc automatiquement le principe d'indifférence matérielle qui, dans ce cadre, n'a donc plus lieu d'être. C'est bien évidemment un avantage certain.