Calcul tensoriel
Notations tensorielles intrinsèques
Les notations indicielles (<) sont, pour manipuler vecteurs et tenseurs, utiles et précises. Elles sont toutefois parfois lourdes et nous leur préférerons souvent dans ce cours des notations tensorielles directes, traitant vecteurs et tenseurs comme des êtres géométriques autonomes, indépendamment de tout repère. Nous l'avons déjà parfois fait en écrivant par exemple (<)
T = σ n pour Ti = σij nj
mais nous le ferons beaucoup plus systématiquement désormais. Il importe donc de clarifier les conventions. Nous noterons donc sans symbole le produit simple
T = σ n Ti = σij nj
C = A B Cik = Aij Bjk
ce qui correspond, une fois choisie une base (toujours orthonormée, rappelons-le), au simple produit matriciel.
Nous noterons d'un point le produit scalaire de deux vecteurs et de deux points celui de deux tenseurs
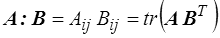
avec notamment les règles de transformation
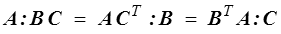
formules importantes dans les manipulations que nous aurons à faire.
Pour un tenseur du second ordre (<) quelconque
A∈ 
, nous noterons
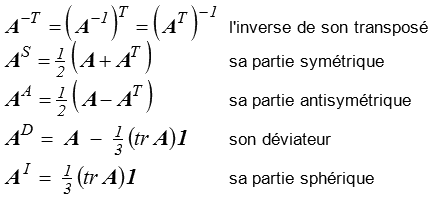
Ces notations trouvent par contre leurs limites dès que l'on dépasse les tenseurs d'ordre deux, il faudra alors revenir aux notations indicielles, avec toutefois une exception : les tenseurs d'ordre 4, applications linéaires de 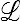dans 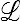, seront notés
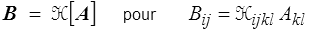
avec par exemple des relations comme
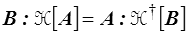
où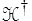 
est l'adjoint de 
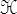. La loi de l'élasticité linéaire (<)
s'écrit par exemple ainsi
avec un tenseur d'élasticité auto-adjoint, ce qui correspond aux conditions de symétrie que doit vérifier le tenseur d'élasticité .
Invariants. Cayley-Hamilton
Les valeurs propres A1, A2, A3 d'un tenseur symétrique A sont les 3 racines de son équation caractéristique
P( λ ) = det (A − λ1) = 0
Les invariants fondamentaux (<) de A sont les coefficients du polynôme caractéristique
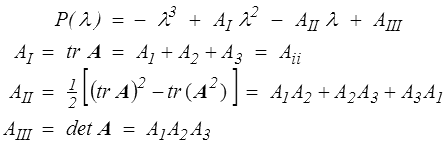
On parle d'invariant car leur expression à partir des composantes est invariante par changement de repère (orthonormé bien sûr), leur caractère fondamental apparaîtra bientôt.
On démontre (par exemple en se plaçant en repère principal),
Théorème de Cayley-Hamilton.
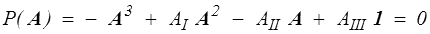
Un tenseur symétrique est solution de son équation caractéristique.
C'est un résultat essentiel avec de nombreuses applications. En en prenant la trace par exemple, on en déduit une expression du déterminant
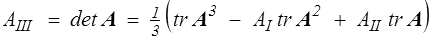
On pourrait d'ailleurs utiliser comme ensemble d'invariants tr A, tr A2 et tr A3. En effet
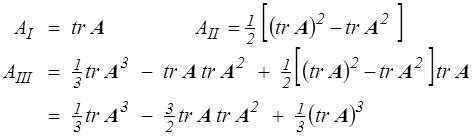
Si A est inversible (AIII ≠ 0 ) on obtient aussi, en multipliant par A − 1, une expression de l'inverse
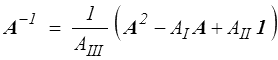
Fonctions tensorielles
Une fonction tensorielle (scalaire) est une application de 
dans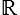 
qui à tout tenseur symétrique associe un nombre. Elle pourra être définie de manière intrinsèque ou par son expression en fonction des composantes Xij du tenseur dans un repère donné.
f ( X ) = f ( X )
en notant X la matrice Xij. La fonction f dépendra bien évidemment du repère choisi et, en notant Q la matrice de changement de base (<), on obtient directement son expression dans un autre repère
f ( X ) = f ( X ) = f ' ( X ' ) X ' = Q X QT
Une condition nécessaire et suffisante pour que cette fonction matricielle soit la même dans chaque repère est qu'elle vérifie
f ( X ) = f ( Q X QT ) pour toute matrice Q orthogonale
Une fonction vérifiant cette propriété est dite isotrope. Attention toutefois à ne pas confondre cette notion avec l'isotropie ou l'anisotropie éventuelle d'un matériau. Pour éviter cette confusion je parlerai dans ce cas d'une fonction m-isotrope (isotropie au sens mathématique du terme). Bien évidemment ces fonctions joueront un rôle important dans la description des matériaux isotropes ou anisotropes, mais ce sont des notions différentes qu'il importe de ne pas confondre.
Par extension nous dirons aussi que la fonction tensorielle f ( X ) est m-isotrope si elle vérifie la condition
f ( Q X QT ) = f ( X ) ∀ Q ∈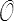 
où 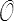est le groupe orthogonal (groupe de toutes les rotations).
Les invariants, ou plus généralement toute fonction des invariants, sont des fonctions m-isotropes, mais si par exemple a est un vecteur unitaire la fonction définie par
f ( X ) = a . X a
n'est pas m-isotrope : c'est la fonction qui à X associe sa composante X11 dans un repère où e1 = a.
On définira de même des fonctions tensorielles applications de 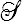dans 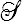, et on dira qu'elles sont m-isotropes si
F ( Q X QT ) = Q F ( X ) QT ∀ Q ∈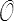
Ce sera le cas par exemple des fonctions usuelles classiques comme l'exponentielle, le logarithme, la racine carrée ou plus généralement une puissance entière ou non entière. Rappelons que ces fonctions sont des tenseurs ayant les mêmes directions principales que X et dont les valeurs propres sont les fonctions correspondantes des valeurs propres de X.
Nous nous sommes ici limités aux tenseurs symétriques, mais l'ensemble s'étend directement aux vecteurs, tenseurs non symétriques, etc... Par exemple une fonction de E×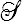 dans 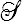sera m-isotrope si
F ( Q v, Q X QT ) = Q F ( v, X ) QT
et ainsi de suite. Attention toutefois, sitôt qu'interviendront des vecteurs ou des tenseurs d'ordre impair il faudra distinguer
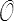groupe orthogonal = { Q ; Q QT = 1 }
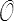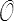+ ⊂ groupe des rotations = { Q ; Q QT = 1, det Q = +1 }
Dérivation
Si f ( X ) est une fonction tensorielle sa dérivée est définie par la dérivée des composantes
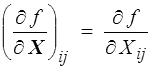
On vérifie sans peine que c'est un tenseur.
Par exemple pour l'application
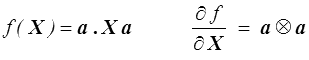
car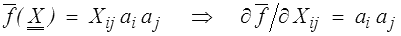 
, introduisant le produit tensoriel (<) du vecteur a par lui même.
Pour calculer cette dérivée, il sera souvent plus commode de passer par l'intermédiaire de la différentielle
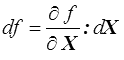
Par exemple pour calculer la dérivée de la fonction tr X3
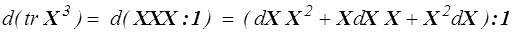
mais en utilisant les règles vues plus haut (<)
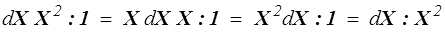
il vient finalement
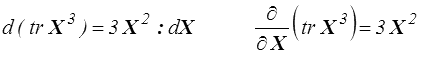
et plus généralement pour tout m entier positif
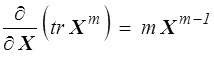
Cet exemple montre bien que, sans être très difficiles, ces calculs demandent quelques précautions. En particulier il serait tentant de généraliser cette sympathique relation à tout exposant m (négatif, rationnel, réel). Malheureusement notre calcul ne fonctionne que dans le cas d'un entier positif.
Nous aurons plus loin besoin de la dérivée des invariants fondamentaux XI , XII et XIII
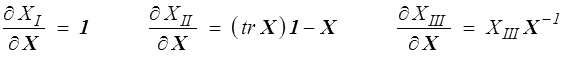
Pour les deux premiers c'est facile ; par exemple
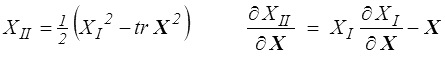
Pour le troisième c'est un peu plus laborieux. On peut par exemple partir de l'expression obtenue plus haut pour XIII en fonction de tr X , tr X2 et tr X3 et utiliser le résultat obtenu pour la trace d'une puissance pour retomber sur la valeur de X −1 tirée de l'identité de Cayley-Hamilton. Je laisse le détail du calcul au lecteur consciencieux. On tire en particulier de cette troisième relation une formule utile:
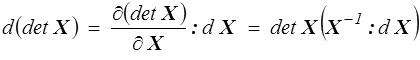
Si l'on part d'une fonction à valeur tensorielle on peut toujours définir une dérivée, mais ce sera alors un tenseur d'ordre 4, et tout devient beaucoup plus compliqué.
Approfondissons un peu
Pour calculer cette dernière dérivée, nous aurions aussi pu partir de l'expression du déterminant XIII à partir des valeurs propres de X
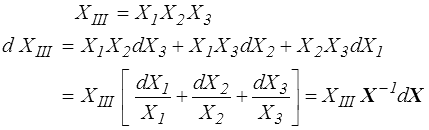
en remarquant naïvement que, en repère principal,
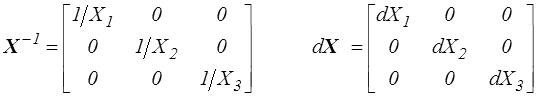
Mais c'est justement un peu trop naïf car si on peut toujours se placer dans le repère principal de X, sa différentielle dX n'a par contre aucune raison d'être diagonale, de sorte que l'on peut seulement écrire
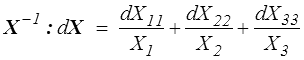
et on ne peut pas conclure.
C'est bien dommage, mais tout n'est pas perdu ! Attention toutefois accrochez vos ceintures et vous pouvez sans dommage majeur passer directement à la conclusion de ce paragraphe. En supposant les 3 valeurs propres distinctes et en se plaçant dans le repère principal de X on décomposera tout tenseur symétrique Y en deux parties
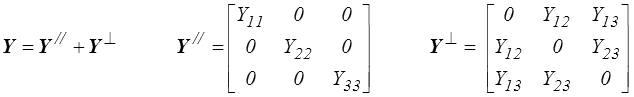
ce qui revient à séparer les composantes diagonales et non diagonales dans le repère principal de X. La partie Y // a les mêmes directions principales et commute donc avec X ou tout tenseur ayant les mêmes directions principales, tandis que la partie Y⊥ lui est orthogonale :
En appliquant cette décomposition à la différentielle dX, il en résulte que les composantes de dX⊥ n'interviendront pas dans la différentiation des invariants. On peut ainsi montrer que
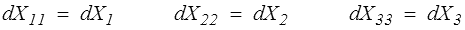
En repère principal de X les composantes diagonales dX // de dX sont les différentielles des valeurs propres de X tandis que les composantes non diagonales dX⊥ définissent la rotation du repère principal.
Il conviendrait aussi de traiter séparément le cas des valeurs propres non toutes distinctes.
Revenant à notre calcul initial, on peut maintenant écrire
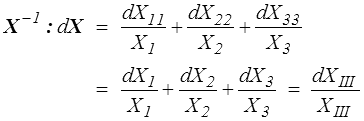
soit finalement ce que nous avait suggéré le calcul en repère principal.
Une application analogue concerne la trace d'une fonction de X obtenue à partir d'une fonction réelle f différentiable. On a en effet en notant f ( X ) la fonction tensorielle généralisant la fonction réelle
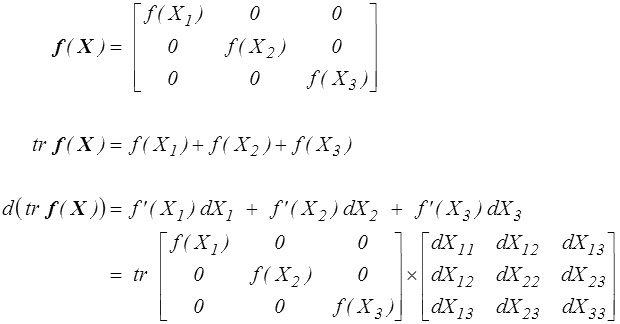
et donc finalement
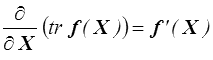
où f ' est la fonction tensorielle généralisant la dérivée f ' de f.
Appliquée à la fonction puissance, on étend ainsi à tout réel m la formule obtenue pour m entier positif.
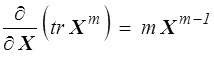
Au-delà du détail de ce paragraphe, assurément très technique, on retiendra surtout que, sans être nécessairement très difficile, la manipulation de ces fonctions tensorielles est souvent plus subtile qu'il n'y paraît et demande précision et précaution.
Théorèmes de représentation
Soit une fonction scalaire isotrope d'un tenseur symétrique A (m-isotrope en fait, mais je fais ici des mathématiques et donc pas de confusion possible, je ne ferai la distinction isotrope vs m-isotrope qu'en cas de risque). On montre alors facilement qu'elle est simplement fonction des 3 invariants fondamentaux
f ( A ) = f ( AI , AII , AIII )
Pour cela il suffit par exemple de remarquer que la fonction matricielle correspondante étant indépendante du repère, on peut se placer en repère principal, et qu'elle ne dépend donc que des valeurs propres ou, ce qui revient au même, des invariants principaux, coefficients de l'équation caractéristique qui donne ces valeurs propres.
On démontre aussi que si X est une fonction isotrope 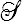→ 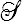alors on peut l'écrire
X ( A ) = αo 1 + α1 A + α2 A2
où αo , α1 et α2 sont des coefficients fonctions des invariants fondamentaux AI , AII et AIII . La démonstration est un peu plus laborieuse : on commence par montrer que tout vecteur propre de A est aussi vecteur propre de X. On se place en repère principal pour obtenir un système de trois équations à trois inconnues qui − au moins dans le cas de valeurs propres distinctes − permet de déterminer αo , α1 et α2 . Il ne reste plus qu'à « nettoyer les coins » (cas de valeurs propres confondues, montrer que les αi ne dépendent que des invariants,...).
Ce sont deux exemples de ce que l'on appelle les « théorèmes de représentation », résultats généraux donnant une forme réduite des fonctions tensorielles isotropes.
Une fonction scalaire dépendra d'un certain nombre d'invariants fondamentaux: par exemple une fonction scalaire isotrope de deux tenseurs symétriques A et B. Elle dépendra alors des invariants fondamentaux de A et B et de 4 invariants mixtes
tr AB tr A2B tr AB2 tr A2B2
On pourra donc écrire (en préférant souvent aux invariants fondamentaux les traces des 3 premières puissances)
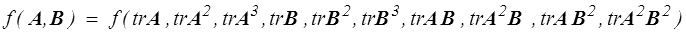
De même une fonction isotrope d'un tenseur symétrique et d'un vecteur pourra s'écrire
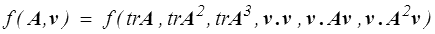
Les démonstrations sont très compliquées, mais on trouvera dans la littérature les listes d'invariants correspondant aux différentes combinaisons de tenseurs et vecteurs (on parle souvent de base d'intégrité).
On remarquera pour la fonction isotrope de 2 tenseurs symétriques que l'on a 10 invariants scalaires, alors que géométriquement 9 auraient dû suffire : les 3 valeurs propres des deux tenseurs et les 3 angles définissant l'orientation relative des deux repères principaux. Il doit donc exister une relation entre ces 10 invariants fondamentaux. Je ne sais pas si on sait l'écrire explicitement, mais en tout état de cause elle ne permet pas de calculer par exemple tr A2B2 en fonction des 9 autres. Une telle relation est appelée syzygie (un terme apparemment emprunté à l'astronomie, mais la relation ne m'apparaît pas évidente !?).
Pour une fonction isotrope tensorielle la forme générale sera une combinaison linéaire d'un certain nombre de générateurs avec des coefficients fonctions scalaires des invariants. Par exemple pour un tenseur symétrique fonction isotrope de deux tenseurs symétriques on peut écrire
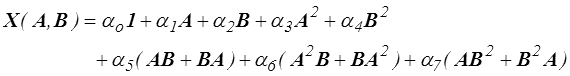
et on trouvera également dans la littérature la liste des générateurs correspondant aux diverses fonctions isotropes tensorielles ou vectorielles.
Quelques exemples
Commençons par deux exemples très simples mais importants par leurs conséquences. Une fonction scalaire isotrope f d'un tenseur symétrique A et d'un vecteur v s'écrira donc
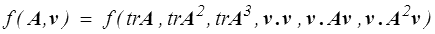
Parmi ces variables
- tr A est linéaire par rapport au couple ( A , v ),
- tr A2 et v . v sont quadratiques,
- les autres sont d'ordre supérieur.
Si cette fonction est quadratique par rapport au couple ( A , v ), elle s'écrira donc
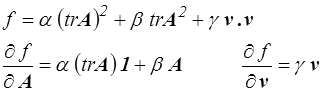
Tenseurs et vecteurs apparaissent donc de manière découplée.
De même un tenseur symétrique X fonction isotrope d'un tenseur symétrique A s'écrit
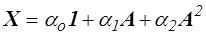
Si cette fonction est linéaire alors α1 est une constante tandis que αo sera fonction linéaire du seul invariant linéaire tr A
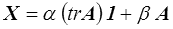
En comparant avec le résultat obtenu plus haut, on remarque que l'on peut considérer que la fonction X s'obtient par dérivation d'une fonction scalaire f et dérive d'un potentiel.
On remarque aussi qu'en prenant pour A et X les tenseurs σ et ε, ceci conduit directement à la loi de Hooke pour un matériau isotrope, l'isotropie du matériau se traduit en l'occurrence par une loi élastique m-isotrope. C'est vrai et assez naturel, mais cela méritera d'être clarifié. L'isotropie d'un matériau et l'isotropie d'une fonction tensorielle (m-isotropie) sont deux notions différentes qu'il est important de ne pas confondre.
Pour un exemple plus sophistiqué, considérons l'équation tensorielle
A X + X A = H
où A est un tenseur symétrique, en général défini positif, et H un tenseur quelconque. On montre facilement, en se plaçant en repère principal de A, que cette équation en A admet une solution unique. Cette solution X ( A , H ) est linéaire en H et fonction isotrope de ses deux arguments A et H. On écrira
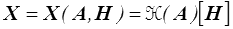
Cet opérateur linéaire 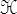( A ) (tenseur du quatrième ordre) apparaît assez régulièrement dans différents calculs. On peut utiliser le théorème de représentation correspondant pour en obtenir une expression explicite : on utilise la solution en repère principal de A pour calculer les coefficients apparaissant dans cette expression. On obtient ainsi
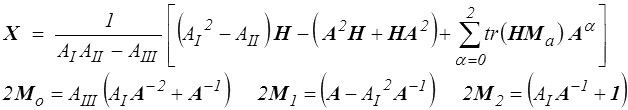
J'avais proposé cette solution en 1978. Curieusement cela reste une de mes publications les plus citées
La fonction exponentielle
La fonction exponentielle d'un tenseur est importante et mérite une attention particulière. Pour un tenseur symétrique, le plus simple est, comme pour toute autre fonction scalaire, de se placer en repère principal, mais pour un tenseur A ∈ 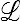quelconque il faut procéder autrement. La définition la plus naturelle part du développement en série classique
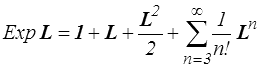
mais il sera souvent commode de l'obtenir par intégration de l'équation différentielle
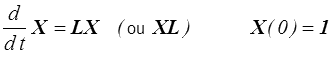
dont la solution est
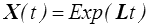
(On remarque simplement que pour tout t cette solution commute avec L , LX = XL ).
L'exponentielle d'un tenseur Ω antisymétrique est une rotation. Pour s'en convaincre on choisit un repère dont l'axe x3 est dans la direction du vecteur adjoint ω (c'est aussi pour Ω la direction propre associée à la valeur propre réelle 0). On pourra donc écrire dans ce repère
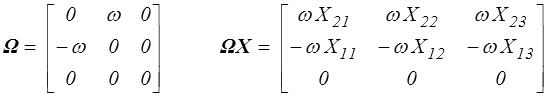
L'équation différentielle pour X = Exp ( Ωt ) devient
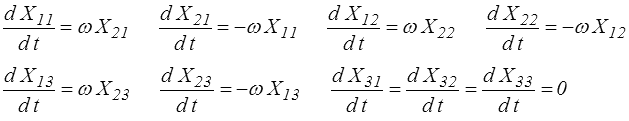
En intégrant les équations de la première ligne on obtient par exemple, avec la condition initiale X (0) = 1,
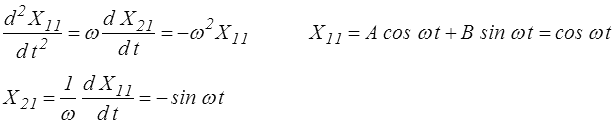
et de même
Les équations de la seconde ligne montrent de même que les autres termes sont nuls. On obtient donc finalement
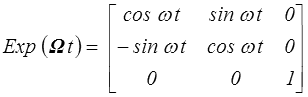
Ainsi l'exponentielle de Ω est une rotation d'angle ω autour de la direction du vecteur ω adjoint de Ω.
On montre également directement
Attention toutefois on ne peut en général pas écrire
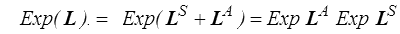
Ceci ne sera vrai que si LS et LA commutent. Plus généralement
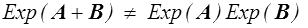
L'égalité ne sera vérifiée que si les deux tenseurs A et B commutent