Mouvement de solide rigide
Transformation de solide rigide
Un mouvement de solide rigide est à chaque instant défini par une rotation Q(t) et une translation c(t)
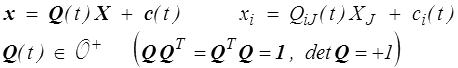
Le tenseur gradient F se réduit alors à la rotation Q
F(t) = Q(t)
Elle ne dépend pas du point considéré (transformation homogène).
Le volume ne change pas (J = 1) tandis que la formule de Nanson se réduit à
n dS = Q N dSo
l'élément de surface suit simplement la rotation.
La transformation relative s'obtient de même
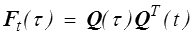
En anticipant sur la suite, on trouvera que toutes les mesures de déformation (>) , (>) sont nulles et que le théorème de décomposition polaire (>) se réduit à
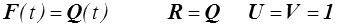
Champ des vitesses
Le champ lagrangien des vitesses s'obtient par dérivation
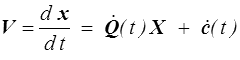
Le champ eulérien d'obtient alors en exprimant X en fonction de x
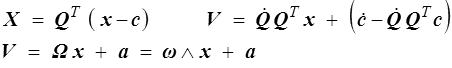
où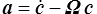 
et où ω est le vecteur adjoint (<)
du tenseur antisymétrique
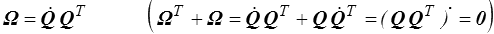
On retrouve donc, bien évidemment, le classique champ rigidifiant (<) − Le tenseur des taux de déformation est nul (<) .
Changement de référentiel
La description du mouvement présuppose le choix d'un référentiel d'observation (<)
. On utilisera par exemple très souvent le « référentiel du laboratoire » (<)
, mais ce n'est pas obligatoire et il est possible d'en changer.
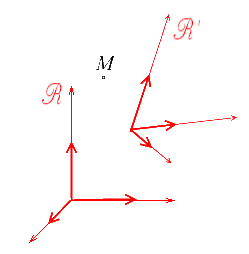
Une fois choisi ce référentiel d'observation, chaque point de l'espace sera à chaque instant repéré par ses trois coordonnées x. Ce même point sera dans un autre référentiel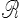 
' repéré par ses 3 nouvelles coordonnées x'. Le changement de référentiel est défini par les relations matricielles reliant les nouvelles coordonnées x' aux anciennes x
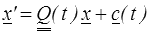
avec une matrice de passage orthogonale Q(t) définissant l'orientation relative des deux repères (orthonormés, toujours).
Comme nous l'avons fait pour les rotations (<) il est possible d'extrapoler cette relation matricielle en une relation tensorielle
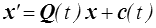
Nous continuerons, par abus de langage, à parler de changement de référentiel, mais il serait plus précis de parler de mouvement de solide rigide : partant d'un mouvement
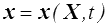
la relation
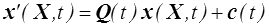
représente un nouveau mouvement obtenu en superposant au mouvement initial un mouvement de solide rigide.
Les tenseurs gradients correspondant à ces deux mouvements sont reliés par
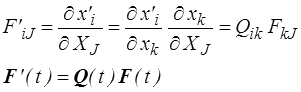
et pour la déformation relative
