Thermodynamique Rationnelle
Ce terme (rational thermodynamics, en anglais) recouvre une approche générale développée dans les années 70 autour de l'Ecole de Truesdell et utilisant la thermodynamique pour la construction de modèles de comportement. Cette appellation peut paraître un peu prétentieuse. Effectivement elle l'est et sa prétendue − et auto-proclamée − rationalité n'a pas vraiment survécu à l'épreuve du temps. Il n'en reste pas moins que, ramenée à ses justes proportions − plus modestes − c'est une approche intéressante et qui mérite considération. De plus, elle pourra nous inciter, nous aussi, à quelque modestie et à prendre conscience que notre approche (TPI, cadre standard généralisé, c'est un peu la marque de fabrique de l'Ecole Française de Mécanique des Matériaux) n'est pas LA thermodynamique mais une approche parmi d'autres, quelles que soient son élégance et son efficacité.
Thermoélasticité
Avant d'aborder des exemples plus novateurs, nous commençons par traiter dans ce cadre les modèles classiques présentés précédemment dans l'environnement TPI (<) . Ceci nous permettra d'une part de mettre en place la méthode et d'autre part de clarifier les différences avec l'approche traditionnelle.
Le point de départ est toujours le second principe de la thermodynamique et l'inégalité de Clausius-Duhem (<)
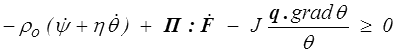
Les lois de comportement permettent alors de calculer toutes les variables dépendantes − à savoir ψ, η, Π et q − en fonction de l'histoire thermocinématique, c'est-à-dire des fonctions x(X,t) et θ(X,t) ainsi que de leurs dérivées spatiales et temporelles.
La première règle − dite d'équiprésence − est de supposer que − a priori et jusqu'à preuve du contraire − ces quatre quantités dépendent de toutes les variables choisies.
Nous choisissons donc au départ une liste de variables, par exemple (F , θ, g = grad θ) et nous postulons
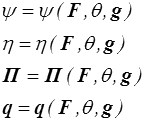
La seconde règle est d'imposer à ces fonctions de vérifier identiquement l'inégalité de Clausius-Duhem pour tout processus thermocinématique. On écrit alors
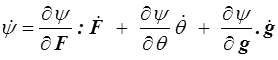
et l'inégalité de Clausius-Duhem devient alors
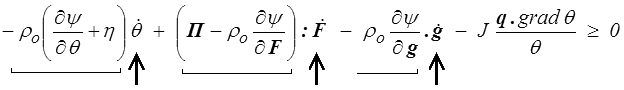
Si l'on fixe F, θ et g, les termes soulignés − qui d'après les lois de comportement en dépendent − sont également fixés, alors que les dérivées d'ordre supérieur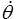 
, 
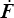et 
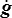(marquées d'une flèche) peuvent être choisies arbitrairement. On en déduit
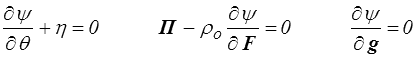
Si par exemple le premier terme souligné n'était pas nul, il suffirait de prendre 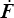et 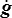nuls et de choisir 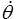de signe opposé et suffisamment grand pour violer l'inégalité.
On en déduit donc
- L'énergie libre ψ, qui aurait pu dépendre du gradient de température (équiprésence), ne peut pas en fait en dépendre.
- L'entropie et le tenseur des contraintes sont donnés par les lois classiques
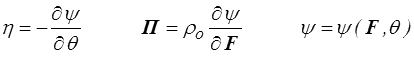
- Reste pour la dissipation
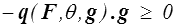
condition à vérifier par la loi de conduction.
On peut aller plus loin en écrivant un développement de Taylor de cette loi autour de g = 0
et l'inégalité de Clausius-Duhem impose alors qo = 0 et un tenseur de conductivité ko semi-défini positif
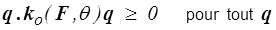
Rien ne lui impose, en particulier, d'être symétrique (en TPI cette symétrie résulte des relations de réciprocité d'Onsager, hypothèse phénoménologique raisonnable et apparemment confortée par l'expérience, mais ce n'est pas une loi thermodynamique).
Modèle de Kelvin-Voigt
Rajoutons maintenant à la liste des variables le tenseur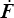
L'inégalité de Clausius-Duhem deviendra alors
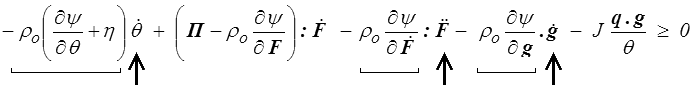
On fixe comme précédemment les variables de base (F, 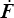,θ, g) et donc les termes soulignés. Les dérivées d'ordre supérieur , 
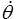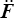et 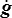pouvant être choisies arbitrairement, les facteurs correspondants doivent s'annuler et on aura donc encore
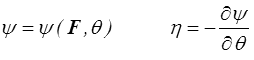
tandis que l'inégalité de dissipation se réduit à
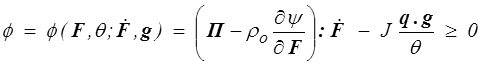
On remarquera que, à la différence de présentation près, on retrouve exactement la même chose que par la démarche classique (<)
, ce qui est à tout le moins rassurant. La thermodynamique rationnelle ignore, ou fait semblant d'ignorer, la distinction, pour nous essentielle, entre les variables d'état thermodynamiques (F, θ) et les forces et flux thermodynamiques (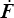 et g). Mais cette distinction arrive ensuite naturellement. Par contre une fois obtenue cette expression de la dissipation et analysées ses conséquences, la thermodynamique rationnelle arrive à son terme.
L'inégalité de dissipation
Pour analyser de manière plus générale la condition de dissipation il sera commode de distinguer ces deux types de variables en écrivant
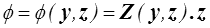
- y = (F,θ) variables d'état
- z = (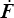,g) flux / forces en description mixte (<)
La dissipation est évidemment nulle à l'équilibre (z = 0). Au voisinage de l'équilibre, on peut alors développer la fonction Z(y, z) (supposée suffisamment régulière)
L'inégalité de dissipation devient alors
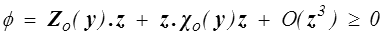
qui impose naturellement
Le vecteur Zo(y) est nul et l'application linéaire χo(y) est semi-définie positive. Ces conditions nécessaires sont également suffisantes si on se limite au modèle linéaire.
Ces conditions sont bien moins fortes que celles imposées sur χo par les relations de réciprocité de Casimir-Onsager (<) .
Appliquées au modèle de Kelvin-Voigt cela donne pour un modèle linéaire
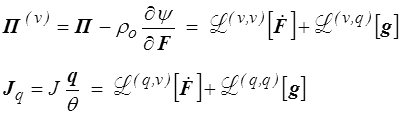
avec des tenseurs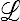 
du second (q,q), troisième (v,q) et (q,v) et quatrième (v,v) ordre, fonctions des variables d'état et définissant une forme quadratique semi-définie positive. Les relations de symétrie de Casimir-Onsager imposeraient de plus (<)
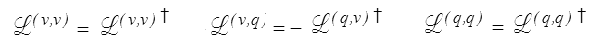
Insistons à nouveau sur le fait que notre approche (variables internes + TPI) n'est pas la seule possible.
Milieux à deux températures ===>
A titre d'exemple, le modèle d'un milieu à double températures est particulièrement instructif.