Glissement, extension cisaillement
Glissement simple
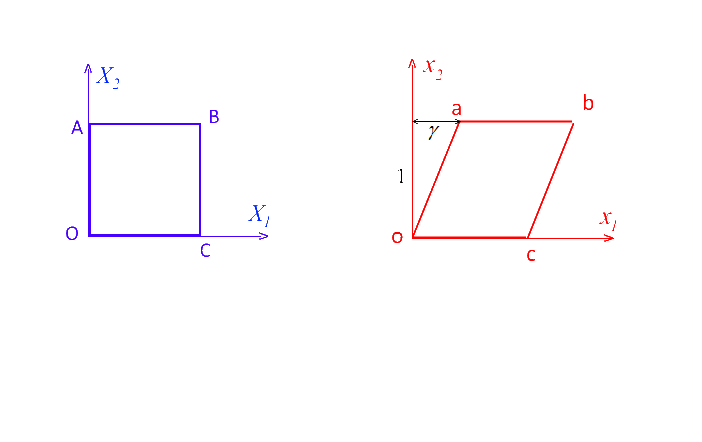Un mouvement de glissement simple est défini par
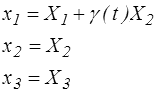
Le tenseur gradient et son inverse sont
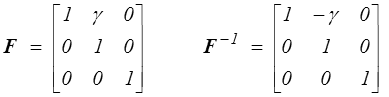
Le tenseur de Cauchy-Green droit C et le tenseur des déformations de Green-Lagrange s'obtiennent directement
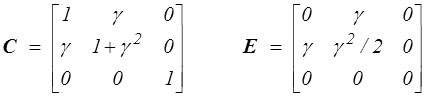
Le terme E22 correspond à l'allongement du vecteur matériel OA dans la direction x2 c'est-à-dire à la variation de longueur oa/OA. C'est pour γ petit un terme du second ordre qui n'apparaissait donc pas en petites perturbations (<) . C'est un exemple typique des non linéarités géométriques induites par les grandes transformations. On peut s'attendre à ce que cet allongement engendre en glissement simple des contraintes normales σ11 et σ22 . Effectivement l'apparition de ces contraintes normales est une des manifestations les plus spectaculaires des effets de grandes déformations.
On montrera plus tard que le tenseur des contraintes de Cauchy a, pour un milieu isotrope, la forme suivante
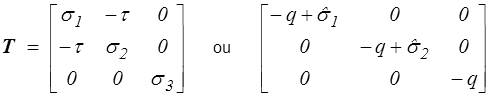
selon que le matériau est compressible ou incompressible. Dans ce dernier cadre en effet, très courant en grandes transformations rappelons-le, les contraintes ne seront déterminées qu'à une pression hydrostatique près.
Glissement simple stationnaire
Les tenseurs gradient des vitesses, taux de rotation et taux de déformation sont respectivement donnés par
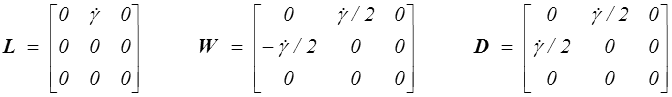
Le glissement simple stationnaire correspond au cas où la vitesse de glissement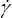 
est constante
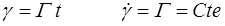
Le tenseur gradient des vitesses reste constant. C'est l'écoulement de référence en mécanique des fluides. Pour un fluide visqueux newtonien (incompressible) il vient par exemple
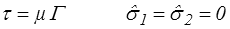
Outre son importance pratique, cet écoulement présente quelques propriétés remarquables plus ou moins liées au fait que, L étant constant, la fonction F(t) est une exponentielle (<)
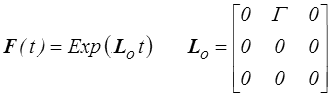
On calcule en particulier la déformation relative (<)
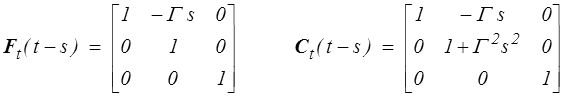
On parlera plus tard d'un mouvement à histoire de déformation constante (motion with constant stretch history). Cette structure que le glissement simple stationnaire partage avec les mouvements ρ-extensométriques (<) (mais ce sont à peu de choses près les seuls) impliquent d'intéressantes conséquences qui joueront plus tard un rôle essentiel en mécanique des fluides.
Allongements, glissements, rotation
La forme obtenue plus haut pour le tenseur des déformations de Green-Lagrange montre que l'allongement E22, négligeable pour Γ petit, augmente ensuite rapidement et devient même prépondérant pour Γ grand.
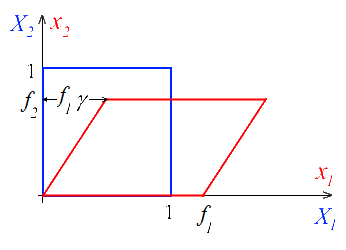
Ceci est illustré sur la figure ci-contre qui représente la déformation pour γ = 1 et γ = π. Elle montre bien que pour γ grand un « glissement » ressemble autant à une traction qu'à un cisaillement.
Pour quantifier cela, et par la même occasion à titre d'exercice, on peut calculer les allongements et rotation en effectuant la décomposition polaire du tenseur F.
Les valeurs propres du tenseur C s'obtiennent en résolvant son équation caractéristique
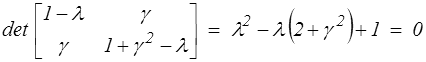
soit, par résolution de cette équation du second degré,
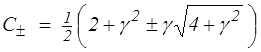
On en déduit les allongements principaux et les déformations logarithmiques principales
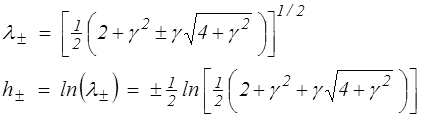
Pour la rotation, il faut déterminer la direction principale correspondant par exemple à la valeur propre C+. Soit (u1 ,u2 ) un vecteur propre et θu l'angle formé par ce vecteur avec la direction x1, il vient
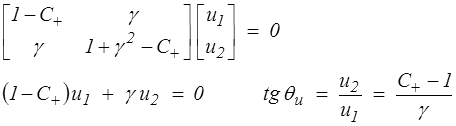
et on obtient finalement
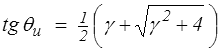
Il faut ensuite faire le même calcul sur le tenseur de Cauchy-Green gauche B
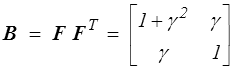
On obtient bien évidemment les mêmes valeurs propres et pour l'orientation θv
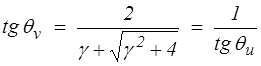
Les directions principales de C et B sont symétriques par rapport à la première bissectrice. On trouvera ci-dessous les courbes donnant h+ et la rotation propre θ = θv − θu en fonction de γ. La droite noire correspond à l'approximation HPP (θ = h+ = γ/2) et la droite horizontale rouge à l'asymptote θ = π/2 obtenue pour γ → ∞.
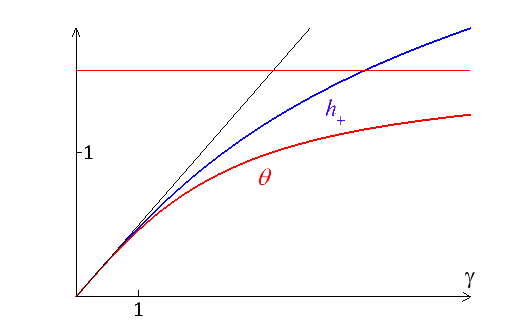
Il pourra aussi être intéressant de se reporter à l'animation (>). C'est un bon exemple pour l'expérimenter.
Extension - Cisaillement
On a vu que le glissement simple s'accompagnait, en grandes transformations, d'allongements, ce qui laisse prévoir des couplages entre contraintes de cisaillement et contraintes normales. On peut donc aussi s'attendre à des couplages similaires lors d'essais mécaniques de ce type (<). Il sera alors souvent utile de considérer le mouvement d'extension cisaillement défini par
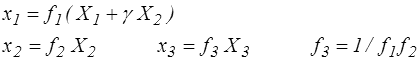
en nous limitant désormais au cas incompressible.
Les tenseurs F et F −1 sont alors
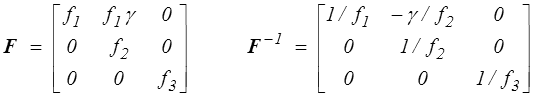
Le tenseur gradient des vitesses est alors
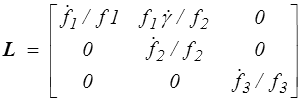
comme pour le mouvement ρ-extensométrique (<) le tenseur des contraintes aura la forme
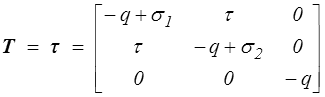
avec, par exemple en contraintes planes (<) , q = σ33 = 0.
La puissance des efforts intérieurs (>) sera alors
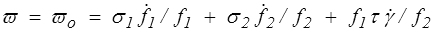
et on peut prévoir que la loi de comportement conduira à une relation entre les contraintes σ1, σ2 et τ et les paramètres de déformation que sont f1, f2 et γ.
Exemples d'application
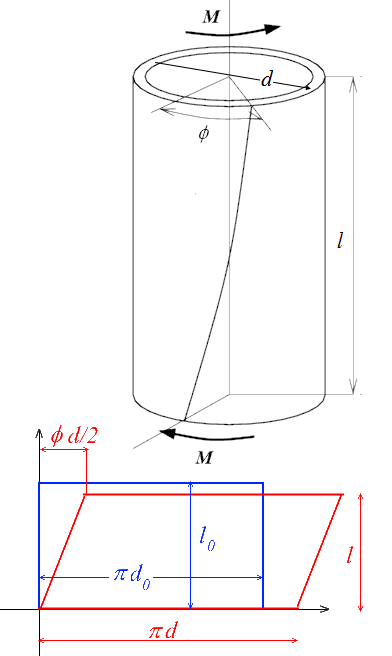Considérons l'essai de traction-torsion d'un tube mince (<).
. Soient lo, do et eo [resp. l, d et e] la longueur, le diamètre et l'épaisseur initiales [resp. après déformation] du tube et on note également ϕ la rotation de la face supérieure.
Dans le repère local (eθ ,ez ,er ) le tenseur gradient est représenté ci-contre et pourra s'écrire
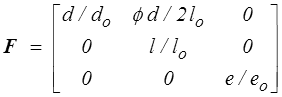
qui est bien de la forme étudiée plus haut avec
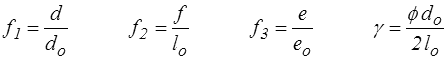
Quant au tenseur des contraintes de Cauchy il s'écrira, dans le même repère,
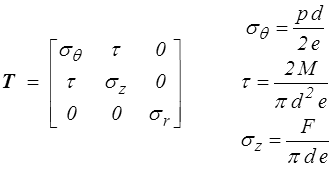
en fonction du couple de torsion M, de l'effort axial F et d'une éventuelle pression interne p. Nous n'avons eu ici qu'à reprendre les résultats déjà obtenus dans l'analyse de cet essai (<). On notera simplement que l'analyse statique qui a permis de les obtenir doit être menée dans la configuration actuelle où a lieu l'équilibre et que ces formules doivent donc faire intervenir les grandeurs géométriques eulériennes d et e (et non do et eo ).
Rappelons toutefois que cet essai n'est malheureusement pas vraiment utilisable car il conduit rapidement, comme nous l'avons déjà évoqué en HPP, à un phénomène de flambement. L'essai de torsion d'un arbre plein est par contre utilisable et permet effectivement d'engendrer de très grandes déformations, mais son analyse est bien plus complexe puisqu'il s'agit d'un essai non homogène. Les résultats précédents ne restent valables que localement et on ne peut pas évaluer directement les contraintes en fonction des efforts appliqués.
Une autre application importante de l'extension cisaillement est la traction hors axe : lorsqu'un matériau anisotrope est soumis à un essai de traction dans une direction inclinée par rapport aux axes de symétrie du matériau, l'allongement longitudinal s'accompagne comme toujours d'une contraction transversale mais aussi d'une rotation des sections d'extrémités. C'est donc encore un mouvement d'extension cisaillement et on peut s'attendre à ce que les conditions σ2 = τ = 0 permettent de déterminer en fonction de l'allongement longitudinal f1, la contraction transversale f2 et le glissement γ.
