Un premier exemple
Loi de Hooke en grandes transformations
La loi de Hooke (<) , modèle de base de mécanique des solides HPP, s'écrivait
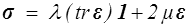
Pour étendre ce modèle aux grandes transformations le plus simple est de conserver cette forme en remplaçant σ et ε par l'un ou l'autre des différents tenseurs que nous venons d'introduire pour décrire les contraintes et les déformations.
Nous écrirons donc formellement
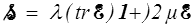
ou sous forme inverse inverse (<)
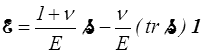
où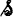 
et 
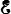sont deux tenseurs grandes transformations choisis parmi ceux que nous avons définis précédemment. Mais comment choisir ?
Pour les contraintes nous avons pour l'instant introduit 4 tenseurs (<) T, τ, Π et S, qui tous redonnent en HPP le tenseur usuel σ. Toutefois le tenseur Π (PK1) est non symétrique et nous l'excluons de la liste des candidats potentiels.
Pour les déformations nous avons d'abord introduit les tenseurs de Green-Lagrange E et d'Euler-Almansi A (<) , puis ensuite étendu la liste aux mesures de Seth-Hill E(m) et e(m) (<) , avec une mention particulière pour les tenseurs de Hencky H et h (<) . Là encore tous se réduisent en HPP au tenseur des déformations infinitésimales ε.
Il semble ensuite naturel de ne pas mélanger les couleurs et d'exclure par exemple l'écriture
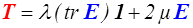
reliant un tenseur eulérien T (rouge) à un tenseur lagrangien E (bleu). On choisira donc une écriture lagrangienne − bleue − par exemple
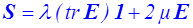
ou eulérienne − rouge − par exemple
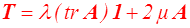
Traction simple
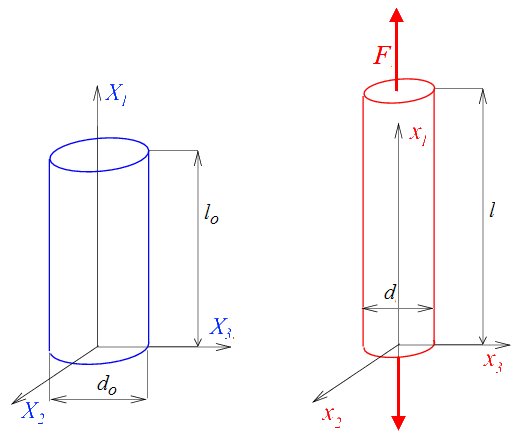Dans un essai de traction simple (<)
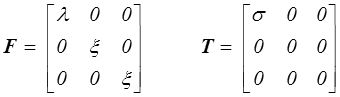
avec λ = l/lo , ξ = d/do , σ = F/S.
On obtient directement pour les déformations
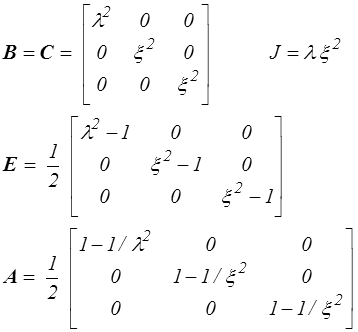
et pour les contraintes
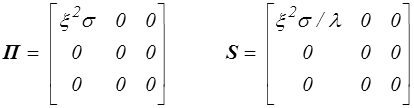
Quel que soit le tenseur choisi pour on constate que seule la composante 
11 est non nulle. La loi de Hooke donnera alors directement
La première relation permettra, selon le choix fait, de calculer la contraction ξ en fonction de l'allongement λ. La contrainte σ s'obtiendra ensuite en reportant dans la seconde équation.
En choisissant l'écriture lagrangienne, relation entre S et E (PK2 et Green-Lagrange) on obtient ainsi
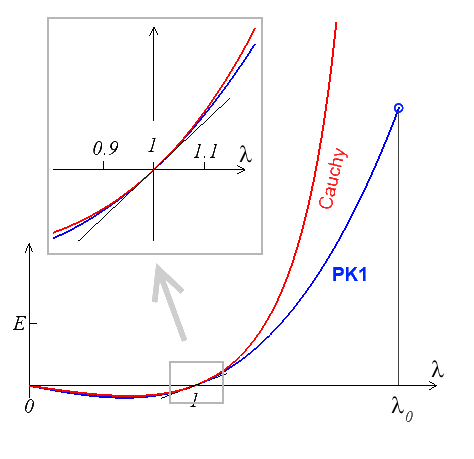
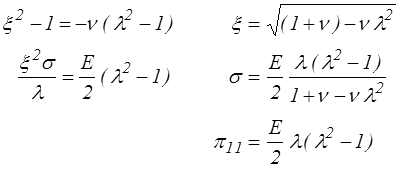
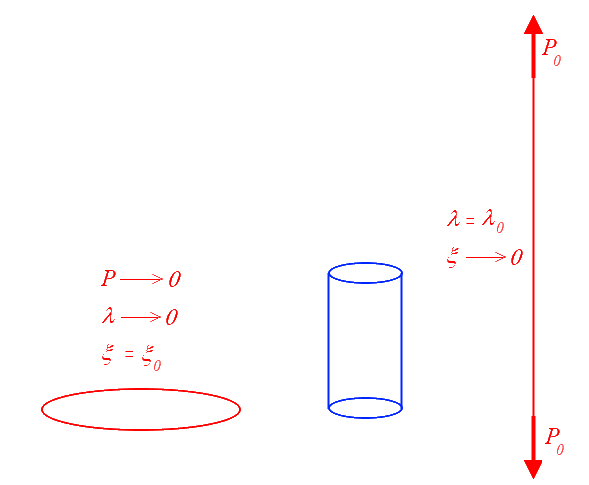
Les courbes correspondantes sont représentées ci-contre pour ν = 0.25.
On constate que
ξ → 0 pour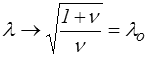 
et que
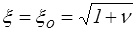pour λ = 0 , σ → 0
Ce comportement est
- bizarre en traction, puisque l'allongement longitudinal est limité à λo sous contrainte infinie mais force finie.
- complètement aberrant en compression, puisqu'une éprouvette s'écrase complètement sous force et contrainte nulles.
En choisissant l'approche eulérienne, relation entre T et A (Cauchy et Euler-Almansi), on obtient de même
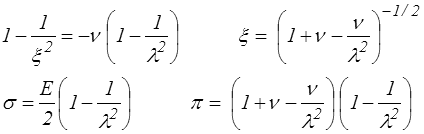
On constate là encore un comportement inacceptable puisque
- en traction
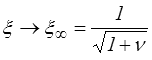pour λ → ∞ - en compression ξ → ∞ pour
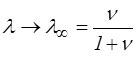
Construire une loi de Hooke complètement raisonnable en grandes transformations, c'était semble-t-il un projet bien modeste. Ce n'est en fait pas si simple.
Choix de la déformation
A y regarder de plus près, les difficultés que nous avons rencontrées résultent essentiellement de la relation entre ξ et λ, c'est-à-dire du choix fait pour le tenseur des déformations. Elargissons le choix en considérant les mesures de Seth-Hill E(m) = e(m) puisque, en traction simple, R = 1. On aura alors en traction simple pour m ≠ 0
de sorte que la loi de Hooke donnera
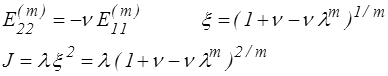
Pour m = 0 (tenseur de Hencky) on obtient de même
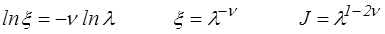
On constate ainsi que
- pour m > 0
- pour m < 0
- Seul le cas m = 0 conduit à un comportement raisonnable
ξ → 0 et J → ∞ pour λ → ∞
ξ → ∞ et J → 0 pour λ → 0
dans le cas compressible (ν < 1/2), tandis que dans le cas incompressible, ν = 1/2, il vient simplement
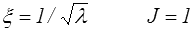
ξ → 0 et J → 0 pour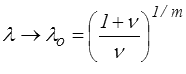 
λ → 0 et J → 0 pour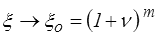 
ξ → ∞ et J → ∞ pour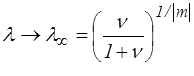 
λ → ∞ et J → ∞ pour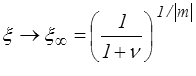 
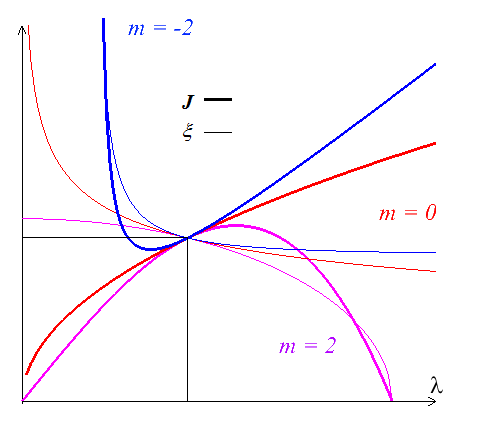
La figure ci-dessous montre les courbes correspondantes (ν < 0.25) donnant ξ (trait fin) et J (trait épais) pour
m = 2 (Green-Lagrange, magenta)
m = 0 ((Hencky, rouge)
m = − 2 (Euler-Almansi, bleu)
On aurait également pu remarquer directement que la loi de Hooke pouvant aussi s'écrire
il fallait utiliser une mesure de déformation telle que sa décomposition en partie sphérique et déviateur décrive la dilatation sphérique et la distorsion. Seul le tenseur de Hencky satisfait cette condition.
Une loi de Hooke
Nous devons donc, pour obtenir un comportement raisonnable, choisir comme déformation le tenseur de Hencky H et h. Reste à choisir le tenseur des contraintes : S, τ ou T. Le comportement correspondant s'obtient directement en écrivant
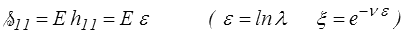
ce qui, suivant le choix fait, donnera pour σ = F/S,
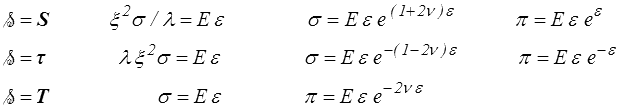
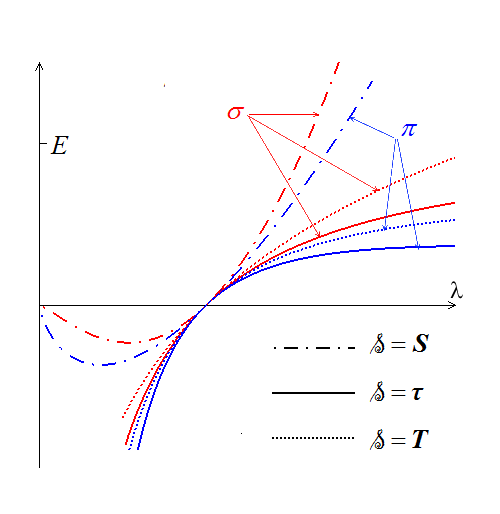
Les courbes correspondantes sont représentées ci-contre pour ν = 0.3 . Le choix de S est inacceptable (force et contrainte nulles pour λ → 0 , ξ → ∞ ). Il est par contre difficile de trancher entre les deux tenseurs eulériens τ et T. Des considérations thermodynamiques nous conduirons plus tard à choisir τ plutôt que T. Nous retenons donc la forme
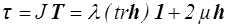
On constate en particulier que les deux courbes π(ε) et σ(ε) ont toutes deux un maximum respectivement pour ε = 1 et (1 − 2ν) − 1.
Pour la première c'est normal : la diminution de la section peut compenser l'augmentation de la contrainte, c'est le phénomène de striction (<) . Pour la seconde c'est plus étonnant, mais il n'y a pas de raison fondamentale d'exclure une telle possibilité. De plus, cela ne pourrait intervenir QUE pour de très grandes déformations, bien au-delà de ce que l'on peut imposer dans un essai de traction. Remarquons aussi que cette éventualité disparaît dans le cas incompressible ν = 1/2 , hypothèse qui sera très souvent faite en grandes transformations − nous y reviendrons.
Conclusion provisoire
Je ne saurais trop recommander aux néophytes de refaire ces quelques calculs, tout à fait représentatifs des grandes transformations. N'hésitez d'ailleurs pas à me signaler toute erreur de calcul ou de transcription. J'ai essayé de faire cela avec soin, mais une erreur est vite arrivée. Je suis sûr de mes conclusions mais un peu moins du détail des calculs.
Toutefois et pour instructifs qu'ils soient, leur intérêt dépasse le simple exercice et nous pouvons en tirer quelques enseignements de portée beaucoup plus générale:
- L'écriture d'une loi de comportement complètement cohérente en grandes transformations n'est pas aussi simple que l'on aurait pu le croire. La traction simple est déjà un test révélateur.
- Dans le doute et si l'on veut faire simple, l'utilisation des déformations logarithmiques, permet de minimiser les risques.
- Une prise en compte correcte de la compressibilité et des variations de volume est cruciale et l'hypothèse d'incompressiblité est commode.