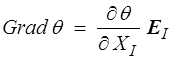Le second principe
Production interne d'entropie
Le second principe introduit deux nouvelles fonctions d'état, l'entropie S et la température absolue que nous noterons désormais θ (pour éviter la confusion avec le tenseur des contraintes de Cauchy T).
- La température θ, variable intensive, devient une fonction de la position x et du temps (champ de température).
- L'entropie S, variable extensive, s'exprime, comme l'énergie interne, à partir de l'entropie spécifique η (entropie par unité de masse)
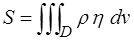
Le second principe s'écrira alors
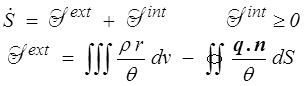
où l'apport extérieur d'entropie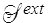 
est une extension naturelle du
đ Q / T de la thermodynamique classique (<)
pour notre modélisation des échanges de chaleur. Le second principe s'écrit donc
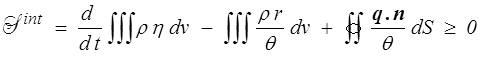
L'irréversibilité se traduit par une production interne d'entropie positive (non-conservation de l'entropie)
Inégalité de Clausius-Duhem
Le théorème de la divergence et le théorème de Reynolds permettent de transformer cette inégalité en
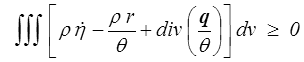
ou, puisque cette inégalité doit être vérifiée pour tout domaine matériel,
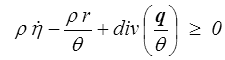
mais
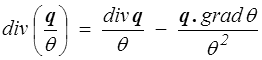
petit exercice facile d'analyse vectorielle (<) .
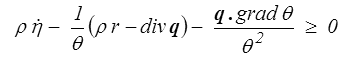
soit finalement, en utilisant la conservation de l'énergie et en multipliant par θ,
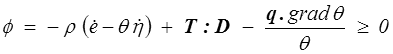
première forme de l'inégalité de Clausius-Duhem à laquelle on préfère habituellement la seconde forme obtenue en remplaçant l'énergie interne e par l'énergie libre ψ
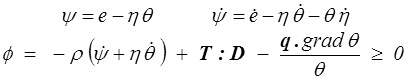
C'est cette inégalité que l'on utilise habituellement comme l'expression du second principe de la thermodynamique en MMC.
Bien que traditionnelle cette formulation est critiquable ; il semblerait notamment qu'elle autorise des mouvements perpétuels de seconde espèce, qui sont, en thermodynamique, strictement interdits. Il existe en fait des modèles plus raffinés pour la thermodynamique des milieux continus. Nous en montrerons un exemple plus loin (>) , mais nous nous limiterons dans ce cours à cette formulation traditionnelle et largement suffisante pour les applications.
Dissipation thermique
Une première source de dissipation est la dissipation thermique
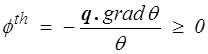
Elle sera pratiquement toujours présente et ne pourra disparaître que dans deux cas limites
- milieu thermiquement isolant q = 0,
- milieu parfaitement conducteur grad θ = 0, θ = C te.
On la supposera souvent découplée des autres sources de dissipation, et on écrira simplement les relations d'Onsager (<) avec par exemple
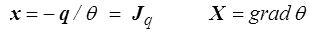
ce qui conduit directement à la loi de Fourier
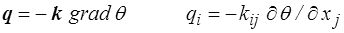
Dans le cas d'un milieu continu non déformable − qui peut le plus peut le moins − l'équation de conservation de l'énergie se réduira alors simplement à
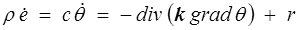
où c = ρ de / dθ est la chaleur spécifique (l'énergie interne ne dépend alors que de la température).
Dans le cas isotrope homogène, on obtient ainsi la classique équation de la chaleur
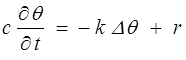
Dissipation intrinsèque
La dissipation intrinsèque correspond au terme restant dans la dissipation
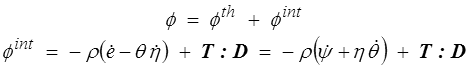
C'est lui qui nous intéressera dans la suite. Le second principe ne lui impose pas d'être positif : seule la dissipation totale doit l'être, et on peut imaginer des situations de couplage où l'une de ces deux dissipations est négative. Nous discuterons plus loin cette question, mais ce sont des cas d'école et on admettra en général que la dissipation thermique et la dissipation intrinsèque sont découplées et donc toutes deux positives.
Pour aller plus loin il faudra caractériser les variables (locales) d'état. Ce seront
- les variables issues du modèle proto-thermodynamique. Nous les noterons symboliquement y, sans préciser davantage. Ce seront souvent des variables tensorielles − notamment les déformations − et il faudra sans doute prendre quelques précautions pour les dériver. Les développements qui suivent seront donc assez largement formels et devront être précisés dans la suite.
- la variable spécifiquement thermodynamique : l'entropie η pour l'énergie interne e ou la température θ pour l'énergie libre ψ (<) .
Nous écrirons donc
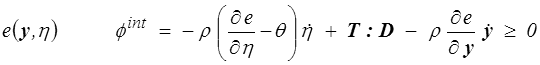
soit, en supposant nulle la dissipation entropique (<) ,
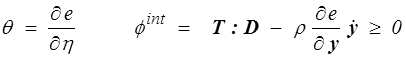
On préfèrera toutefois en général utiliser l'énergie libre
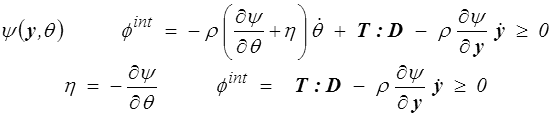
Equation de la chaleur
Sous forme locale le premier principe s'écrivait finalement (<)
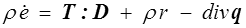
En combinant cette équation avec la définition de la dissipation intrinsèque on obtient
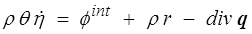
La dissipation intrinsèque représente, à côté de l'apport extérieur ρ r, une production intérieure de chaleur: elle correspond à l'énergie mécanique dégradée en chaleur. C'est bien cela qui nous avait servi de point de départ pour le bilan énergétique de base en mécanique des matériaux (<).
Pour aller plus loin on remarque que
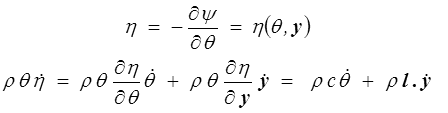
où c est la chaleur spécifique (à y constant) et où l généralise les coefficients calorimétriques de la thermodynamique classique. On obtient donc finalement l'équation de l'énergie sous la forme
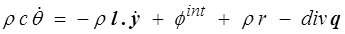
qui, complétée par la loi de Fourier, donnera l'équation de la chaleur généralisée pour un milieu continu. Par rapport à l'équation de la chaleur usuelle, il faut rajouter
- la convection due au terme convectif dans la dérivée particulaire
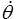, - les termes associés aux coefficients calorimétriques.
- la dissipation intrinsèque qui intervient comme un terme source.
Formulation lagrangienne
Comme pour le premier principe on peut mettre en place une formulation lagrangienne qui, finalement, se traduira simplement par l'expression lagrangienne de la dissipation intrinsèque
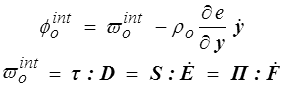
où ϖo int est la puissance des efforts intérieurs par unité de volume dans Co.
Plus généralement, et en introduisant le flux de chaleur lagrangien Q (<) , nous pouvons écrire la dissipation ϕo (production interne d'entropie par unité de volume dans Co)
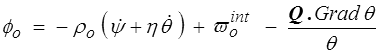
où Grad θ est le gradient de température lagrangien
