Grandes Transformations
Description de la transformation ==>>
L'hypothèse des petites perturbations (<) nous avait permis d'identifier les variables de Lagrange et d'Euler, et donc d'identifier la variable d'espace x (eulérienne) à la variable lagrangienne X attachée à chaque particule. On pouvait alors interpréter la variable x comme lagrangienne (par exemple pour le calcul des dérivées temporelles) ou eulérienne (par exemple pour écrire les lois de la physique) selon ce qui nous arrangeait.
Cette approximation n'est pas toujours permise
- le plus souvent parce que les déformations sont effectivement importantes (fluides, fluage, mise en forme,...)
- mais aussi parfois parce que de petites déformations peuvent induire de grands déplacements (c'est notamment le cas dans les poutres ou les plaques).
Deux voies s'ouvrent alors : on peut choisir de privilégier l'une des deux, mais il faut alors assumer les conséquences de ce choix. C'est par exemple ce que fait le mécanicien des fluides en utilisant la description eulérienne, mais le prix à payer est lourd : dérivées particulaires, terme non linéaire dans les équations de Navier-Stokes.
Il est en fait plus simple d'accepter cette double description en tirant profit de leurs avantages respectifs. Mais il faut alors maîtriser parfaitement leur relation et savoir passer de l'une à l'autre. L'outil de base pour ce passage est le tenseur gradient de déformation.
Ceci nous permettra également d'introduire les notations tensorielles intrinsèques ===> qui, dans ce cours, se substitueront en général aux notations indicielles (<) qui deviendraient ici trop lourdes.
Contraintes ==>>
La première étape est alors l'écriture de la loi fondamentale, loi eulérienne puisque écrite dans l'espace physique, c'est-à-dire dans la configuration actuelle. Le postulat de Cauchy permet alors de décrire le vecteur contrainte comme force (eulérienne par essence) par unité de surface actuelle donc eulérienne, mais on peut aussi choisir de la rapporter à la configuration de référence lagrangienne. Ceci conduit à introduire, à côté de l'habituel tenseur des contraintes de Cauchy T , le premier tenseur de Piola-Kirchoff Π plus déroutant au premier abord (notamment car en général non symétrique) mais néanmoins porteur de sens physique. D'autres tenseurs peuvent également être introduits, en particulier le second tenseur de Piola-Kirchoff S et le tenseur de Kirchoff τ, qui peuvent être utiles mais n'ont pas de signification physique directe.
Exemples et applications ==>>
Nous aborderons alors trois exemples représentatifs dont nous poursuivrons ensuite le développement tout au long de ce chapitre :
- Mouvement de solide rigide,
- Mouvement triaxial,
- Glissement et extension-cisaillement.
Déformations ==>>
Nous nous intéresserons ensuite aux déformations que nous caractériserons géométriquement. Deux voies peuvent être suivies :
- Partir des variations de longueur et d'angle (allongements et glissements), ce qui nous conduira à deux tenseurs de déformation, Green-Lagrange E et Euler-Almansi A.
- Utiliser le théorème de décomposition polaire qui nous donnera une autre représentation, sans doute plus parlante, de la transformation en déformation et rotation.
Nous généraliserons ensuite en introduisant les mesures de Seth-Hill et notamment le tenseur de Hencky des déformations logarithmiques.
Dans le cas bidimensionnel on peut aller beaucoup plus loin, et notamment généraliser le cercle de Mohr des transformations en un cercloïde de Mohr (développement à ma connaissance original, mais que je n'ai jamais osé publier).
Après avoir défini contraintes et déformations, il est tentant de les mettre en relation pour écrire une loi de Hooke généralisée. Ce sera du bricolage, mais très instructif et révélateur des difficultés spécifiques aux grandes transformations.
Dualité contraintes-déformations ==>>
Le lecteur malicieux se sera peut-être aperçu que j'ai utilisé l'approche courante qui consiste à construire géométriquement les déformations indépendamment des contraintes. Or j'avais justement récusé cette approche en petites perturbations (<) . La raison en est qu'ici la dualité naturelle est la dualité contraintes-vitesses de déformations tandis que le passage aux déformations elles-mêmes n'est pas simple.
Partant alors du théorème des puissances virtuelles, nous pourrons sans difficulté construire les vitesses de déformation associées mais la relation entre ces vitesses de déformation et les tenseurs de déformation introduits plus haut sera, sauf en description complètement lagrangienne, beaucoup plus complexe, trop complexe en fait pour être abordée maintenant. Il faudra y revenir.
Équations constitutives ==>>
Comme en HPP, après avoir défini contraintes et déformations, reste à écrire la loi de comportement, ou équation constitutive, reliant les unes aux autres. Nous savons déjà que, pour prendre en compte la mémoire du matériau, cette relation s'exprimera par une fonctionnelle héréditaire causale (<) .
Nous partirons donc d'une loi
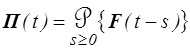
donnant ici le tenseur PK1 à l'instant t comme fonction de l'histoire du gradient de déformation. C'est une écriture formelle car trop générale mais, échaudés par nos déboires pour l'écriture d'une simple loi de Hooke (<) , nous nous méfions désormais de tout choix prématuré. Avec cette écriture nous ne nous engageons certes pas beaucoup mais nous n'hypothéquons pas l'avenir.
Pour formelle qu'elle soit, cette écriture nous permettra toutefois de dégager quelques principes généraux importants et une typologie basique des modèles. Nous évoquerons alors les trois idées qui nous permettront plus tard de finaliser :
- Prise en compte des liaisons internes (incompressibilité),
- Indifférence matérielle,
- Symétries matérielles.
Coordonnées matérielles ==>>
Nous consacrerons un paragraphe à l'utilisation des coordonnées matérielles (c'est-à-dire lagrangiennes) dans la configuration actuelle (c'est-à-dire eulérienne). C'est une approche alternative largement utilisée, notamment dans la littérature. Elle est assurément pertinente, notamment en mécanique des solides (pour les fluides, je suis plus circonspect). Elle est au final bien évidemment équivalente à celle que nous avons utilisé, mais elle oblige à utiliser des coordonnées curvilignes, ce qui alourdit significativement l'environnement mathématique.
