Transformation triaxiale
Définition
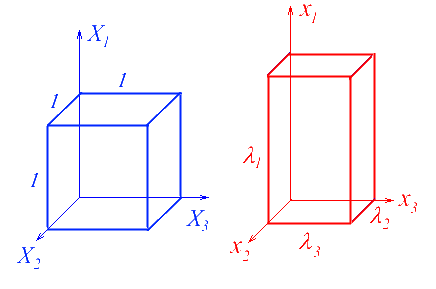Un mouvement triaxial homogène est simplement défini par
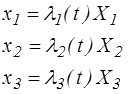
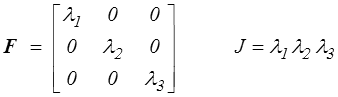
où λ1, λ2 et λ3 sont des constantes (par rapport à X, elles peuvent évidemment dépendre du temps). Le tenseur gradient sera alors
Pour un mouvement non homogène on pourra retrouver cette situation en certains points (mouvement localement triaxial). L'essentiel de ce que nous allons voir restera alors localement valable, mais ce sont des cas marginaux sans grande importance.
Contraintes
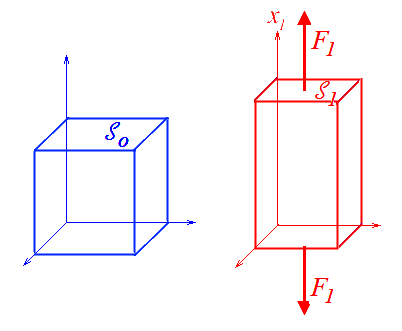Pour un matériau isotrope, et par raison de symétrie, le tenseur des contraintes de Cauchy T sera lui aussi diagonal
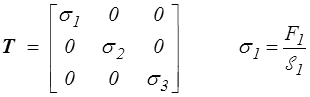
Cette propriété est en fait démontrable (mais il nous faudra au préalable définir l'isotropie, écrire une loi de comportement, etc...). Elle est toutefois bien naturelle et nous l'accepterons. La contrainte de Cauchy σ1 par exemple s'obtient en rapportant la force F1 à la section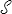 
1 normale à la direction x1 et sur laquelle elle s'exerce.
En notant 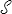o la surface correspondante dans la configuration de référence, on aura naturellement
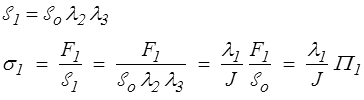
où la contrainte Π1 = F1 /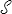o rapporte la force F1 à la section initiale 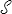o. C'est la composante 1 du premier tenseur de Piola-Kirchhoff, en accord bien sûr avec la relation reliant ces deux tenseurs (<)
. Les autres tenseurs de contraintes, PK2 et Kirchhoff par exemple, seront également diagonaux et on aura par exemple (<)
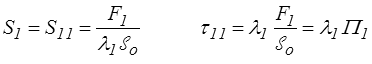
Déformations
En avançant dans le cours nous allons définir plusieurs tenseurs de déformation (>) . Ils seront tous diagonaux et on obtiendra par exemple pour les tenseurs de Green-Lagrange (>) , Euler-Almansi (>) et Hencky (>)
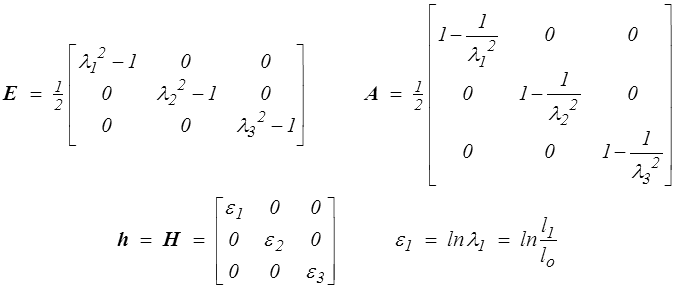
Il n'y a pas de rotation et le théorème de décomposition polaire (>) s'écrit simplement
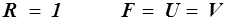
Plus généralement, les déformations de Seth-Hill (>) seront définies par
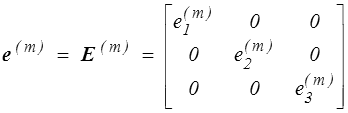
avec
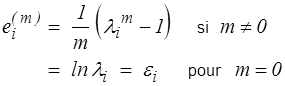
Puissance des efforts intérieurs
La puissance des efforts intérieurs a été introduite en MMC (<) et nous y reviendrons bientôt dans le cas général (>) . Mais on peut ici l'obtenir très simplement.
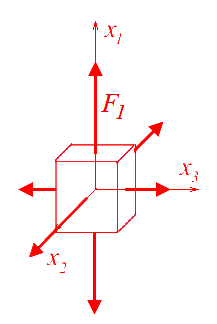Pour travailler par unité de volume dans Co nous partons d'un cube de côté lo qui devient après déformation un parallélépipède rectangle de côtés l1, l2, l3 (li = lo λi ). Notant F1, F2, F3 les efforts exercés sur les faces respectivement normales à x1, x2 et x3, le travail de ces efforts dans un mouvement virtuel sera
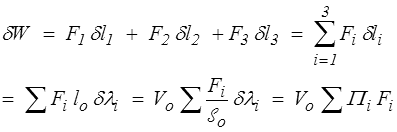
en introduisant les composantes du tenseur PK1 Πi = Fi /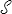o , 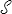o = lo2, Vo = lo3. La puissance par unité de volume est alors, dans Co et C respectivement,
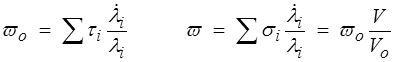
expression que nous retrouverons également plus loin, en remarquant que les vitesses de déformation (<) sont ici données par
où 
i =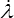 
i /λi est la dérivée par rapport au temps de la déformation logarithmique εi = ln λi. On remarque que le tenseur des taux de déformation D est la dérivée temporelle du tenseur des déformations de Hencky
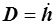
résultat précieux, on le verra, mais qui ne subsistera malheureusement pas dans le cas général. En particulier il permet ainsi d'identifier le tenseur Σ(o) conjugué des déformations logarithmiques au tenseur de contraintes de Kirchhoff. Plus généralement on peut aussi calculer simplement les contraintes Σ(m) conjuguées de Seth-Hill dans le cas m ≠ 0. On peut en effet écrire pour chaque composante
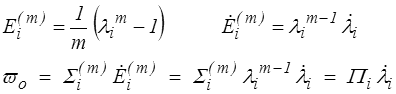
de sorte que
Traction simple
Dans ce contexte, et toujours en supposant le matériau isotrope, la traction simple s'obtient pour σ2 = σ3 = 0 et par symétrie λ2 = λ3
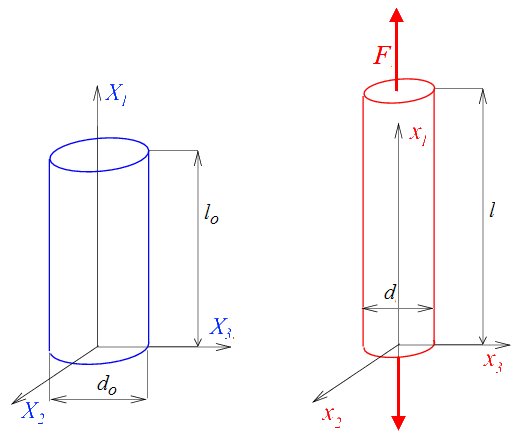
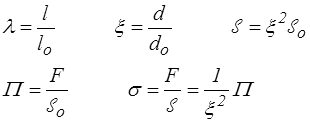
Dans un essai de traction (<) la contrainte Π est la contrainte nominale (engineering stress), tandis que σ est la contrainte vraie (true stress). La contrainte Π s'obtient directement à partir de l'essai, alors que le calcul de σ implique une correction de section . Ceci montre à nouveau le sens physique du premier tenseur de Piola-Kirchhoff.
La courbe de traction classique relie donc (pour les composantes 11) le tenseur PK1 au tenseur (U − 1) = E(1) tandis que la courbe rationnelle de traction (<) relie de même la contrainte de Cauchy à la composante 11 tenseur de Hencky.
D'un point de vue pratique, lorsque l'on saura écrire une loi de comportement, la condition σ2 = 0 permettra de déterminer la contraction ξ en fonction de l'allongement λ que l'on pourra ensuite relier à la contrainte de traction Π ou σ.
En MMC grandes transformations on fait souvent l'hypothèse d'incompressibilité. On aura alors
Comme dans le cas des fluides parfaits (<) ou visqueux (<) , la loi de comportement fera alors intervenir une pression hydrostatique arbitraire qui pourra alors être déterminée par la condition σ2 = 0.
La striction d'après Considere
Retenons de cet exemple que l'utilisation des déformations logarithmiques est une manière relativement saine d'aborder à peu de frais les grandes transformations. Les modèles que nous développerons plus loin suivront d'autres voies, mais en première approche on peut se souvenir que beaucoup de résultats obtenus en HPP pourront être étendus aux grandes transformations avec peu de risques si l'on utilise les déformations logarithmiques.
Un exemple classique est le modèle proposé par Considere (1885) pour le phénomène de striction.
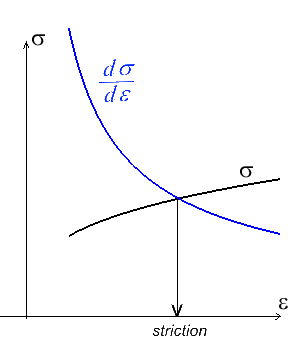Nous supposerons pour cela connue la courbe (rationnelle) de traction σ(ε) (σ contrainte de Cauchy, ε déformation logarithmique) et nous supposerons également le matériau incompressible. La force F appliquée sur l'éprouvette est alors donnée par
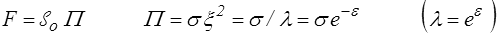
La striction, interprétée comme étant le maximum de la courbe de traction, s'obtient alors en écrivant
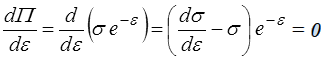
ce qui conduit à la condition de striction
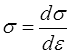
Pour les matériaux métalliques on modélise souvent la loi d'écrouissage σ(ε) par une loi puissance ( loi de Hollomon)
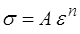
où n est appelé coefficient d'écrouissage (typiquement entre 0.1 et 0.5). La condition de Considere donnera donc
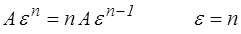
Remarquons que l'hypothèse d'incompressibilité est ici justifiée par l'incompressibilité plastique. Les déformations élastiques ne le sont pas (ν <1/2) mais elles peuvent à ce niveau de déformation être négligées.
Le passage par les grandes déformations était incontournable (la variation de section est en HPP négligée) mais on a pu le faire à moindre frais, presque en cachette.
Mouvements ρ-extensométriques
Nous terminons ce chapitre par un exemple, à première vue plus académique (encore que...), mais instructif. Nous nous limitons toujours aux matériaux incompressibles.
Un mouvement ρ-extensométrique est défini par
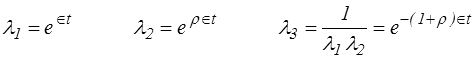
où ∈ est une vitesse de déformation constante et où ρ est un paramètre (−1 < ρ ≤ 1, attention à ne pas confondre avec la masse volumique, mais les risques de collision sont faibles). La traction simple, par exemple, correspond au cas ρ = −1/2.
Le tenseur des taux de déformation est alors
Il est constant, on parle d'un mouvement à histoire de déformation constante.
D'après l'incompressibilité le tenseur des contraintes (de Cauchy) fait intervenir une pression hydrostatique arbitraire. On pourra donc écrire
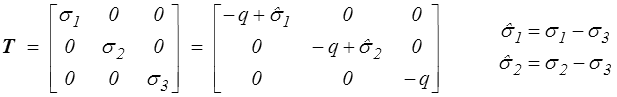
où 
1 et 2 seront évalués par la loi de comportement. Ces contraintes 1 et 2 correspondent par exemple aux contraintes qui se réalisent dans une situation de contraintes planes (<)
, comme plus haut en traction simple.
Appliquons cela au fluide visqueux newtonien (<)
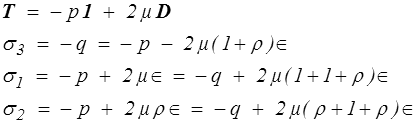
Soit finalement
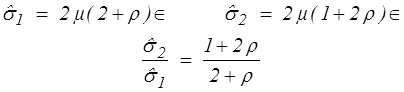
Ce résultat est en fait de portée beaucoup plus générale, et nous aurons l'occasion de le retrouver plus loin. On considérera notamment les cas particuliers suivants
- traction simple ρ = − 1/2 , 2 = 0
- extension équibiaxiale ρ = 1 , 2 = 1
- cisaillement ρ = − 1 , 2 = − 1