Thermoélasticité classique
Le modèle thermoélastique
L'élasticité linéaire (<) − modèle de base en mécanique des structures − ne prend pas en compte les couplages thermomécaniques. Leur introduction va nous conduire à la thermoélasticité. Au-delà de son intérêt fondamental, ce modèle sera important pour ses applications au calcul des contraintes thermiques, source majeure de sollicitations dans de nombreux problèmes.
Nous nous plaçons donc dans le cadre de l'hypothèse des petites perturbations (<) . L'équation de conservation de l'énergie (<) et l'inégalité de Clausius-Duhem (<) deviennent alors
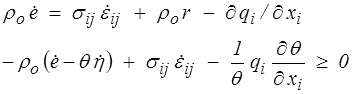
Nous supposons que l'énergie interne spécifique e dépend de la déformation y = εij et de l'entropie spécifique η
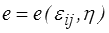
L'inégalité de Clausius-Duhem donne alors
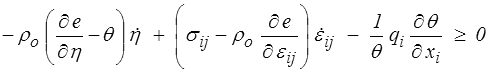
Nous supposons que la dissipation intrinsèque est nulle − C'est la thermoélasticité : la seule source de dissipation est la conduction thermique −. On aura donc les lois d'état
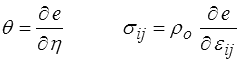
complétées, pour la conduction, par la loi de Fourier (<)
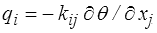
où le tenseur de conductivité kij peut dépendre de la température.
Nous utiliserons plutôt l'énergie libre ψ qui nous permettra d'écrire
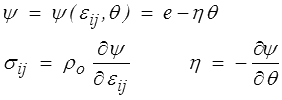
Thermoélasticité linéaire
Nous complétons l'hypothèse des petites perturbations en supposant que la configuration de référence correspond à une température de référence θo dont on s'écartera peu
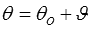
La thermoélasticité linéaire correspond au modèle linéarisé par rapport à εij et ϑ. On prendra donc ψ quadratique
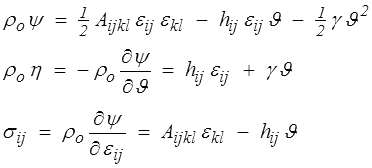
En toute rigueur ce n'est pas correct. Nous nous sommes limités dans l'énergie libre au terme quadratique, il faudrait en fait prendre également en compte les termes d'ordre inférieur
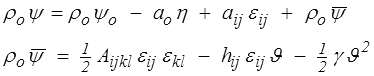
et écrire
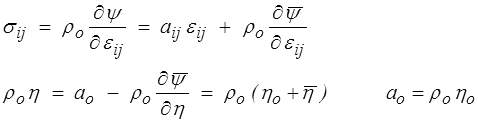
puisque dans la configuration de référence (εij = 0, θ = θo ) la contrainte est nulle, alors que l'entropie ηo comme l'énergie libre ψo ne sont pas nulles. Peu importe car seules nous intéressent les termes de perturbation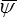 
et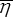 
. Nous nous autorisons donc l'abus d'écriture consistant à supprimer les barres et ne considérer que les termes quadratiques.
Le tenseur d'élasticité A est classique, tandis que le tenseur hij représente la contrainte induite par un échauffement à déformation bloquée (εij = 0). Pour se ramener à des notations plus courantes, nous inversons la loi thermoélastique en introduisant le tenseur de souplesse
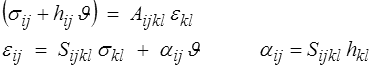
où αij représente la déformation induite, sous contrainte nulle, par une variation de température ; c'est la dilatation thermique. La loi élastique s'écrit donc plus traditionnellement
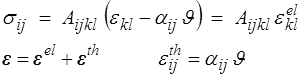
Quant au scalaire γ, il correspond à la chaleur spécifique (<)
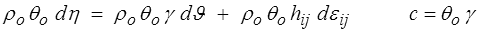
où c est la chaleur spécifique par unité de masse (à déformation constante).
Thermoélasticité linéaire isotrope
Comme en élasticité le modèle thermoélastique classique s'obtiendra en rajoutant l'hypothèse d'isotropie. La partie élastique de la déformation est alors donnée par la loi de Hooke et la dilatation thermique est isotrope
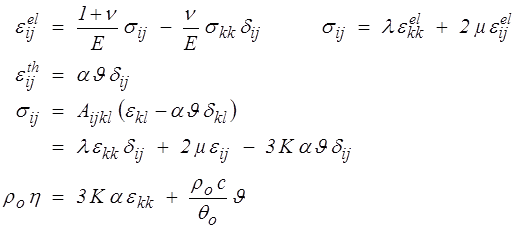
De même la loi de Fourier devient
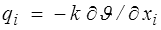
Le modèle thermoélastique classique fait donc intervenir 5 constantes
- 2 constantes élastiques (isothermes) E, ν ou λ, μ ou K, G (<) ,
- le coefficient de dilatation thermique (linéaire) α,
- la chaleur spécifique (à déformation constante) c,
- le coefficient de conduction thermique k.
Puisque le couplage thermomécanique ne porte que sur les parties sphériques, il pourra être commode d'écrire la loi de Hooke sous sa forme découplée, déviateur partie sphérique (<) ,
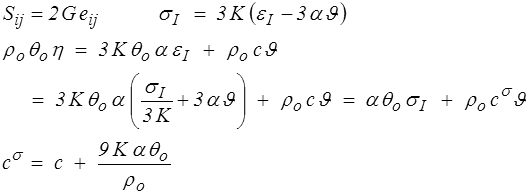
relation entre les chaleurs spécifiques à contraintes constantes c σ et à déformation constante c (c'est l'analogue de la relation classique entre C p et C v en thermodynamique des fluides).
On peut aussi écrire de manière symétrique
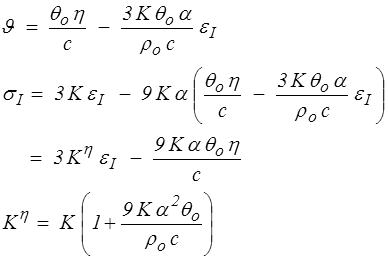
relation entre les modules de compressibilité isotherme K et isentropique K η (les modules de cisaillement sont égaux, G η = G).
Problèmes de thermoélasticité
En thermoélasticité, comme en élasticité (<) , nous devrons formuler puis résoudre un problème aux limites. Nous devons pour cela compléter les équations du mouvement par l'équation de conservation de l'énergie (<)
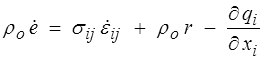
où l'énergie interne e est fonction de εij et de l'entropie spécifique. Les lois thermoélastiques que nous venons d'écrire donnent alors en HPP (θ ≈ θo )
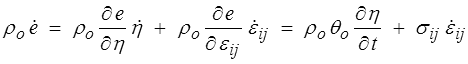
Les équations du problème sont donc
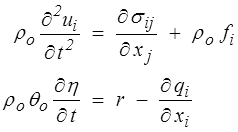
qui, complétées par les lois de comportement, conditions initiales et conditions aux limites, permettront de calculer les champs de déplacement ui(x,t) et de température ϑ(x,t).
Les conditions initiales doivent imposer les positions, vitesses (<) et température à l'instant initial
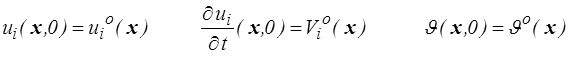
Les conditions aux limites mécaniques (<) doivent être complétées de conditions thermiques, imposant par exemple la température sur une partie Sθ de la frontière et le flux de chaleur sur la partie complémentaire Sq
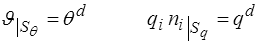
Les lois de comportement thermoélastiques donnent les contraintes et l'entropie tandis que le flux de chaleur obéit à la loi de Fourier. On obtient ainsi en thermoélasticité classique
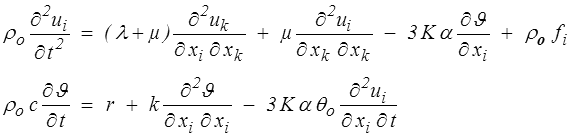
Thermoélasticité découplée
Le dernier terme de la seconde équation disparait dans le cas statique ∂ui /∂t = 0 et il est, même dans le cas instationnaire, souvent négligeable. On retrouve alors l'équation de la chaleur classique qui permettra de déterminer, indépendamment des sollicitations mécaniques, le champ de température. Il suffit alors de reporter dans la première équation (et aussi dans les conditions aux limites) pour obtenir un problème élastique classique dans lequel le champ de température intervient comme une sollicitation extérieure.
C'est la thermoélasticité découplée. On se retrouve d'ailleurs dans la même situation lorsque l'on part d'un champ de température donné a priori (déterminé par exemple expérimentalement).
C'est le modèle de base pour l'étude des contraintes thermiques, dominantes dans de nombreux domaines applicatifs.