Équations constitutives
Milieux matériellement simples
Dans la culture « grandes transformations » on parle souvent d'équations constitutives en lieu et place de lois de comportement. Cette coquetterie terminologique me permet surtout d'insister à nouveau sur le fait que nos modèles ne sont pas la réalité physique mais une construction intellectuelle. Nous ne sommes pas dans le monde physique mais dans le monde platonique des idées, cher à Roger Penrose (The Road to Reality, Jonathan Cape, 2004, dont je ne saurais trop recommander la lecture, au moins des premiers chapitres). La loi de comportement est, en ce sens, ce qui « constitue » le modèle, son essence même. Quant à son intérêt ou son utilisation pour décrire tel ou tel matériau ou résoudre un problème pratique, c'est une question importante mais distincte.
La loi de comportement, en grandes déformations comme en petites, reliera contrainte et déformation. Nous avons vu qu'il existait bien des manières de décrire l'une et l'autre, lesquelles choisir ? La réponse à cette question se décantera progressivement et nous verrons qu'elle dépend largement du type de comportement envisagé. Nous nous limiterons pour l'instant à une forme générique reliant le premier tenseur de Piola-Kirchhoff au tenseur gradient. Nous écrirons donc de manière générale, en généralisant l'écriture HPP (<) ,
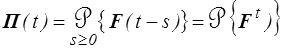
La valeur actuelle du tenseur PK1 dépend de l'histoire passée du gradient de déformation (fonctionnelle héréditaire causale, mémoire du matériau). La première écriture nous est déjà connue, la seconde un peu plus abstraite note F t l'histoire passée de F, c'est à dire la fonction
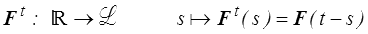
Attention à ne pas confondre avec la déformation relative Ft (<) : on rencontrera plus loin Ftt, histoire de la déformation relative.
Le choix de F pour représenter la déformation est assurément trop large puisque le tenseur gradient fait intervenir (outre la déformation) la rotation qui ne doit pas intervenir dans la loi de comportement. Il faudra affiner, mais nous sommes au moins certains de ne rien rater. Quant au choix de Π pour représenter la contrainte il ne nous engage en rien puisque tous les autres pourront se calculer à partir de Π et de F(t) (<)
. Il est sympathique car Π et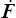 
sont des variables duales (<)
mais nous aurions aussi bien pu choisir T ou S ou etc...
Ce cadre définit ce que l'on appelle les milieux matériellement simples, l'essentiel étant que seul y intervient le premier gradient du mouvement.
Remarquons aussi que, contrairement à ce qui se passait en HPP, l'écriture symétrique donnant la déformation en fonction de la contrainte n'est pas possible : le tenseur gradient inclut la rotation qui ne peut pas être déterminée par les contraintes.
Les deux mémoires
En introduisant la déformation relative (<) nous pouvons aussi écrire
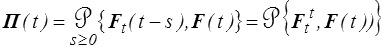
introduisant l'histoire de déformation relative
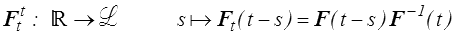
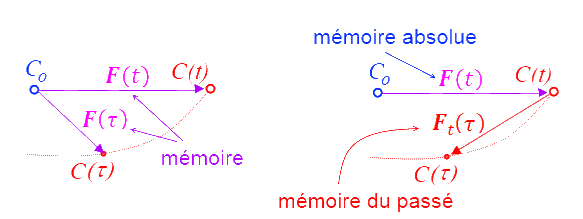
Ce changement de variable, bien innocent pourrait-on croire, est en fait porteur de sens car il distingue 2 mémoires très différentes. Ceci est schématisé sur le dessin ci-dessus.
- Par la déformation F(t) le matériau conserve la mémoire de sa configuration de référence − souvent choisie comme étant une configuration naturelle, libre de contraintes. On parlera de « mémoire absolue ».
- Par la déformation relative F(t − s) le matériau se souvient de ce qui lui est arrivé; on parlera de « mémoire du passé », et on lui adjoindra souvent une hypothèse (pas toujours justifiée) de mémoire évanescente. Le matériau se souvient de tout ce qui lui est arrivé, mais surtout de ce qui s'est passé récemment, il oublie progressivement ce qui lui est arrivé voici longtemps.
En osant une métaphore génétique, la mémoire absolue correspond à l'inné (le matériau a dans ses gènes sa configuration de référence), la mémoire du passé correspond à l'acquis (il a été formé par ce qu'il a subi). Le poids relatif de ces deux mémoires jouera dans la classification des matériaux un rôle essentiel.
Un premier survol
Tout comme en HPP (<) , cette forme fonctionnelle, pour essentielle et générale qu'elle soit, est rarement utilisée en tant que telle, et nous allons maintenant passer en revue différentes classes de modèles couramment utilisés. Cette présentation restera, comme l'ensemble de cette page, largement formelle et symbolique. Elle vise simplement un panorama d'ensemble qu'il sera utile de garder présent à l'esprit avant d'aborder l'étude plus systématique de ces modèles.
Le cas le plus simple est le cas des matériaux élastiques
Π(t) = π ( F(t) )
La contrainte est fonction de la déformation, ce qui correspond à la mémoire absolue sans mémoire du passé. Les lois de Hooke généralisées (<) en sont un cas particulier.
Pour un matériau visqueux, on rajoute les vitesses de déformation
Π(t) = π ( F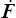(t),(t) )
comme pour le modèle de Kelvin-Voigt (<) . Ceci correspond à une forme élémentaire de la mémoire du passé. On montre en effet
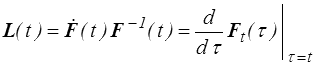
On peut rajouter les dérivées d'ordres supérieurs, par exemple au second ordre
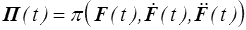
Ces modèles ont été utilisés notamment en mécanique des fluides, et nous les évoquerons plus loin mais c'est, à mon avis, de l'histoire ancienne. En particulier ils réagiront à une discontinuité de contrainte (<) par une discontinuité de la dérivée seconde de la déformation et non par une discontinuité de la vitesse de déformation (viscosité) ou de la déformation (élasticité instantanée).
Plus intéressants sont les matériaux de type taux
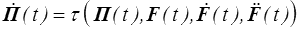
qui généraliseront les lois différentielles, comme par exemple ce que l'on a obtenu en HPP pour le modèle de Maxwell (<) ou de Poynting/Zener (<) .
Comme en HPP toutefois, nous privilégierons les modèles à variables internes (<) pour lesquels nous écrirons simplement
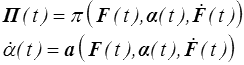
Nous pouvons reprendre mot pour mot la comparaison faite alors (<) avec la description fonctionnelle générale.
Ceci reste encore une coquille vide qu'il conviendra de remplir, mais il est utile de conserver en mémoire cette classification.
Un modèle variationnel
En élastostatique le théorème de l'énergie potentielle permet d'obtenir la solution par minimisation de l'énergie potentielle (<) . Peut-on extrapoler aux grandes déformations ?
Soit donc un solide occupant avant déformation un domaine Do choisi comme configuration de référence Co. Après déformation ce solide occupe une configuration C1 définie par la fonction x(X). Le mouvement est imposé sur une partie Su de la frontière de Do, tandis que des efforts surfaciques T d (dont la nature précise reste à clarifier) sont donnés sur la partie complémentaire Sf
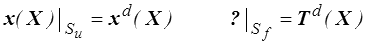
Par analogie avec le théorème HPP (<) nous cherchons la solution x par la propriété variationnelle
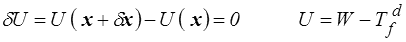
où le CCA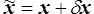 
vérifie la condition aux limites sur Su ( δx = 0 sur Su ).
Pour le travail des efforts donnés nous écrirons naturellement
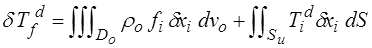
Pour W nous postulons une densité d'énergie de déformation w fonction de F
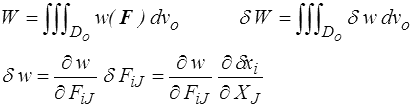
Remarquons au passage que nous ne sommes ici même pas posé de question quant au choix de la description (eulérienne ou lagrangienne?). Dans un problème réel on connait le domaine initial Do alors que le domaine déformé D est une des inconnues du problème. Le choix lagrangien s'impose naturellement.
La variation δ W s'obtient par application du théorème de la divergence (<) sur Do
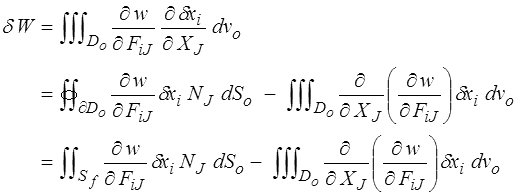
La condition variationnelle δ U = 0 s'écrira donc finalement
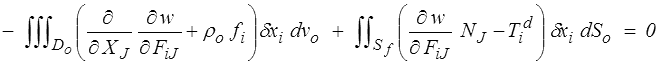
pour toute variation δx. Il vient donc
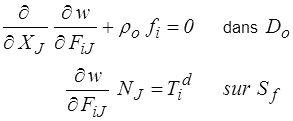
On retrouve dans Do les équations d'équilibre exprimées en fonction du premier tenseur de Piola-Kirchhoff (<) . Avec cette interprétation les relations précédentes deviennent
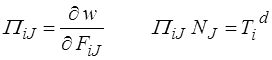
Nous obtenons ainsi une loi de comportement et des conditions aux limites portant sur les efforts surfaciques et plus précisément sur le vecteur to, force par unité de surface dans Co (<) . Ces conditions aux limites sont dites de « charge morte ». D'un point de vue mathématique comme d'un point de vue physique, ce sont les conditions aux limites les plus naturelles. Le tenseur PK1 s'avère un fois de plus porteur de sens physique.
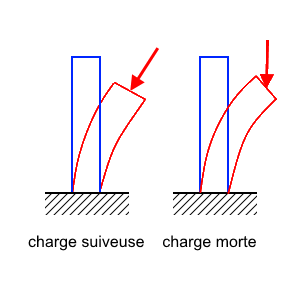C'est là une difficulté majeure en grandes transformations : pour imposer des efforts surfaciques, il importe de savoir comment ils dépendent de la configuration déformée qui est une inconnue du problème. Pour un problème de flambement par exemple on peut distinguer en fonction de la technologie de l'application de la force de compression appliquée, des conditions de charge morte ou de charge suiveuse, et il s'agit de deux problèmes très différents. Les conditions de charge morte que nous avons trouvées ici sont les plus simples à mettre en oeuvre.
Liaisons internes
Lorsqu'une restriction cinématique est imposée aux mouvements possibles − par exemple l'incompressibilité − alors il convient de modifier la loi de comportement générale en rajoutant à la contrainte une partie arbitraire ne travaillant pas dans tout mouvement compatible avec la liaison
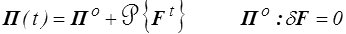
Nous reviendrons plus loin sur l'origine et la signification de cette partie arbitraire, mais nous l'accepterons pour l'instant telle quelle. Remarquons toutefois que dans le cadre de l'approche variationnelle présentée ci-dessus cette contrainte indéterminée correspond au multiplicateur de Lagrange associé à la liaison imposée.
L'application la plus importante est l'incompressibilité − hypothèse très courante en grandes transformations, nous y reviendrons. Elle se traduit par
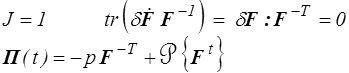
ou, si l'on préfère le tenseur des contraintes de Cauchy (<) ,
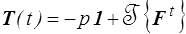
et on retrouve la pression hydrostatique arbitraire classique en mécanique des fluides (<).
Un autre exemple correspond au cas d'un matériau inextensible dans une direction matérielle M, soit (<)
Il est alors commode de travailler sur le tenseur PK2 S dual de C ou E (<) , plutôt que sur Π,
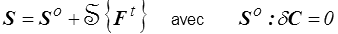
On aura donc
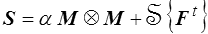
ou, en revenant au tenseur de Kirchhoff,
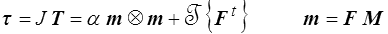
La partie indéterminée du tenseur des contraintes correspond à une tension uniaxiale dans la direction d'inextensibilité.
Indifférence matérielle
Le tenseur gradient de déformation F combine déformation et rotation. La loi de comportement, relation entre contrainte et déformation, ne doit pas faire intervenir la rotation, qu'il faut donc éliminer. C'est une question importante et nous y reviendrons souvent dans la suite. Il importe néanmoins d'en poser dès à présent les bases.
L'idée la plus naturelle est d'affirmer que la superposition d'un mouvement de corps rigide ne change pas l'état de contrainte. En termes simples le résultat d'un essai mécanique (traction par exemple) sera le même, que la machine et le matériau d'essai soient immobiles ou en mouvement.
La correspondance entre mouvement de solide rigide et changement de référentiel (<) permet la formulation suivante, plus traditionnelle,
Principe d'indifférence matérielle.
La loi de comportement est invariante par changement de référentiel
x' = Q(t) x + c(t)
Nous en restons là pour l'instant et nous verrons plus loin la mise en ouvre de ce « principe ».
On remarque que cette invariance imposée est beaucoup plus forte que l'invariance galiléenne qui est au cœur de la mécanique newtonienne (invariance des lois de la physique par changement de repère galiléen − c'est-à-dire en translation uniforme l'un par rapport à l'autre). La loi de comportement, conséquence macroscopique des interactions atomiques, moléculaires ou autres, n'a donc aucune raison de vérifier cette invariance plus forte. C'est davantage une hypothèse généralement acceptée et pertinente qu'un « principe » universel. D'ailleurs il semble que la théorie cinétique des gaz (qui au premier ordre conduit au fluide visqueux newtonien) puisse donner au second ordre une loi de comportement violant ce principe.
Symétries matérielles
Un matériau sera isotrope s'il présente les mêmes propriétés dans toutes les directions, c'est à dire si sa loi de comportement est invariante par rotation de la configuration de référence. Plus généralement les symétries matérielles correspondent à l'invariance de la loi de comportement sous certaines transformations de la configuration de référence
et on définira
Définition.
Le groupe d'isotropie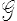 
est l'ensemble des transformations P laissant inchangée la loi de comportement.
Ce groupe dépend évidemment de la configuration de référence choisie. Les symétries matérielles ne peuvent être définies que par rapport à une configuration de référence Co particulière et judicieusement choisie − une configuration naturelle libre de contrainte par exemple. C'est en tout cas une configuration physique et significative pour le matériau, et non plus, comme jusqu'à présent, un repérage plus ou moins arbitraire des particules.
Comme pour l'indifférence matérielle c'est une notion essentielle sur laquelle nous reviendrons largement dans la suite.
Il importe par contre de bien comprendre la différence entre indifférence matérielle et symétrie matérielle / isotropie
Il s'agit dans les deux cas d'invariance de la loi de comportement, mais concernant des transformations
- dans Co pour les symétries matérielles,
- dans C(t) pour l'indifférence matérielle.
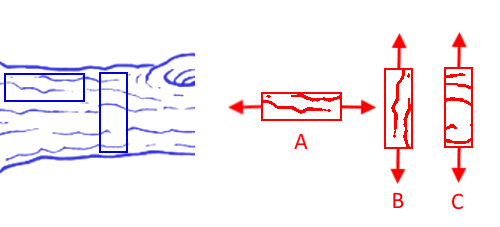
Dans le schéma ci-dessus :
- L'indifférence matérielle affirme que les essais A et B donnent le même résultat.
- L'isotropie compare le résultat des essais A et C.