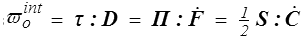Le premier principe
Conservation de l'énergie
Le premier principe de la thermodynamique exprime un bilan d'énergie : la variation de l'énergie d'un système est la somme des apports d'énergie − mécanique, thermique ou autre − venant de l'extérieur. La thermodynamique classique considère des systèmes homogènes où les grandeurs thermodynamiques (pression, température, contraintes,...) sont uniformes. Il nous faut maintenant l'étendre à un système continu hétérogène pour lequel ces grandeurs thermodynamiques deviennent des champs variables d'un point à l'autre.
Nous considérons comme système thermodynamique un domaine matériel, c'est donc pour le thermodynamicien un système fermé (il échange travail et chaleur avec l'extérieur, mais pas de matière). Le premier principe s'écrit alors (<)
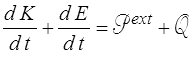
Par rapport à la thermodynamique classique (<) et outre quelques changements de notations (puissance plutôt qu'énergie ; l'énergie interne est notée E) nous avons surtout rajouté l'énergie cinétique, négligée car négligeable pour les systèmes homogènes considérés en thermodynamique classique.
Le modèle proto-thermodynamique (c'est-à-dire pour nous la MMC) nous a donné l'expression de l'énergie cinétique et de la puissance des efforts extérieurs.
La thermodynamique introduit deux nouvelles quantités
- E est l'énergie interne,
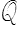représente la chaleur apportée au système par unité de temps.
Le théorème de l'énergie cinétique (<) nous a même permis de transformer cette écriture en
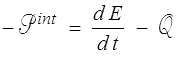
Hypothèse de l'état local
L'énergie interne est une fonction extensive et additive. On l'obtiendra donc en faisant la somme des énergies internes de tous ses éléments de volume. On écrira simplement
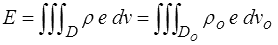
où e est l'énergie interne spécifique, c'est-à-dire la densité massique d'énergie interne (plutôt que volumique, car celle-ci dépendrait de la configuration choisie).
En d'autres termes on suppose que chaque élément de volume se comporte comme un système homogène (ou presque, à condition d'être suffisamment petit) dont on peut suivre l'état thermodynamique défini par des grandeurs thermodynamiques locales. On parle souvent d'« hypothèse de l'état local ».
D'un point de vue pratique et expérimental, on se heurtera alors à la difficulté déjà rencontrée pour écrire une loi de comportement (<) . Il faudra reconstituer cet état thermodynamique homogène sur une éprouvette, par exemple notre barreau en traction. Il n'était déjà pas facile de réaliser des essais mécaniques homogènes (<) , et si l'on impose en plus l'homogénéité thermique, cela devient presque mission impossible. Les techniques de calorimétrie restent néanmoins tout à fait efficaces et leur utilisation en mécanique des matériaux est désormais courante. Les progrès de la modélisation et du calcul numérique permettent par ailleurs, comme en mécanique, l'utilisation d'essais non homogènes (notamment par thermographie infrarouge).
Les échanges de chaleur
Restent à caractériser les échanges de chaleur. L'analogue du postulat de Cauchy nous conduit à poser pour la quantité de chaleur apportée au système
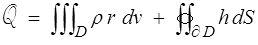
avec
- un apport volumique ρ r. Ce terme sera souvent nul, mais il pourra par exemple correspondre à la chaleur engendrée par des réactions nucléaires (c'est semble-t-il le phénomène qui pilote la thermique du globe terrestre). Ce sera aussi dans un modèle bidimensionnel de plaque un apport externe de chaleur (chalumeau, impact laser,...). Il importe par contre de bien souligner ce qu'il n'est pas : l'apport de chaleur résultant de la dissipation ou du mouvement (convection) ; ces échanges-là interviendront naturellement dans notre modèle. En tout état de cause cet apport de chaleur est, comme les forces volumiques, une donnée du problème, et en fait il sera le plus souvent pris nul.
- un apport surfacique par conduction. h représente le flux de chaleur au travers de la surface dS.
La thermique invoque traditionnellement 3 modes de transfert de chaleur : deux d'entre eux (la conduction et la convection) sont naturellement inclus dans notre modèle. Pour le troisième, le rayonnement, c'est moins clair. Peut-être peut-il aussi contribuer au terme d'apport volumique ?
L'équation de conservation de l'énergie
Nous sommes maintenant en mesure d'écrire en MMC, et à partir de l'expression de la puissance des efforts intérieurs, le premier principe pour un domaine matériel
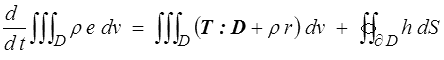
Rappelons que dans ce cours nous notons T le tenseur des contraintes de Cauchy que nous notions précédemment σ en HPP (<) .
Cette formulation, comme la loi fondamentale (<) , correspond à la structure générale d'une loi de conservation : la variation de l'énergie interne résulte des apports volumiques et surfaciques. La démarche générale pour l'exploiter a déjà été mise en place pour la loi fondamentale, il suffit de paraphraser ce que nous avions fait alors.
On commence par postuler que le flux de chaleur h ne dépend de la surface ∂D que par sa normale extérieure n. On montre ensuite (petit disque, puis petit tétraèdre), qu'il en dépend linéairement
h = − q . n
où q est le vecteur flux de chaleur. Le théorème de la divergence (<) et le théorème de Reynolds conduisent alors à
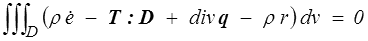
d'où l'on tire finalement la forme locale du premier principe de la thermodynamique
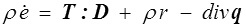
Un premier bilan
Nous pouvons maintenant, comme nous l'avons fait en mécanique des milieux continus (<) , dresser un bilan des inconnues et des équations disponibles pour formuler et résoudre un problème de thermomécanique des milieux continus.
Les inconnues fondamentales sont
- le mouvement du système x(X,t) ou V(x,t),
- le champ de température θ(X,t) ou θ(x,t),
et nous disposons des deux lois de conservation qui traduisent la loi fondamentale et le premier principe
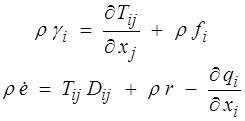
Pour fermer ce système d'équations nous aurons donc besoin de lois de comportement permettant de déterminer en fonction du mouvement et de la température :
- le tenseur des contraintes : c'est la loi de comportement mécanique sur laquelle nous avons déjà beaucoup travaillé,
- l'énergie interne spécifique : c'est en langage thermodynamique une loi d'état du système local pour laquelle il sera commode d'utiliser un potentiel thermodynamique (<)
- le vecteur flux de chaleur q : c'est la loi de la conduction (loi de Fourier) que nous verrons très prochainement apparaître,
- la masse volumique ρ que, par un réflexe de mécanicien du solide j'avais presque oubliée, tant elle est pour moi inclue dans le mouvement puisque (<) ρ J = ρo. Un mécanicien des fluides rajoutera ρ(x,t) à la liste des variables fondamentales avec en vis-à-vis, l'équation de continuité (<) . C'est uniquement une question de présentation.
Formulation lagrangienne
Je me suis limité à une formulation eulérienne : le premier principe s'écrit naturellement dans l'espace physique eulérien. On peut bien évidemment, comme nous l'avons fait pour la loi fondamentale (<) , en donner une version lagrangienne.
Nous avons déjà discuté la puissance des efforts intérieurs (<) . Il faudra par contre introduire un flux de chaleur lagrangien pour écrire l'apport de chaleur sous la forme
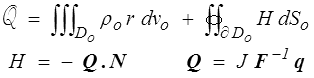
puisque, en utilisant la formule de Nanson (<) ,
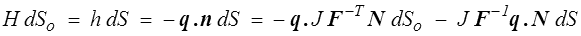
L'équation de l'énergie s'obtiendra alors directement sous la forme
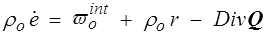
où Div Q = ∂QI / ∂XI est la divergence lagrangienne du flux de chaleur lagrangien Q et où ϖoint est la puissance des efforts intérieurs par unité de volume dans Co (<)
