Milieux à double température
Les deux températures
L'inégalité de Clausius-Duhem, traduction usuelle du second principe de la thermodynamique, n'est pas la seule possible, et diverses alternatives ont été développées. Nous présenterons, à titre d'exemple, l'une d'entre elles, le modèle à deux températures. Nous partons toujours du second principe tel qu'il a été écrit en MMC (<) mais nous prenons maintenant pour l'apport extérieur d'entropie
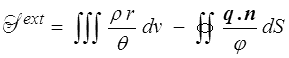
en distinguant la « température conductive » φ de la température volumique θ. Je ne discuterai pas les arguments − plus ou moins convaincants − mis en avant pour justifier cette écriture. Ma motivation essentielle en présentant cet exemple est plutôt de tester la robustesse du modèle usuel en analysant les conséquences d'une altération des hypothèses. Cet exemple nous permettra par ailleurs d'éclairer quelques aspects méthodologiques intéressants, notamment l'utilisation, comme alternative à la TPI, de la thermodynamique rationnelle (<) .
Écriture du second principe
Pour expliciter les conséquences de cette hypothèse, nous nous limiterons au modèle thermique. La prise en compte du couplage thermomécanique, par exemple pour un modèle thermoélastique, ne pose pas de problèmes spécifiques mais compliquerait inutilement les choses.
Le premier principe s'écrit alors
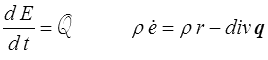
tandis que le second principe est
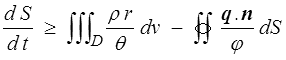
ou sous forme locale
On combine ces deux équations pour éliminer l'apport extérieur de chaleur
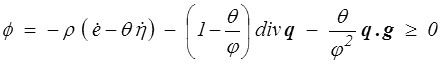
ou, en introduisant l'énergie libre ψ = e − θη,
Cette inégalité fondamentale remplace maintenant l'inégalité de Clausius-Duhem (<) .
La température volumique θ doit alors au même titre que ψ, η et q être donnée par l'ensemble des lois de comportement.
Le modèle de base
Nous supposerons donc que ψ, η, θ et q sont fonctions de φ et g = grad φ. Conformément à la règle d'équiprésence (<) , nous partons donc de
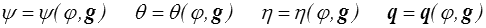
Il sera toutefois plus commode d'utiliser comme variable de base pour l'énergie libre la température volumique θ plutôt que la température conductive φ. Nous supposons donc que la fonction θ(φ,g) est inversible pour donner φ = φ(θ,g) et nous considérons plutôt ψ comme fonction de θ et g
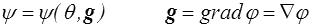
Pour reporter dans l'inégalité fondamentale nous devons calculer
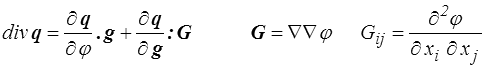
et nous définissons le tenseur de conductivité
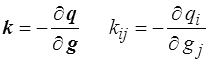
L'inégalité fondamentale devient alors
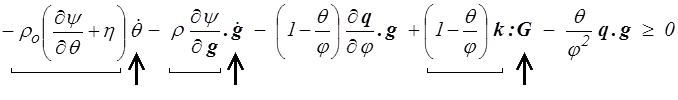
Conformément à la démarche générale de la thermodynamique rationnelle (<)
on fixe θ et g. D'après les lois de comportement, tous les termes soulignés sont alors imposés tandis que les dérivées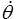 
, 
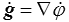et G = ∇∇φ peuvent être choisies arbitrairement ; on en tire donc
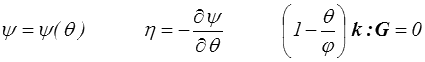
Les deux premières relations ne nous étonnent guère, on remarque simplement que c'est bien θ et non φ qui joue le rôle de la température thermodynamique.
La troisième relation doit être vérifiée pour tout G symétrique. Ceci implique l'une ou l'autre des deux conditions suivantes.
- les deux températures coïncident, et on retrouve le modèle classique basé sur l'inégalité de Clausius-Duhem.
- le tenseur de conduction k est antisymétrique, situation très étrange assurément, mais non exclue par la thermodynamique qui impose simplement à sa partie symétrique d'être semi-définie positive. Je n'insiste pas, mais ceci montre que la thermodynamique à elle seule n'impose finalement que peu de choses.
Second gradient
Ainsi, et si l'on exclut l'éventualité exotique d'un tenseur de conductivité antisymétrique, le choix initial des variables (φ,g) nous impose l'égalité des deux températures et nous ramène au modèle classique. Pour aller plus loin nous rajoutons aux variables d'état le second gradient de température G = ∇∇φ.
Nous supposons donc désormais que ψ, η, q et θ peuvent dépendre de φ, g = ∇φ et G = ∇∇φ, et moyennant pour l'énergie libre le changement de variable (φ,g,G) → (θ,g,G) on obtient maintenant
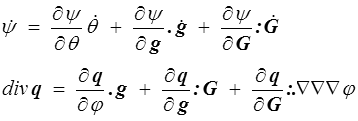
On remarquera que le tout dernier terme fait intervenir des tenseurs du 3me ordre (dérivée d'un vecteur par rapport à un tenseur, troisième gradient), d'où ma notation à 3 points pour leur produit scalaire. En toute rigueur et pour suivre les consignes données (<) , je devrais passer en composantes. Je me permettrai donc dans l'ensemble de ce paragraphe quelques libertés. De toute façon, l'essentiel n'est pas là.
L'inégalité fondamentale s'écrit finalement
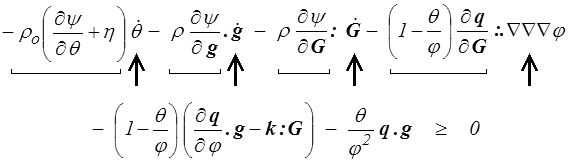
On fixe φ, g, G et donc aussi, d'après les lois de comportement, θ et les termes soulignés, tandis que les dérivées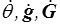 
et ∇∇∇φ peuvent être choisies arbitrairement. On en déduit que tous les termes soulignés de la première ligne doivent s'annuler − ou presque. On en déduit, comme plus haut,
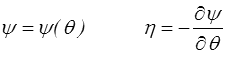
et, en laissant de côté la solution triviale θ = φ,
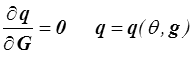
ou presque ? Pourquoi ?
car toujours en excluant le cas θ = φ l'inégalité impose simplement que la quantité
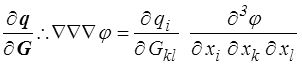
soit nulle pour tout tenseur du troisième ordre entièrement symétrique. Le tenseur du troisième ordre ∂q/∂G peut être non nul à condition de vérifier des conditions d'antisymétrie que je n'exploite pas davantage.
Il ne reste alors plus que la seconde ligne
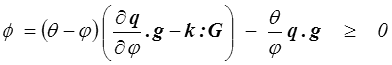
La dissipation ϕ, fonction de φ, g et G, doit être identiquement positive ou nulle.
Analyse de la dissipation
Pour analyser les conséquences de cette inégalité nous utilisons le résultat général donné plus haut (<)
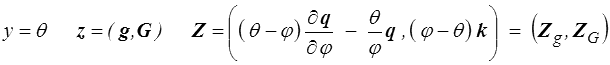
La condition Zo = 0 donne en supposant k non nul
A l'équilibre les deux températures sont égales et le flux de chaleur est nul.
Il faut ensuite imposer à l'opérateur χo d'être semi-défini positif. Nous posons
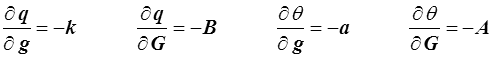
On obtient alors pour les blocs constituant χ
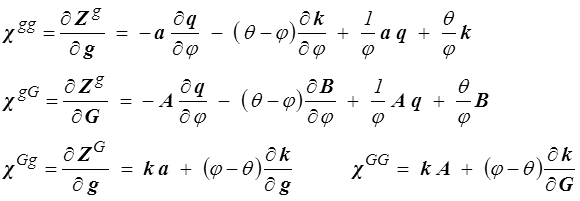
Ce résultat est assez lourd, un peu formel car faisant intervenir des tenseurs du troisième et du quatrième ordre, ( à nouveau les notations tensorielles intrinsèques posent problème, il faudrait revenir aux notations indicielles, et en toute honnêteté vérifier ; je garantis l'essentiel mais pour le reste...)
A l'équilibre par contre cela se simplifie pour donner finalement
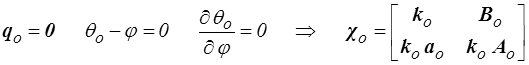
La condition χo ≥ 0 s'écrit donc
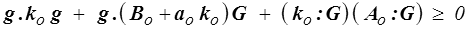
pour tout vecteur g et tout tenseur symétrique G.
En prenant G = 0 on trouve encore un tenseur de conductivité semi-positif, ceci ne concernant rappelons-le que sa partie symétrique, la thermodynamique n'impose aucune restriction à sa partie antisymétrique.
De même, en prenant g = 0, il vient
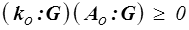
pour tout tenseur G symétrique. On montre simplement que ceci impose au tenseur symétrique Ao d'être proportionnel à la partie symétrique de ko
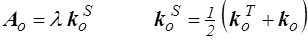
Un modèle linéaire
Cela ne suffit pas : il faudrait aussi écrire une condition sur les termes croisés. Cette condition sera vérifiée si les coefficients correspondant à ces termes croisés, a et B, ne sont pas trop grands par rapport aux coefficients de la diagonale. Pour simplifier je les supposerai désormais nuls a = B = 0 et je me limiterai à un modèle linéaire. On aura donc
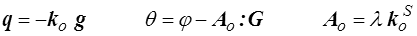
où λ est un coefficient positif. Ce modèle généralisé de conduction fait intervenir à côté du tenseur de conduction ko un coefficient supplémentaire λ qui contrôle l'écart entre les deux températures, le modèle classique correspondant à la limite λ → 0.
Pour un milieu isotrope les termes de couplage sont nuls (c'est dans ce cas un théorème) et les deux tenseurs ko et Ao sont sphériques
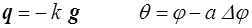
Ceci conduira notamment à une équation de la chaleur modifiée
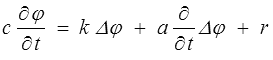
Retour à la TPI
Nous avons développé ce modèle dans le cadre de la thermodynamique rationnelle et c'est effectivement dans ce cadre qu'il l'a été. Mais était-ce indispensable ? Que donneraient dans ce contexte la TPI et les relations d'Onsager ? Pour explorer cette piste, nous partons de la dissipation (<) et en supposant ψ fonction de θ il vient
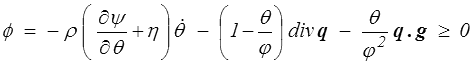
Aux deux termes usuels se rajoute un nouveau terme directement lié à l'écart entre les deux températures, le flux thermodynamique correspondant étant la divergence du vecteur flux de chaleur. Comme toujours (<) nous annulons le premier terme (dissipation entropique) et il reste
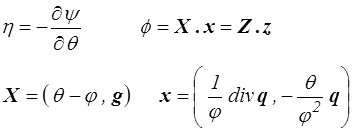
Les relations d'Onsager s'écrivent alors
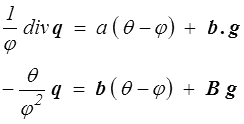
On peut aussi, pour se rapprocher du modèle issu de la thermodynamique rationnelle, choisir comme variables dépendantes θ − φ et q. Il faut alors utiliser les relations de Casimir-Onsager (<)
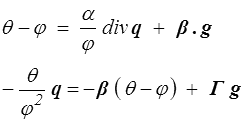
Mais cela ne nous donne rien d'exploitable dans le cas général. Si par contre les termes croisés sont nuls (β = b = 0) alors il vient
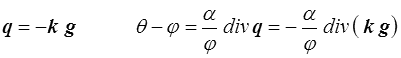
soit, si le tenseur de conduction k est constant,
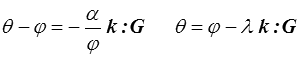
soit à peu prés le modèle obtenu dans le cas découplé par la thermodynamique rationnelle.
Quelques éléments de réflexion
On n'attachera pas trop d'importance au modèle particulier que nous venons de construire. Ce n'est qu'un exemple de ce que l'on peut faire, et il existe d'autres manières de remettre en cause l'inégalité de Clausius-Duhem qui apparaît ici comme un modèle particulier (modèle de premier gradient en thermodynamique rationnelle, absence de dissipation liée à l'écart de température θ − φ en TPI).
L'inégalité de Clausius-Duhem, comme tout ce que nous faisons dans ce cours et plus généralement en mécanique, n'est pas LA physique mais une modélisation utile et efficace certes, mais qu'il peut être tout à fait légitime de contester. Il en va de même de la TPI, dont nous avons ici perçu les limites ; la thermodynamique rationnelle me semble ici être une voie plus sûre.
Une dernière remarque pour conclure : on a vu que l'on retrouvait θ = φ et Clausius-Duhem pour le modèle au premier gradient. Réciproquement, si l'on a des raisons de croire que le second gradient de température joue un rôle, alors ces modèles généralisés deviennent beaucoup plus pertinents. C'est, transposée à la thermodynamique, toute la problématique des milieux continus généralisés, domaine qui prend actuellement une grande importance.