Thermodynamique des Fluides
Le fluide thermodynamique
La présentation traditionnelle de la thermodynamique classique s'appuie, de manière privilégiée, sur les systèmes fluides (gaz parfaits, fluides de van der Waals,...). C'est effectivement un modèle très important, tant par ses applications aux machines que par le rôle historique essentiel qu'il a joué dans le développement de la discipline. C'est aussi un modèle très simple. On part du premier principe (<)
d U = − p dV + đ Q
et le second principe conduit à introduire l'entropie et la température absolue, puis les quatre potentiels thermodynamiques : énergie interne, enthalpie, énergie libre et enthalpie libre, fonctions des variables choisies : p ou V pour la mécanique, S ou T pour la thermique (<) .
En thermodynamique des milieux continus, l'hypothèse de l'état local (<) nous permet de réutiliser tous ces résultats pour l'élément de volume en considérant pour les grandeurs extensives (U, V, S,...) les densités massiques. L'énergie interne spécifique sera donc fonction
- de l'entropie spécifique,
- du volume spécifique (volume par unité de masse) auquel, par tradition, nous substituons la masse par unité de volume, ρ = dm / dV.
Calcul de la dissipation
L'énergie interne spécifique e sera donc fonction de ρ et η, et nous pouvons reporter dans l'expression de la dissipation (<)
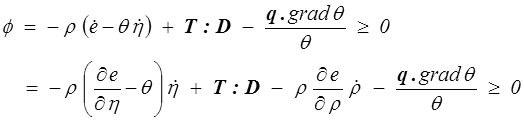
Soit finalement, en réutilisant les calculs déjà faits en MMC (<) ,
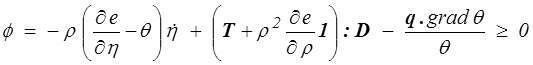
A la dissipation visqueuse déjà connue vient se rajouter la dissipation entropique que, comme toujours, nous supposerons nulle (<) et la dissipation thermique.
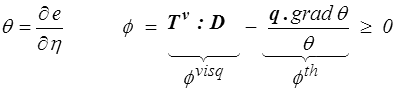
On peut également mener le calcul à partir de l'énergie libre
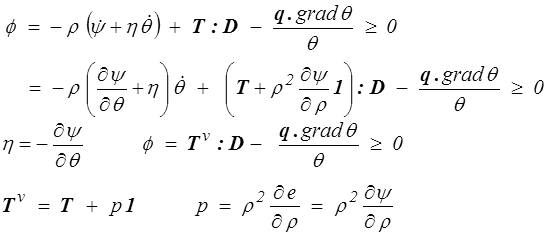
On notera toutefois que la pression p dépendra, outre la masse volumique, de l'entropie ou de la température, suivant que l'on préfèrera utiliser l'énergie interne ou l'énergie libre. Remarquons aussi que, puisque pour l'unité de masse V = 1 / ρ, cette relation coïncide bien avec les formules thermodynamiques classiques p = − ∂e / ∂V = − ∂ψ / ∂V.
Le fluide parfait
Pour un fluide parfait, la dissipation visqueuse est nulle, mais la dissipation thermique subsiste
T = − p ( ρ , η ) 1 ou − p ( ρ , θ ) 1
et pour déterminer la répartition de température ou d'entropie il faudra résoudre une équation de la chaleur (<) .
Si par contre les échanges de chaleur sont nuls ou négligeables
- pas d'apport volumique de chaleur, r = 0,
- fluide isolant, q = 0, ou parfaitement conducteur, grad θ = 0,
alors l'équation de conservation de l'énergie (<) se réduit à
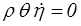
L'entropie reste constante et uniforme si elle l'a été à un moment ou à un autre. L'écoulement est isentropique. C'est une hypothèse courante en acoustique et la vitesse du son doit dans ce cas être calculée à partir de la loi d'état isentropique, soit par exemple pour un gaz parfait
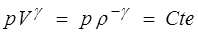
Le fluide visqueux
Dans le cas général nous revenons à la dissipation
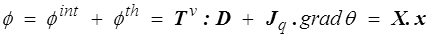
où les forces et les flux thermodynamiques X et x (<) sont
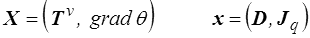
et on peut écrire les relations d'Onsager (<) qui finalement peuvent se mettre sous la forme
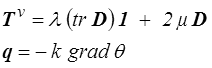
Il résulte en particulier des conditions de symétrie qu'il ne peut pas y avoir de couplage entre la conduction (phénomène vectoriel) et la viscosité (phénomène tensoriel). Plus généralement on admet souvent qu'il ne peut exister de couplage entre phénomènes vectoriels et tensoriels; on invoque alors traditionnellement le principe de Curie, mais c'est au mieux un abus de langage. Nous y reviendrons plus loin et je n'insiste pas pour l'instant..
La loi visqueuse compressible (<) est maintenant complétée par la loi de Fourier (<) . On obtient ainsi un système fermé d'équations (<) qui, avec des conditions initiales et aux limites thermiques et mécaniques, permettront de résoudre le problème thermomécanique.
