Tenseur des Contraintes
Contraintes de Cauchy
Tout ce qui a été dit précédemment sur la description des efforts (<) et la formulation de la loi fondamentale (<) reste d'actualité. Nous remarquons simplement que cette formulation est complètement eulérienne. C'est normal puisque la loi fondamentale, comme toute loi physique, s'applique dans l'espace physique réel; elle est par nature eulérienne.
Nous nous bornerons donc à un simple changement de notation et de terminologie. Le tenseur des contraintes σ est désormais le tenseur des contraintes de Cauchy (Eh oui, il y en aura d'autres !) et sera noté T. C'est un tenseur eulérien (rouge), il permet d'écrire la force élémentaire df exercée sur un élément de surface dS par
et la loi fondamentale (<) s'écrit de même
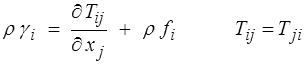
Ce tenseur est symétrique d'après la conservation du moment cinétique. Un changement de notation (et de couleur) donc mais rien de nouveau!
Formulation lagrangienne
Ainsi la formulation que nous avons donnée de la loi fondamentale est essentiellement eulérienne. Peut-on, comme pour l'équation de la masse (<) , en donner une formulation lagrangienne ? Pour cela il faut une version lagrangienne de l'équation de conservation de la quantité de mouvement (<) − et aussi de la conservation du moment cinétique, mais cela fonctionnera de la même manière −. Pour la quantité d'accélération par exemple
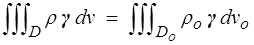
soit, mise en couleurs,
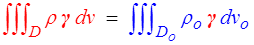
Voilà la difficulté : la conservation est bien écrite en variables lagrangiennes, mais la quantité dont nous écrivons la conservation est, elle, eulérienne. On procède de même pour les autres termes et on obtient (je vous laisse le soin de colorier)
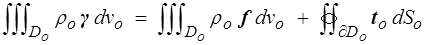
où to dSo représente la force élémentaire df (eulérienne puisque les forces agissent dans l'espace physique) exercée sur un élément de surface dSo de la frontière ∂Do du domaine lagrangien.
C'est en fait la formulation lagrangienne générale d'une loi de conservation et nous pourrions reproduire dans Do ce que nous avions fait dans D, et appliquer notre loi fondamentale lagrangienne à un disque (<) puis à un tétraèdre (<) − tous deux dans Do , mais peu importe − pour montrer que to dépend linéairement de la normale N à Do .
Premier tenseur de Piola-Kirchhoff
Nous pouvons plus simplement remarquer que cette force élémentaire df peut être calculée à partir du tenseur des contraintes de Cauchy
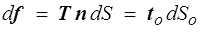
Attention à ne pas confondre le vecteur contrainte noté T jusqu'à présent et le tenseur des contraintes de Cauchy noté désormais T ; c'est pour cette raison que j'ai choisi de noter to et non To ce vecteur contrainte hybride (eulérien car dans la configuration actuelle, mais rapporté à la configuration de référence).
La formule de Nanson (<) donne alors directement
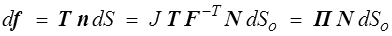
où nous avons introduit un nouveau tenseur des contraintes
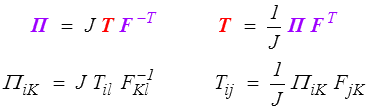
Ce tenseur Π est le premier tenseur de Piola-Kirchhoff (Eh oui, il y en aura un deuxième !), PK1 pour les intimes, ou parfois aussi, en francophonie, tenseur de Boussinesq.
Comme le tenseur F, c'est un tenseur mixte, mi-lagrangien mi-eulérien, non symétrique bien sûr : la symétrie n'aurait en fait aucun sens car on ne peut échanger les deux indices. Ce nouveau tenseur des contraintes peut sembler bien compliqué. Il est pourtant très naturel et porteur de sens physique. Il représente en effet la force par unité de surface avant déformation, soit, dans un essai de traction, F/So , c'est la contrainte nominale (<) , par opposition à la contrainte vraie F/S qui, elle, correspond au tenseur de Cauchy. Nous y reviendrons plus loin (>) .
Comme en formulation eulérienne, on réécrit ensuite la loi fondamentale
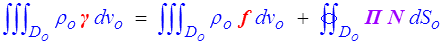
et par utilisation du théorème de la divergence dans Do on en tire l'équation du mouvement dans sa « version lagrangienne »
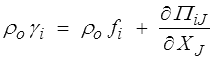
qui, comme on pouvait s'y attendre, n'est que très partiellement lagrangienne : la réalité physique persiste à rester eulérienne, seule sa description est lagrangienne. C'est encore plus vrai pour l'équation du moment cinétique qui, après maintes péripéties, finit simplement par donner
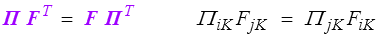
soit... la symétrie du tenseur de Cauchy.
Second tenseur de Piola-Kirchhoff
La formulation lagrangienne de la loi fondamentale nous a conduit au premier tenseur de Piola-Kirchhoff, tenseur mixte, mi-lagrangien mi-eulérien. On peut obtenir un tenseur des contraintes complètement lagrangien en ramenant la force df dans Co . Nous définissons donc
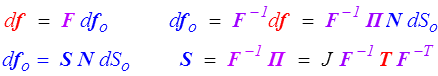
C'est le second tenseur de Piola-Kirchhoff (ou PK2)
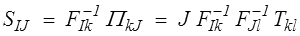
C'est un tenseur complètement lagrangien et symétrique, ce qui semblerait bien plus sympathique que PK1. Mais malheureusement et contrairement à PK1 il n'a, tout comme dfo qu'il permet de calculer, aucune signification physique.
Les tenseurs des contraintes
On peut donc utiliser, pour représenter les efforts intérieurs, trois tenseurs des contraintes
- le tenseur de Cauchy T (eulérien, rouge)
- le premier tenseur de Piola-Kirchhoff Π (mixte, violet)
- le second tenseur de Piola-Kirchhoff S (lagrangien, symétrique, bleu)
Nous en rajoutons un quatrième
- le tenseur de Kirchhoff τ = J T (eulérien, rouge)
et ces quatre tenseurs sont reliés par les relations
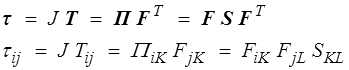
selon que l'on utilise les notations indicielles (<) ou tensorielles intrinsèques éventuellement colorisées (<) .
Est-ce tout ? Non ! Nous verrons plus tard que l'on peut en utiliser d'autres !
En petites perturbations
Dans le cadre de l'hypothèse des petites perturbations, le tenseur gradient reste voisin de l'identité. On aura par exemple au premier ordre
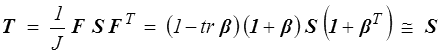
et de même pour les autres tenseurs.
Nous avons en grandes transformations introduit quatre tenseurs des contraintes différents, mais ces différences disparaissent (au premier ordre) en petites perturbations. Nous réserverons la lettre σ (en noir) pour cet usage, indiquant par là-même que nous nous plaçons en HPP.