Elasticité, viscosité, conduction
Un modèle générique
Pour aller plus loin il nous faut maintenant revenir sur le modèle proto-thermodynamique pour préciser les variables d'état correspondantes y. Nous avons déjà traité deux cas particuliers.
- En mécanique des fluides (<) y = J (ou ρ). Nous avons alors obtenu l'expression générale de la dissipation (<) qui nous a ensuite naturellement conduits aux différents modèles.
- Dans le cadre des petites perturbations (<) nous avions pris y = εij . Le calcul de la dissipation (<) nous a alors permis d'écrire les lois de la thermoélasticité.
Dans le cas général, la variable proto-thermodynamique de base sera un tenseur de déformation. Certes, mais lequel ?
Nous discuterons plus loin, en fonction du comportement que nous voulons décrire, quels sont les choix possibles. Nous nous limiterons ici au modèle générique obtenu en prenant simplement pour y le tenseur gradient de déformation F (<) . Comme nous l'avons déjà souligné, tout ce que nous ferons ici restera donc un peu formel puisque F contient à la fois les déformations et les rotations, alors que ces dernières ne peuvent pas être variables d'état. Cela restera à préciser en fonction des types de comportement envisagés.
Thermoélasticité
Pour la variable thermodynamique, nous préférons la température à l'entropie. Nous prendrons donc comme potentiel thermodynamique l'énergie libre ψ et nous partons de
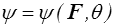
L'inégalité de Clausius-Duhem s'écrit, en utilisant pour ϖo int la forme mixte
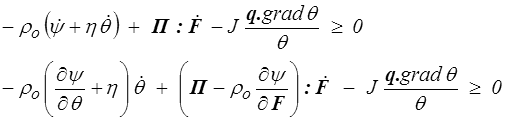
Le premier terme (dissipation entropique) sera toujours nul (<) . Les deux termes restants sont respectivement la dissipation visqueuse et la dissipation thermique.
En thermoélasticité, la dissipation visqueuse s'annule aussi et il ne reste plus que la dissipation thermique, inévitable sauf dans les deux cas limites, adiabatique (q = 0) et isotherme ( grad θ = 0 , θ uniforme). La loi élastique s'écrira donc
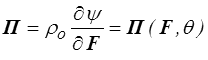
tandis que la conduction sera usuellement modélisée par la loi de Fourier
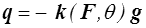
avec un tenseur de conductivité k
- symétrique (relations d'Onsager),
- pouvant éventuellement dépendre des variables d'état (F, θ).
Nous avons choisi pour cette loi de Fourier la formulation eulérienne, nous aurions tout aussi bien pu préférer une formulation lagrangienne, relation entre le flux de chaleur lagrangien Q et le gradient lagrangien de température
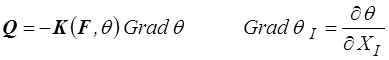
Peu importe en fait car le passage de l'une à l'autre (q, grad θ) ↔ (Q , Grad θ) se fait par le tenseur gradient F qui est justement dans la liste des variables. Rappelons encore que tout ce que nous faisons ici est correct mais partiel, et qu'il nous reste encore du travail pour préciser la dépendance en F.
On remarquera que l'on retrouve la loi élastique que nous avions obtenu par formalisme variationnel direct (<) . Ce modèle hyperélastique est en fait le modèle de base en élasticité grandes déformations
Modèle de Kelvin-Voigt
Dans le cas général, il faut également prendre en compte la dissipation visqueuse pour écrire de manière générale
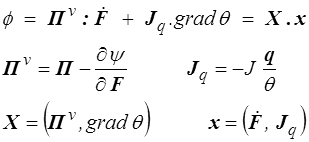
et la thermodynamique des processus irréversibles nous conduira à écrire une relation entre les forces et les flux. Contrairement à la conduction thermique, nous serons, pour la partie visqueuse, amenés à quitter le cadre linéaire pour aborder par exemple la viscoplasticité. Nous verrons cela plus tard, mais, même dans le cas linéaire, il est commode d'utiliser un potentiel de dissipation Ω (<) qui assurera automatiquement les relations de réciprocité d'Onsager, c'est-à-dire la symétrie de la matrice des coefficients phénoménologiques (<) . Nous écrirons donc
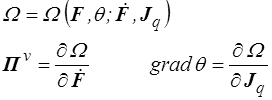
où le potentiel de dissipation Ω est, dans le cas linéaire, fonction quadratique des flux thermodynamiques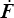 
, Jq mais peut aussi dépendre paramétriquement des variables d'état (F,θ). On remarquera qu'il serait ici plus naturel d'écrire Π v et Jq en fonction de 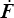et g = grad θ. On se retrouverait alors dans le cas de l'écriture mixte que nous avons décrit plus haut (<)
.
Cette formulation permet de prendre en compte un éventuel couplage entre viscosité et conduction. Nous aurons l'occasion de revenir plus loin sur cette éventualité. Si le couplage n'existe pas, alors
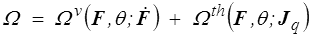
qui redonnera pour le volet thermique la loi de Fourier
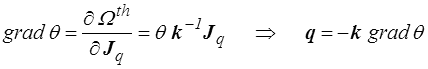
et pour la contrainte
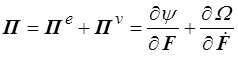
c'est-à-dire en HPP un modèle de type Kelvin-Voigt (<) , d'où le titre de ce paragraphe.
On remarquera que le fluide visqueux newtonien (<) rentre dans ce cadre.
Variables internes
Pour aller plus loin il nous faut introduire, dans l'énergie, des variables supplémentaires : les variables internes, que nous avons déjà présentées en HPP (<) . Pour décrire, à un instant donné, l'état thermodynamique du système, il faut rajouter aux variables observables (F,θ) des variables internes que nous noterons génériquement α.
Rappelons ici que le système thermodynamique considéré en MMC est local; c'est un petit élément de volume, suffisamment petit pour que les champs F(x,t) et θ(x,t) puissent être supposés constants. C'est l'hypothèse de l'état local (<) . Toutefois ce pourra être aussi un système macroscopique homogène, si l'on est capable de le réaliser expérimentalement comme on le fait dans les essais homogènes (<) .
On suppose donc l'énergie libre ψ(F,θ,α), et la dissipation s'écrira
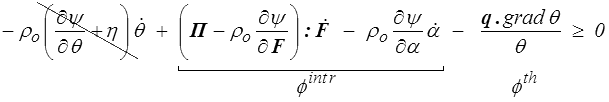
et nous pourrons, pour modéliser la dissipation intrinsèque, transposer directement tout ce que nous avons présenté en HPP.