Dualité Contraintes-Déformations
Vitesses de transformation
Le tenseur gradient de déformation décrit la transformation locale du vecteur matériel dX. Sa dérivée temporelle définira donc la vitesse de transformation
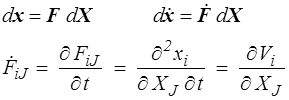
puisque, en description lagrangienne, les dérivées temporelle et spatiales commutent. La dérivée temporelle du tenseur gradient est donc aussi le gradient lagrangien des vitesses.
Le tenseur gradient des vitesses eulérien est, lui, défini par
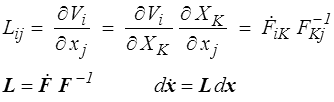
et on décompose ce tenseur eulérien L en partie symétrique D (tenseur des taux de déformation) et antisymétrique W (taux de rotation)
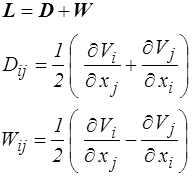
Ce tenseur caractérise le mouvement local et on peut directement transposer le calcul fait en HPP (<) pour décrire localement le champ des vitesses autour d'un point xo
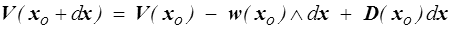
où w est le vecteur adjoint du tenseur antisymétrique W (<) .
Pour dégager la signification du tenseur des taux de déformation il suffit, là encore, de paraphraser tout ce dont nous avons discuté à propos du tenseur des déformations infinitésimales. Par exemple, la dérivée temporelle du produit scalaire de deux vecteurs matériels sera
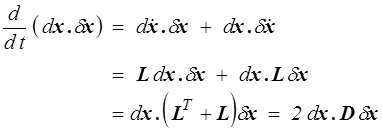
Ceci nous permettrait ensuite de définir vitesses d'allongement et vitesses de glissement. En travaillant sur les vitesses, on compare en fait deux configurations voisines C(t) et C(t+dt) , on est donc bien en HPP.
Dilatation sphérique et distorsion
On obtient, en dérivant par rapport au temps la décomposition en dilatation et distorsion (<) ,
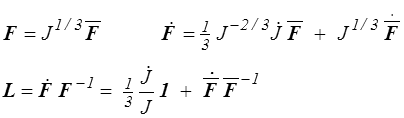
On vérifie sans peine que le second terme est de trace nulle (<)
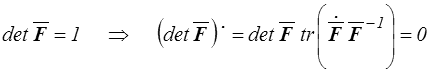
Cette décomposition de F correspond donc à la décomposition du tenseur taux de déformation en partie sphérique et déviateur
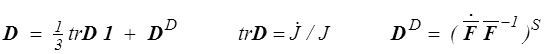
On pouvait s'y attendre : partant de la relation ρJ = ρo = Cte, on obtient par dérivation
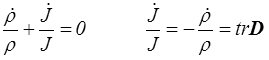
qui n'est rien d'autre que l'équation de continuité (<) .
Vitesses de déformation
Pour calculer la dérivée temporelle du produit scalaire de deux vecteurs matériels, on peut aussi partir de la formulation lagrangienne qui nous avait conduit au tenseur de Cauchy-Green droit C (<)
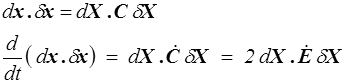
On en tire directement la relation entre C et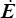 
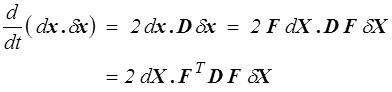
Cette relation peut aussi s'obtenir directement à partir de la définition de C
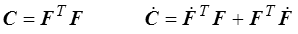
Mais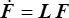 
et 
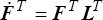donc
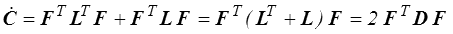
Les vitesses de déformation sont, en description lagrangienne, données par les dérivées temporelles du tenseur lagrangien des déformations. Rien de plus normal pourrait-on penser. Certes, mais cela ne marche pas en description eulérienne. Calculons par exemple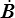 
et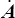 
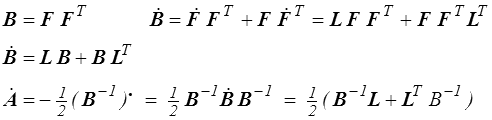
Les dérivées temporelles de B et A font donc intervenir le tenseur L tout entier, donc les deux tenseurs taux de déformation et de rotation. En particulier si les vitesses de déformation sont nulles, D = 0, L = W, il reste
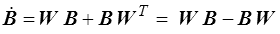
et 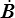n'est pas nul. En fait c'est la dérivation temporelle des tenseurs eulériens qui pose problème, nous y reviendrons.
Dérivation de la décomposition polaire
Le théorème de décomposition polaire (<) nous a permis d'extraire la rotation et la déformation du tenseur gradient F. Les taux de rotation et de déformation que nous venons de construire peuvent-ils être interprétés comme les taux de ces tenseurs ? La réponse est en général non. On aura par exemple par dérivation de la décomposition polaire
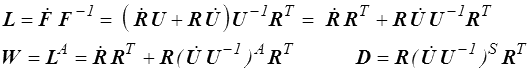
car le produit des deux tenseurs symétriques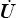 
et U −1 n'est pas symétrique.
De la même manière
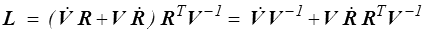
La dérivée temporelle du tenseur de rotation intervient dans le taux de déformation et vice-versa.
Toutefois, ce couplage disparaît si l'on utilise la déformation relative (<) Ft(τ) et sa décomposition polaire
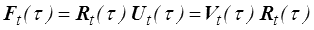
On pourra alors écrire en prenant comme référence la configuration C(t) et pour tout temps courant τ
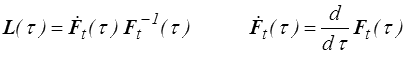
soit, par décomposition polaire,
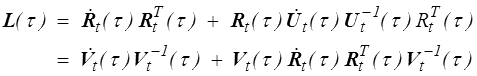
En prenant τ = t et en remarquant que
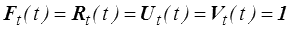
on obtient finalement
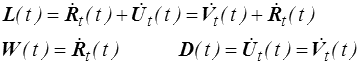
Les tenseurs taux de déformation et de rotation apparaissent donc bien comme les dérivées par rapport au temps des tenseurs de déformation pure (droit ou gauche) et rotation, mais seulement à condition de prendre comme référence la configuration à l'instant t considéré.
Puissance des efforts intérieurs
La puissance des efforts intérieurs est (<)
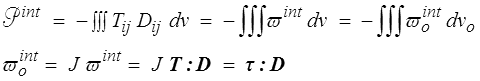
La quantité ϖoint est la puissance des efforts intérieurs par unité de volume dans la configuration de référence. On peut alors écrire, en utilisant les différents tenseurs des contraintes définis plus haut (<) ,
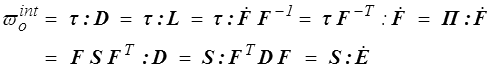
Ces différents tenseurs des contraintes apparaissent donc conjugués aux différents tenseurs susceptibles de décrire les vitesses de déformation
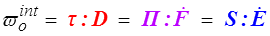
Les tenseurs D et 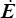mesurent en description eulérienne et lagrangienne respectivement les vitesses de déformation et ils sont naturellement conjugués aux tenseurs des contraintes de Kirchhoff (eulérien) et PK2 (lagrangien). Les tenseurs mixtes Π et 
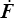sont également conjugués, mais 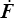fait intervenir en plus des taux de déformations les vitesses de rotation. Cette formulation mixte devra être utilisée avec précaution. Elle sera néanmoins fort utile (>)
.
Contraintes conjuguées de Seth-Hill
Plus généralement, on peut associer à chaque mesure des déformations un nouveau tenseur des contraintes, et on peut notamment associer aux mesures de Seth-Hill les tenseurs des contraintes conjugués par
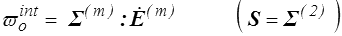
qui pour m = 2 redonne le second tenseur de Piola-Kirchhoff.
Si l'on souhaite utiliser les déformations de Seth-Hill, il semble assez naturel − et la thermodynamique nous confortera dans cette idée − de les mettre en relation avec ces nouveaux tenseurs des contraintes. Quelques modèles ont pu être proposés dans cette direction. Nous avons notamment constaté que l'utilisation des déformations logarithmiques (m = 0) présentaient bien des avantages (<) . Il est donc tentant d'utiliser systématiquement le tenseur de Hencky (<) et par conséquent le tenseur des contraintes conjugué Σ (o). Malheureusement, dans le cas général, on ne sait pas relier ces tenseurs Σ (m) aux tenseurs des contraintes usuels τ, T, Π ou S.
Le cas particulier m = 1 est une exception et on peut effectivement exprimer simplement le tenseur Σ (1) tel que
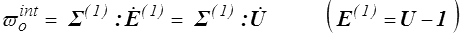
On obtient en effet à partir de la dérivation de la décomposition polaire (<)
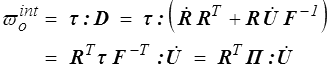
où l'on a utilisé la symétrie de τ, l'antisymétrie de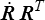 
et les règles de calcul sur les produits scalaires dans 
(<)
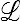. On en tire pour tout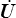 
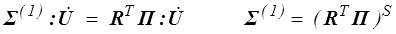
Ce tenseur est parfois appelé tenseur des contraintes de Biot.