Description de la transformation
Euler − Lagrange : le retour
Dans notre cours d'Introduction à la MMC (<) , la Mécanique des solides élastiques (<) et la Mécanique des fluides (<) suivaient des voies différentes mais qui les amenaient toutes deux à occulter leur point de départ commun, la description du mouvement : lagrangienne (<) ou eulérienne (<) .
- La mécanique des fluides est eulérienne par essence. Il y a toutefois, pour pouvoir ignorer Lagrange, un prix à payer : le terme convectif non-linéaire dans l'accélération (<) (techniquement ce prix est lourd, mais là n'est pas notre propos).
- La mécanique des solides classique peut, grâce à l'hypothèse des petites perturbations (<) , confondre Euler et Lagrange.
La voie est donc tracée pour englober ces deux mondes dans une synthèse unifiée, et y inclure du même coup le no-man's land qui les séparait : tous ces comportements intermédiaires (milieux viscoplastiques ou pâteux, fluides élastiques, etc.) dont nous avons déjà signalé l'importance, même pour des matériaux pourtant peu suspects de déviance (<) .
Il faut revenir à la source et, au lieu de chercher à la contourner, affronter de face la difficulté d'une double description
- eulérienne ou spatiale, car c'est là que se déroule l'action et que s'appliquent les lois de la physique,
- lagrangienne ou matérielle, car c'est la matière elle-même qui subit et contrôle cette action.
Configuration − Transformation
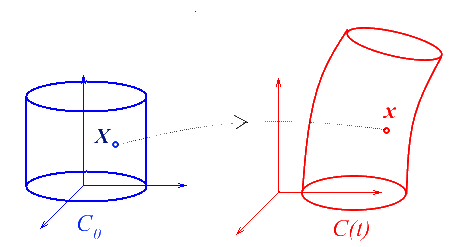
Dans une description continue, chaque point matériel ou particule sera identifié dans une « configuration de référence » Co. Une configuration quelconque C sera donc définie par une application
x = x ( X )
donnant dans cette configuration la position x de la particule X, cette application étant supposée continue, différentiable et inversible.
Le mouvement d'un milieu continu sera alors simplement l'ensemble des configurations occupées au cours du temps
x = x ( X , t )
Cette variable temps interviendra plus tard, mais je me borne pour l'instant à examiner le milieu continu dans une configuration donnée à un instant fixé (configuration actuelle).
La configuration de référence Co sert donc d'abord à identifier les particules pour pouvoir les suivre dans leur mouvement. La variable X joue en MMC le même rôle que le numérotage n = 1,... N pour un système de points matériels. Mais elle peut également servir d'étalon de référence pour C, la fonction x = x ( X ) définit alors la transformation faisant passer de Co à C (je préfère ici le mot transformation à déformation: nous verrons en effet que les rotations y jouent un rôle essentiel).
La configuration actuelle C est dans l'espace physique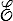 
(<)
et nous utiliserons pour la représenter un repère cartésien orthonormé de coordonnées xi ( i = 1,2,3 ). Nous ferons de même pour la configuration de référence Co avec des coordonnées XI ( I = 1,2,3 ) elles aussi cartésiennes orthonormées. (Rappelons ici que, sauf exceptions dûment signalées nous nous limitons aux repères orthonormés).
On choisit souvent comme configuration de référence Co la configuration C(0) occupée par le système à l'instant t = 0, mais cela n'a rien d'obligatoire. Il sera alors souvent commode d'utiliser le même système de coordonnées dans Co et C(t) (« référentiel du laboratoire »). C'est, pour mener les calculs, commode et tout à fait légitime, mais il est essentiel pour la suite de bien distinguer les deux. Dans la suite les indices latins minuscules seront toujours relatifs à la configuration actuelle C, tandis que les indices latins majuscules renvoient à Co.
Bien distinguer ce qui renvoie à Co (lagrangien) de ce qui renvoie à C (eulérien) est essentiel pour la compréhension des grandes transformations.
J'ai choisi de prendre comme référence une configuration Co possible du système − peu importe qu'il l'ait ou non occupée. Certains préfèrent utiliser une configuration abstraite − la variété matérielle souvent notée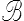 
, comme body − et éviter ainsi d'en privilégier une. On parle alors de placement plutôt que de transformation. C'est un choix respectable, mais j'ai préféré pour une première approche ne pas le faire.
D'un point de vue pratique et à condition de bien distinguer les deux systèmes de coordonnées xi et XI , le lecteur pourra, sans dommage majeur, se limiter au cas particulier Co = C(0).
Le tenseur gradient
La physique pourra être modélisée
- en description eulérienne, c'est-à-dire par rapport à la configuration actuelle C (rouge dans la suite) et dans le système de coordonnées xi,
- en description lagrangienne, c'est-à-dire par rapport à la configuration de référence Co (bleue dans la suite) et dans le système de coordonnées XI .
Chacune présente ses avantages et ses inconvénients ; nous les découvrirons dans la suite et nous verrons aussi que, selon ce que l'on cherche à faire, le choix de l'une ou l'autre s'impose assez naturellement.
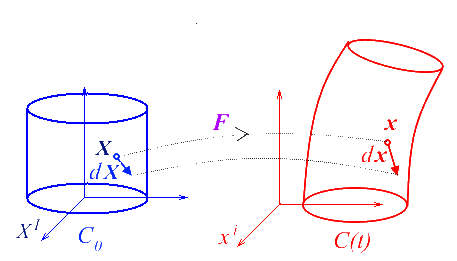
Il est donc essentiel de pouvoir passer de l'une à l'autre. Ceci se fera par l'intermédiaire du tenseur gradient (de la transformation) défini par
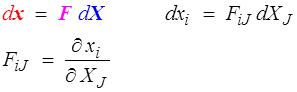
application linéaire qui au vecteur matériel (bleu) dX dans Co associe son transformé (rouge) dx dans C (application linéaire tangente). Ce tenseur sera inversible, et on définira
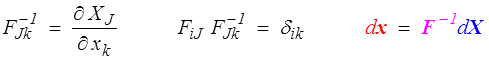
C'est une application linéaire de E − notre espace vectoriel euclidien (<) − dans E. C'est donc bien un tenseur au sens où nous l'avons défini (<) . Toutefois l'espace de départ est dans Co tandis que l'espace d'arrivée est dans C. Certains lui contestent même de ce fait la qualité de "tenseur" et préfèrent parler en anglais de "shifter" qui peut se traduire par "déplaceur"; il permet effectivement de "déplacer" un objet entre Co et C. On peut aussi garder à l'esprit l'image d'un tenseur ayant ses deux pieds dans deux configurations différentes. Attention alors aux entorses lorsque plus tard nous les ferons tourner.
Nous rencontrerons quelques autres tenseurs de ce type - peu nombreux mais importants - et nous les noterons en violet lorsque nous voudrons travailler « en couleur » (ce que je ferai assez souvent dans la suite : bien identifier ce qui est lagrangien ou eulérien est essentiel pour bien comprendre les grandes transformations et ce code de couleurs − bleu = lagrangien, rouge = eulérien − peut y aider. Plus de 30 ans après c'est la trouvaille pédagogique dont je reste le plus fier.)
Tensoriellement on pourra écrire
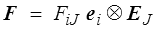
en notant ei et EJ respectivement les vecteurs de base des deux systèmes de coordonnées eulérien (xi ) et lagrangien (XJ ), tous deux choisis orthonormés, rappelons-le. On peut bien évidemment définir les tenseurs transposés
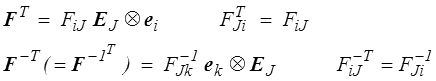
mais ils n'ont pour l'instant aucune signification géométrique.
Jacobien de la transformation
Le tenseur gradient permet de calculer le jacobien de la transformation
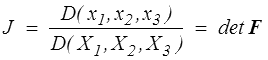
et donc la variation de volume dans la transformation
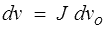
Il permet donc aussi de relier, pour une quantité quelconque, les densités volumiques lagrangienne et eulérienne (<)
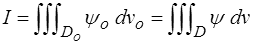
dont on tire directement
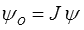
soit notamment pour la masse volumique
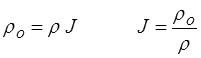
En particulier, un matériau incompressible (hypothèse très courante en grandes transformations) se caractérise par la liaison
J = 1
Formule de Nanson
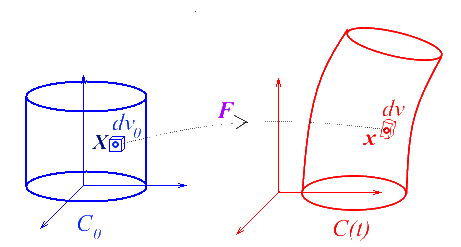
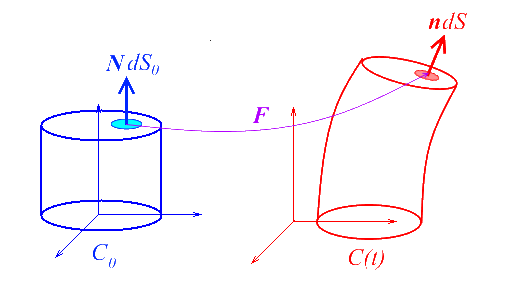On peut également tirer du tenseur gradient la transformation d'un élément de surface N dSo dans Co, qui devient n dS dans C (direction et aire de la surface).
Formule de Nanson.
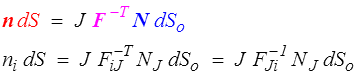
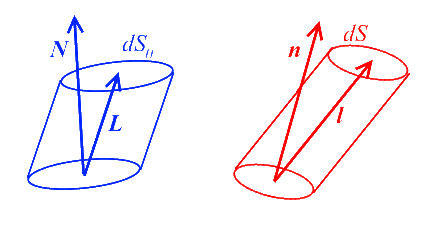Pour démontrer ce résultat, on considère dans C un cylindre élémentaire de base dSo et de génératrice L. Son volume dans Co est (base x hauteur)
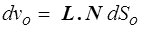
Après transformation dans C ce cylindre devient un cylindre de base n dS et de génératrice l = F L, son volume sera donc
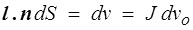
On aura donc
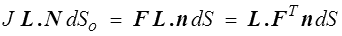
Ceci étant vrai pour tout vecteur L, on en tire
Le calcul qui précède est mené en notations tensorielles intrinsèques (<) . On pourra à titre d'exercice a/ le colorier b/ l'expliciter en notations indicielles classiques en prenant bien soin de distinguer les composantes lagrangiennes et eulériennes ( latines majuscules et minuscules respectivement) et
Le tenseur gradient caractérise la transformation locale, car il permet de suivre la transformation des éléments de longueur, surface et volume.
Transformation relative
Le choix de la configuration de référence est essentiel mais a priori arbitraire. Il importera donc d'intégrer dans nos développements ce qui se passe lorsqu'on en change.
Comme nous l'avons déjà signalé, il est souvent naturel, même si cela n'est pas nécessaire, de choisir pour Co la configuration C(to ) occupée par le solide à l'instant to qui sera souvent pris comme origine (to = 0), mais ce temps de référence est lui-même arbitraire. Il existe pour lever cet arbitraire une solution drastique : choisir comme configuration de référence pour étudier le système la configuration C(t) du système à ce même instant.
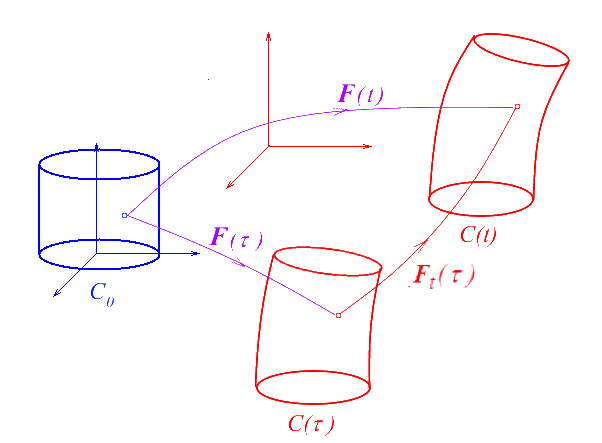
Pour définir dans ce cadre la configuration du système à l'instant τ (antérieur : τ < t, ou postérieur τ > t ) on écrira
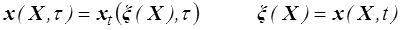
soit par dérivation
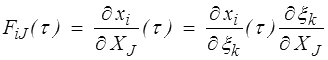
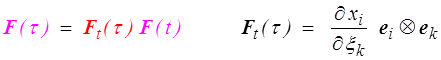
Le tenseur Ft (τ) est le gradient de la transformation relative C(t) → C(τ). Elle jouera un rôle important dans la suite, souvenons-nous simplement qu'elle correspond au choix de la configuration actuelle comme configuration de référence. (C'est en fait l'idée, populaire en mécanique numérique, de formulation lagrangienne réactualisée).
Remarquons que bien évidemment
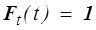
Dilatation sphérique et distorsion
Nous décomposons F
où J caractérise la variation de volume (dilatation sphérique) et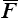 
une transformation sans changement de volume (distorsion).
Hypothèse des petites perturbations
Dans le cadre des petites perturbations (<) on écrira
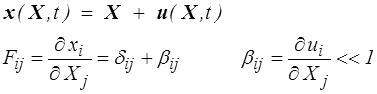
qui fait intervenir le tenseur β, gradient du déplacement (<) . On remarquera que dans ce cadre, puisque l'on identifie C à Co , il n'y a plus lieu de distinguer les coordonnées lagrangiennes et eulériennes, et donc les indices minuscules et majuscules. On pourra alors écrire au premier ordre
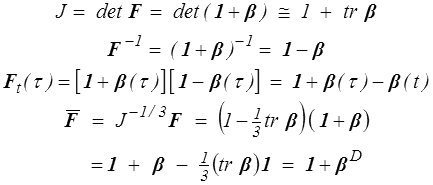
et la décomposition de F en dilatation sphérique et distorsion correspond, comme on pouvait s'y attendre, à la décomposition de β en partie sphérique et déviateur (<) .