Grandes Transformations en 2D
Animation
En bidimensionnel le tenseur gradient F fait intervenir 4 composantes
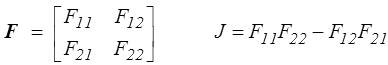
Le théorème de décomposition polaire donne le tenseur rotation et les 2 tenseurs de déformation pure droit et gauche
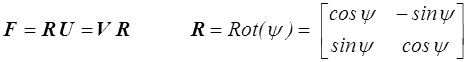
où ψ est l'angle de rotation et où Rot(ψ) représente l'opérateur linéaire de rotation par ψ.
Une animation permet de visualiser, en fonction de leur orientation, la déformation de deux vecteurs initialement perpendiculaires (et donc allongement et glissement). Elle illustre également la décomposition polaire. Vous pouvez la télécharger et vous trouverez ici comment l'utiliser.
Description canonique
Le tenseur de déformation pure U est symétrique défini positif et sera caractérisé par ses valeurs propres λ1, λ2 (allongements principaux ) et l'orientation θU de la direction principale associée à λ1. On pourra donc écrire
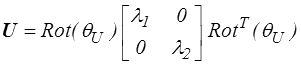
On peut de même écrire
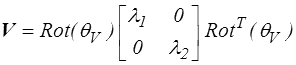
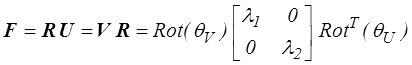
avec θV = θU + ψ.
Nous utiliserons maintenant les déformations principales logarithmiques et nous poserons
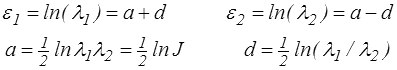
Une transformation 2D sera donc définie par 4 paramètres a, d, ψ et θo = θU
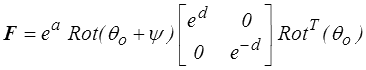
Les deux paramètres a et d caractérisent la dilatation uniforme et la distorsion, ψ la rotation propre et θo l'orientation des directions principales dans Co.
Rotation et allongement
Comme nous l'avons fait en petites déformations (<) nous partons d'un vecteur matériel dX dans la direction N, dX = dX N.
Le vecteur dx transformé s'écrit
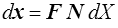
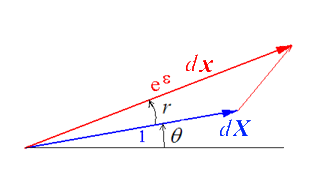Nous caractérisons cette transformation par son allongement logarithmique et sa rotation
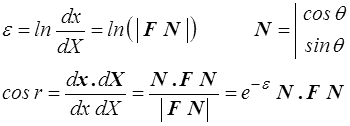
Et nous nous intéressons à l'évolution lorsque θ varie, du point représentatif − dans le plan ε, r, extension de la représentation de Mohr en grandes transformations (<) . Contrairement à ce qui se passait en HPP, ce vecteur (ε, r) n'a pas de signification géométrique. On peut toutefois lui trouver une interprétation algébrique dans le plan complexe en posant
On peut alors écrire
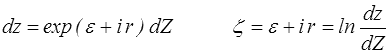
Pour calculer ε et r on part de la forme canonique et on remarque d'abord qu'il suffit de faire le calcul pour
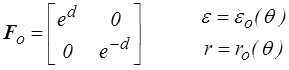
c'est-à-dire en prenant a = ψ = θo = 0. En notant εo(θ) et ro(θ) les fonctions correspondantes, la dépendance par rapport aux 3 autres paramètres de la forme canonique s'en déduira alors simplement par
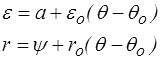
Il nous reste à déterminer ces deux fonctions εo(θ) et ro(θ).
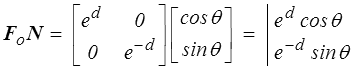
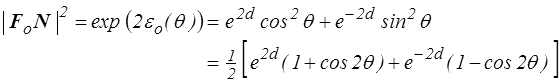
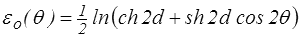
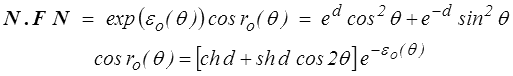
On obtient donc finalement
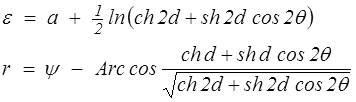
Cercloïde de Mohr
Lorsque θ varie le point représentatif (ε, r) décrit dans le plan de Mohr (généralisé) une courbe centrée en (a, ψ) et dont la forme dépend du seul paramètre d ≥ 0.
La figure ci-dessous représente cette courbe pour différentes valeurs de d.
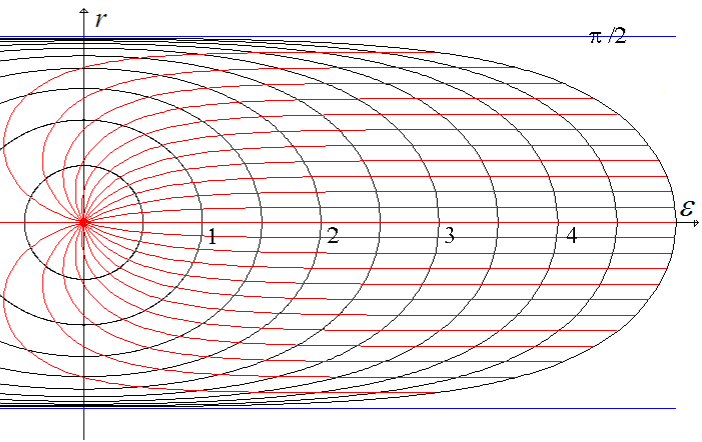
On constate qu'elle est doublement symétrique.
Pour d petit on retrouve le cercle de Mohr (<) . C'est normal car on peut alors écrire en notation complexe
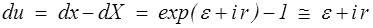
Lorsque d augmente on obtient une courbe de plus en plus aplatie : son demi-axe horizontal vaut d tandis que le demi-axe vertical est limité à π/2.
On a également représenté sur cette figure le réseau des courbes obtenues en fixant θ à d variable (courbes rouges).
L'équation de ces cercloïdes peut également, après quelques manipulations, se mettre sous une forme très concise
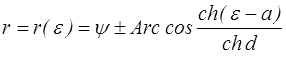
qui montre sa symétrie et permet de calculer en fonction de d son demi-axe vertical
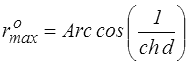
Pour obtenir cette forme il suffit d'éliminer θ entre les deux relations obtenues plus haut pour εo(θ) et ro(θ) (a = ψ = θo = 0)
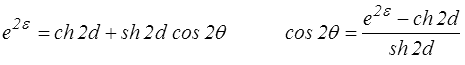
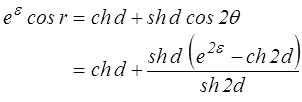
mais
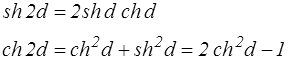
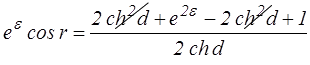
soit finalement
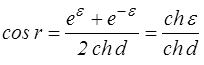
Une autre animation
Une animation vous est proposée pour illustrer cette notion. Elle vous permettra également de construire la description canonique en fonction de F. Vous pouvez la télécharger et vous trouverez ici comment l'utiliser.