Vecteurs et Tenseurs
La notion de tenseur est, en mécanique des milieux continus, essentielle, centrale et parfois intimidante. C'est, dans un cursus normal de physique, la première fois que vous les rencontrez de face et sans possibilité de contournement. (En fait nous en avez déjà rencontré, mais on avait jusque-là pu vous les cacher en les déguisant en vecteurs). J'ai coutume de dire que la difficulté essentielle en MMC n'est ni dans les mathématiques, qui ne dépassent guère le calcul matriciel et l'analyse élémentaire, ni dans la physique, newtonienne et macroscopique donc proche de notre expérience quotidienne, mais dans leur synthèse. C'est particulièrement vrai ici.
Lorsque l'on vous a introduit pour la première fois les vecteurs (actuellement en seconde je crois) tout cela a dû vous paraître bien abstrait et sans lien avec la vie réelle. Vous en avez je pense aujourd'hui une perception intuitive et leur signification physique vous est, je l'espère, familière. Eh bien, pour les tenseurs c'est pareil ! Un tenseur n'est en fait qu'une application linéaire (ou une forme bilinéaire), mais pour dépasser cette définition il vous faudra apprendre à le « voir ». Le tenseur des contraintes (>) est à cet égard l'exemple de référence et c'est là tout l'intérêt de leurs représentations géométriques et notamment du cercle de Mohr (>) . Ne négligez pas cet effort de perception et d'apprivoisement. C'est à mon avis l'une des clefs d'une vraie compréhension de la MMC.
Mon objectif dans cette page est double.
- Introduire (rapidement) les résultats et notations essentiels. Je renvoie toujours au polycopié (poly annexe A) pour une présentation un peu plus détaillée.
- Proposer quelques éclairages, ouvertures et pistes de réflexion pour mieux appréhender ces objets, je le répète, essentiels.
Il n'est ni nécessaire, ni même recommandé, de chercher à maîtriser d'emblée l'ensemble de cette page. Je vous invite par contre à y revenir régulièremnt. C'est en les manipulant que vous vous approprierez ces notions.
Espace, vecteurs, repères et champs
Avant de rentrer dans le vif du sujet, il peut être utile de préciser quelques points de terminologie.
Nous travaillons dans l'espace tridimensionnel euclidien qui nous est familier (ne serait-ce que parce que nous y vivons − du moins à notre échelle terrestre −). Il importe toutefois de bien distinguer cet espace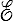 
(affine pour le mathématicien) de l'espace vectoriel sous-jacent E. Une fois choisie une origine, mais ce choix est arbitraire, on peut identifier 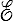à E en identifiant un point M de 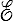au vecteur OM ∈ E. Ce n'en sont pas moins deux espaces différents et leur confusion peut conduire à bien des incompréhensions. Une fois choisie une base de E on en tire un repère de 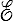, chaque point étant repéré par ses coordonnées, c'est-à-dire les composantes du vecteur OM dans la base choisie. On parle alors d'un repère cartésien.
Notre espace euclidien est muni d'un produit scalaire, et donc sur E d'une norme et sur 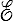d'une distance. Nous choisirons alors une base orthonormée de E conduisant sur 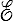à un repère orthonormé. Ce choix est essentiel car sinon les choses deviendraient techniquement beaucoup plus compliquées. Il pourra être utile de délaisser les coordonnées cartésiennes pour travailler en coordonnées curvilignes (>)
(cylindriques ou sphériques le plus souvent), mais à condition de n'utiliser que des bases orthonormées. Et s'il nous fallait quitter ce cadre (c'est par exemple le cas en relativité ou plus près de nous en théorie des coques) la géométrie différentielle deviendrait un préliminaire incontournable.
En mécanique des milieux continus toutes les grandeurs physiques seront décrites par des « champs » c'est-à-dire des quantités scalaires (température, masse volumique, pression), vectorielles (vitesses, forces électriques ou gravitationnelles, flux de chaleur) ou tensorielles (contraintes, déformations) fonctions des variables d'espace et du temps.
Notations indicielles
Nous noterons xi = ( x1, x2, x3 ) notre système de coordonnées cartésiennes (sauf mention explicite du contraire) et orthonormées (toujours). Nous noterons ei , les vecteurs de base correspondants. On pourra donc écrire un vecteur V comme
V = V1 e1 + V2 e2 + V3 e3 = Vi ei
où nous adopterons systématiquement la convention de sommation : dans tout terme il faut faire la sommation par rapport aux indices répétés ; on parle d'indice « muets » car on peut à volonté changer leur nom. Par opposition, les indices « libres » caractérisent la ou les composantes concernées et on doit retrouver les mêmes dans chaque terme d'une égalité. On écrira ainsi par exemple une relation scalaire
a . b = ai bi ( = a1 b1 + a2 b2 + a3 b3 )
ε(n) = εij ni nj
une relation vectorielle (1 indice libre)
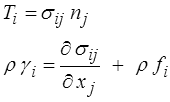
et nous écrirons plus tard une relation
σij = Aijkl εkl
avec deux indices libres i et j, et au second membre deux indices muets k et l.
On représente donc par cette simple formule 9 relations impliquant au second membre la somme de 9 termes. Que penser alors de cette autre relation que nous verrons bientôt
A'ijkl = Qim Qjn Qkp Qlq Amnpq
Ainsi, si dans un terme un indice apparaît
- 1 fois : c'est un indice libre,
- 2 fois : c'est un indice muet,
- 3 fois ? C'est une erreur assez courante lorsque l'on débute. Vérifiez toujours la cohérence indicielle de vos formules et de vos résultats.
Attention il est dans ce contexte assez délicat de manipuler les valeurs propres. Par exemple on peut écrire un tenseur symétrique (les contraintes par exemple) sous forme spectrale
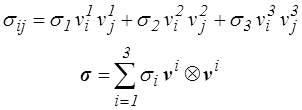
où σi sont les valeurs propres et v1, v2, v3 une base orthonormée de vecteurs propres. Diverses notations existent permettant de gérer cette dernière relation avec la convention de sommation, mais je vous conseille plutôt de les éviter.
Tenseurs
Un tenseur d'ordre 1, c'est un vecteur. Une fois choisie une base (orthonormée), il sera représenté par ses trois composantes Vi (i = 1,2,3) formant un « vecteur colonne » que nous dénoterons, lorsque ce sera nécessaire, par un souligné
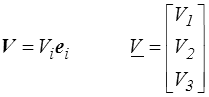
Le produit scalaire de deux vecteurs pourra alors s'écrire (repère orthonormé)
u . v = ui vi = uT v
Un tenseur d'ordre 2, c'est par exemple une application linéaire E → E qui à un vecteur x associe un vecteur y. Une fois choisie une base, elle sera représentée par une matrice
y = A x yi = Aij xj y = A x
Ce peut aussi être une forme bilinéaire qui à deux vecteurs x et y associe un scalaire A(x,y) que l'on peut, dans un espace euclidien, identifier à une application linéaire
A(y,x) = y . Ax = Aij yi xj = yT A x
Nous noterons assez systématiquement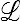 
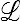= (E,E) l'espace des tenseurs d'ordre 2 et 
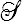l'espace des tenseurs symétriques.
Un tenseur d'ordre 4, ce sera par exemple une application linéaire de 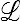dans 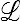qui à un tenseur a associe un autre tenseur b
bij = Mijkl akl
les matrices ne suffisent alors plus.
Nous pourrons rencontrer − plus rarement en MMC, mais cela pourra arriver − des tenseurs d'ordre 3, application linéaire de 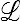dans E, ou bien de E dans 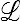, ou encore forme tri-linéaire associant un scalaire à 3 vecteurs ou bien... On rencontre même des tenseurs d'ordre 8. Les notations indicielles nous permettront en fait de manipuler sans difficulté des tenseurs d'ordre quelconque.
Pour être complet, il faut aussi évoquer le produit tensoriel. Par exemple, le produit tensoriel de 2 vecteurs u et v est le tenseur d'ordre deux qui, comme application linéaire M, est défini par
M = u ⊗ v
M x = u (v . x)
Mij = ui vj M = u vT
On notera la différence entre ce produit matriciel d'un vecteur colonne (matrice 3x1) par un vecteur ligne (matrice 1x3), définissant donc une matrice 3x3, avec la forme vue plus haut pour le produit scalaire u . v, produit matriciel d'un vecteur ligne par un vecteur colonne et conduisant donc à un scalaire.
Avec ces notations les produits tensoriels des vecteurs de base définissent une base dans l'espace des tenseurs
A = Aij ei ⊗ ej
Ces notations indicielles (jointes à la convention de sommation) sont une manière économique et efficace de gérer les relations parfois complexes que nous rencontrerons. Ne vous effrayez pas, c'est juste un réflexe à prendre.
Changement de repère et rotation
Les composantes d'un vecteur ou d'un tenseur dépendent de la base choisie, et changent lorsqu'on en change. Un changement de base pour passer d'une base ei à une base e'j est défini par la matrice de changement de base, matrice orthogonale si les deux bases sont orthonormées,
e'i = Qij ej ei = Qki e'k
Q QT = QT Q = 1 Qij Qik = Qji Qki = δjk
où l'on a introduit les symboles de Kronecker δij = 1 si i = j, δij = 0 si i ≠ j.
On en tire directement les formules de changement de repère pour un vecteur, un tenseur d'ordre deux ou d'ordre quelconque
V'i = Qij Vj
a'ij = Qik Qjl akl
A'ijkl = Qim Qjn Qkp Qlq Amnpq
D'ailleurs il serait plus précis de parler de changement de base, le changement de repère dans sous-entend aussi un changement d'origine, qui ne joue ici aucun rôle puisque nous travaillons dans l'espace vectoriel E et non dans l'espace affine .
On notera que pour un vecteur ou un tenseur d'ordre deux on peut écrire ces relations sous forme de produit matriciel
V' = Q V a' = Q a QT
mais cela ne marchera plus au-delà.
Remarquons que contrairement aux matrices introduites plus haut, composantes d'un tenseur sur une base, cette matrice de passage est bien au départ définie en tant que telle et sans se rapporter à un tenseur d'ordre deux. Toutefois on peut ensuite considérer le tenseur Q représenté dans la base originale ei par la matrice de passage transposée
Q = Qji ei ⊗ ej
et on vérifie que ce tenseur est l'application linéaire correspondant à la rotation qui fait passer de la base ei à la base e'i. Dans la suite nous confondrons assez souvent les deux notions (matrice de passage et tenseur rotation). Ainsi le vecteur V' et le tenseur a' définis par
V' = Q V a' = Q a QT
représenteront le vecteur V et le tenseur a tournés par Q.
Ces formules de changement de repère sont également utiles pour déterminer si un système de quantités obtenues d'une manière ou d'une autre sont ou ne sont pas les composantes d'un vecteur ou d'un tenseur. On parle alors de critère de tensorialité.
Permutations et déterminant
Pour pouvoir dans ce cadre traiter produit vectoriel et produit mixte, nous devons introduire les symboles de permutation ou de Levi-Civita
∈ijk = +1 si i, j, k est une permutation paire de 1,2,3,
= − 1 si permutation paire,
= 0 si deux indices sont égaux.
On vérifie alors directement que le produit vectoriel de deux vecteurs et le produit mixte de trois vecteurs sont respectivement donnés par
(a∧b)i = ∈ijk aj bk
(a,b,c) = ∈ijk ai bj ck
On vérifie aussi les formules suivantes
∈ijk ∈imn = δjm δkn − δjn δkm
∈ijk ∈ijl = 2 δkl
A titre d'exemple on peut obtenir ainsi la formule classique du double produit vectoriel
a ∧ (b ∧ c) = (a . c) b − (a . b) c
En effet la composante i du double produit est
∈ijk ∈kmn aj bm cn = (δim δjn − δin δjm) aj bm cn = bi aj cj − ci aj bj
Ces symboles permettent aussi de calculer le déterminant d'une matrice et sa matrice inverse par les formules
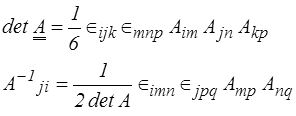
Tenseurs antisymétriques
Dans l'espace de dimension 3, un tenseur du second ordre antisymétrique fera intervenir 3 composantes indépendantes (Ω11 = Ω22 = Ω33 = 0, Ω12 = − Ω21 ,...). Soit en posant
définissant, dans la base choisie, le vecteur ω adjoint du tenseur antisymétrique
En particulier
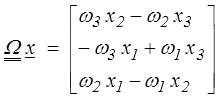
Donc tensoriellement
Ω x = − ω ∧ x
Chaque fois qu'interviendra un produit vectoriel ce sera en fait un tenseur antisymétrique masqué. Ce sera notamment le cas pour le vecteur rotation (<) et pour le moment d'une force(<), correspondant en fait aux tenseurs antisymétriques
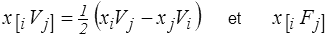
où nous avons utilisé une notation classique pour la décomposition d'un tenseur en partie symétrique et antisymétrique.
Nous n'utiliserons pas ou peu cette notation, mais vous pourrez la rencontrer
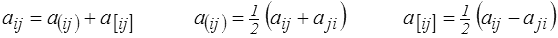
Ce « vecteur » n'en est pas tout à fait un. On constate en effet que dans un changement de repère ses composantes se transforment par
ω' = (det Q) Q ω
où det Q = ± 1 selon l'orientation relative des deux bases. Ses composantes ne se transforment comme celles d'un vecteur que pour les changements de base conservant l'orientation de l'espace.
On parle souvent de pseudo-vecteur ou de vecteur axial, mais ce sont en fait des tenseurs déguisés en vecteur.
Un autre exemple, plus spectaculaire encore, nous vient de l'électromagnétisme. On sait en effet que la force exercée sur une particule chargée est, à partir des champs électrique E et magnétique B, donnée par
F = q [ E + V ∧ B ]
On sait maintenant que le champ magnétique, vecteur axial, est en fait un tenseur antisymétrique, mais on peut aller plus loin dans l'espace-temps (c'est-à-dire en considérant le temps t comme une quatrième composante xo) en écrivant simplement
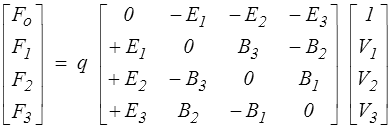
où la composante temporelle Fo se trouve être au signe près la puissance mécanique de la force F.
Les 6 composantes des deux vecteurs E et B sont en fait les composantes d'un tenseur antisymétrique dans l'espace-temps (tenseur électromagnétique qui ne prendra tout son sens que dans un contexte relativiste).
Dérivation et Intégration
Dans un modèle continu les différentes grandeurs physiques seront donc représentées par des champs de tenseurs d'ordres divers (0 pour les scalaires, 1 pour les vecteurs, ou 2..., rarement au-delà). La dérivation par rapport aux variables d'espace introduit les opérateurs classiques de l'analyse vectorielle qui en coordonnées cartésiennes s'expriment simplement par dérivation des composantes. Pour un champ scalaire f, on définit son gradient (vecteur) et son laplacien (scalaire) par
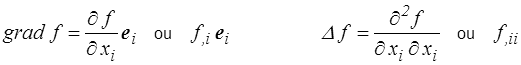
(on note assez souvent la dérivation par une virgule, c'est une notation parfois commode, mais que nous n'utiliserons que modérément). La convention de sommation s'applique bien évidemment aussi à ces indices de dérivation.
Pour un champ vectoriel, on définit de même sa divergence (scalaire), son rotationnel (vecteur) et son laplacien (vecteur)
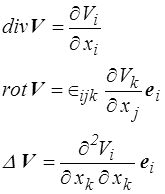
On pourra à titre d'exercice, et en utilisant les formules données plus haut (<) , démontrer la formule classique
Δ V = grad(div V) − rot(rot V)
ainsi que diverses autres formules (poly annexe A).
Dans la pratique, les notations indicielles remplacent avantageusement l'opérateur ∇ souvent utilisé en physique, mais qui demande davantage de précaution sitôt que l'on a des tenseurs. Par exemple l'expression eulérienne de l'accélération (<)
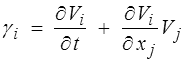
s'écrit aussi souvent sous la forme
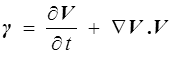
mais encore faut-il se souvenir de l'ordre des indices
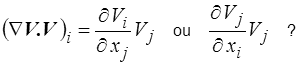
Les notations indicielles évitent ici toute ambiguïté.
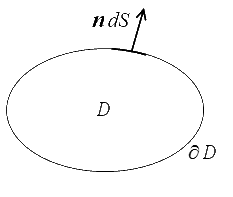
On sera de même amené à intégrer dans un volume et il sera souvent nécessaire de transformer ces intégrales. Nous utiliserons fréquemment le théorème suivant.
Théorème.
Si φ est une fonction continue et dérivable dans un domaine D alors
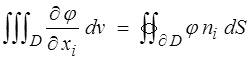
où ni est la normale extérieure à D sur la frontière ∂D de D.
Cette formule est souvent appelée théorème de la divergence (par abus de langage, le vrai théorème de la divergence correspond au cas particulier φ = Vi). Elle permettra de transformer les intégrales de volume en intégrales de surface.
Coordonnées curvilignes
Tout ce qui précède suppose un repère cartésien: on utilise en tout point x (de l'espace affine) la même base ei de E (espace vectoriel). Or il est parfois utile de travailler en coordonnées curvilignes (orthogonales, pour pouvoir encore utiliser en chaque point une base orthonormée). Cela ne change rien aux relations tensorielles locales mais exige sitôt qu'interviennent des dérivées, de dériver aussi les vecteurs de base. Dans la pratique, on utilisera des formulaires donnant l'expression des équations de la MMC (c'est-à-dire en fait les équations du mouvement et l'expression des déformations ou vitesses de déformation) en coordonnées curvilignes, notamment en coordonnées cylindriques et en coordonnées sphériques ===>