Rappel de thermodynamique
Premier principe
En thermodynamique classique on écrit usuellement le premier principe sous la forme
d U = đ W + đ Q
La variation de l'énergie interne du système est la somme du travail et de la chaleur qui lui sont apportés.
- d U est la différentielle de l'énergie interne U, fonction d'état extensive (c'est-à-dire, pour un système homogène, proportionnelle à la quantité de matière) et additive (l'énergie d'un système composé est la somme de celles de ses sous-systèmes).
- đ W est le travail fourni au système, sa forme précise dépendra du cadre mécanique ( - p dV pour un fluide, F dl pour une éprouvette en traction) ou physique ( E dD en électrostatique). Pour pouvoir faire de la thermodynamique sur un système il faut déjà avoir les idées claires sur sa physique hors thermodynamique (« modèle proto-thermodynamique »).
- đ Q est la chaleur fournie au système. C'est la nouveauté, et là, on commence à faire de la thermodynamique.
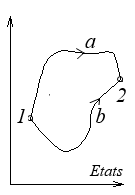D'un point de vue mathématique d U est la différentielle totale exacte d'une fonction d'état, tandis que đ W et đ Q sont des formes différentielles non intégrables, c'est-à-dire dont l'intégrale dépend du chemin suivi pour aller d'un état 1 à un état 2.
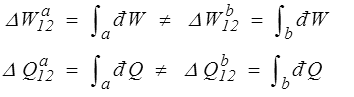
mais
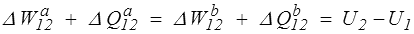
Le barreau en traction
Etat ? Chemin ? Tout cela est bel et bon, mais de quoi parle-t-on au juste ?
La thermodynamique classique s'intéresse à un système homogène dont l'étude physique proto-thermodynamique a permis de dégager
- les variables significatives,
- l'expression du travail đ W .
L'exemple classique est celui du fluide thermodynamique pour lequel les variables significatives sont la pression p et le volume V, avec
đ W = − p dV
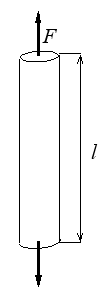Pour nous rapprocher de la mécanique des matériaux (mais aussi pour sortir de notre zone de confort en nous affranchissant de ce modèle peut-être trop connu) je prendrai plutôt comme modèle de base un barreau en traction. Les variables proto-thermodynamiques sont la force F de traction et la longueur l
đ W = F dl
et une loi de comportement permettra de relier F à l.
Pour greffer la thermodynamique, il faut d'abord introduire une nouvelle variable thermodynamique, typiquement, et pour commencer, une température θ telle qu'on la mesure avec un thermomètre.
Dans le modèle le plus simple, l'état thermodynamique de notre barreau est alors défini par ses deux variables d'état l et θ. Le premier principe s'écrit alors
d U = F dl + đ Q
où l'énergie interne est une fonction d'état, c'est-à-dire une fonction des variables d'état l et θ.
Cette description dépend de la quantité de matière. Pour neutraliser cette dépendance, nous choisissons pour notre barreau une configuration de référence (longueur lo, section So, volume Vo = So lo) et nous réécrivons
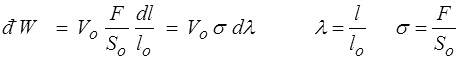
Les thermodynamiciens font grand cas de la distinction entre variables intensives (indépendantes de la quantité de matière, comme pression, température) et variables extensives (proportionnelles à la quantité de matière, comme volume, énergie). Cette distinction n'est ici pas si évidente puisque la variable extensive associée à la variable intensive σ serait
Vo λ = So l
qui n'est pas véritablement pertinente. Nous travaillerons plutôt sur les deux variables σ et λ, ce qui revient à considérer les quantités par unité de volume Vo. Le premier principe s'écrira alors
du = σ dλ + đq ( U = Vo u đ Q = Vo đq )
Second principe
Le premier principe est un principe d'égalité : l'énergie se transforme mais elle se conserve. Toutes ses formes sont énergétiquement équivalentes (rappelez-vous, le point de départ de tout cela, c'est l'équivalent mécanique de la chaleur: 1 kcal = 4,18 J ).
Le second principe vient amender ce principe d'égalité : toutes les formes d'énergie sont équivalentes mais elles ne se valent pas ; il est facile de transformer le travail en chaleur, l'inverse est beaucoup plus difficile.
Après quelques "péripéties" ce principe conduit finalement à l'introduction, à côté de l'énergie interne, de deux nouvelles fonctions d'état
- l'entropie S, variable extensive,
- la température absolue T, variable intensive.
Second principe.
Pour une évolution réversible
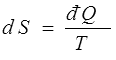
Pour une évolution irréversible
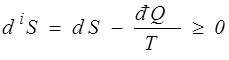
En termes mathématiques : La forme différentielle đ Q donnant la quantité de chaleur pour une évolution réversible n'est pas intégrable, mais elle admet un facteur intégrant, 1/T.
Nous utiliserons désormais, plutôt que la température thermométrique θ, la température absolue T. Rappelons que la température absolue se mesure en K (kelvin, unité SI ; on parle souvent de degré Kelvin ou °K, mais c'est incorrect). Dans la pratique on écrira simplement
T en K = θ en °C + 273.15
Le barreau thermoélastique
Revenons à notre barreau en traction et supposons que ce système est réversible (toutes les évolutions sont réversibles ; c'est l'analogue du fluide thermodynamique). On peut alors écrire
d U = F dl + T dS
ou en travaillant sur un volume Vo unité
du = σ dλ + T ds S = Vo s
Et plutôt que de considérer u comme une fonction de λ (ou l ) et de T, il est préférable de le considérer comme fonction de λ et de s. C'est un simple changement de variable mais qui permet d'écrire
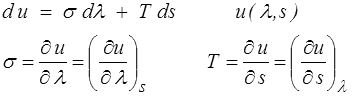
On dit que l'énergie interne u(λ,s) est un potentiel thermodynamique, ce ne serait pas le cas pour la fonction u(λ,T). En thermodynamique il est important, lorsqu'on écrit des dérivées partielles, de bien savoir de quelle fonction on parle (c'est ce que rappelle l'indice inférieur derrière la parenthèse, sage précaution !).
En utilisant s plutôt que T on a donc gagné un potentiel thermodynamique, mais on y a perdu en sens physique : on ne sait pas mesurer directement l'entropie !
Une transformation de Legendre permet de revenir à la température : l'énergie libre ψ est définie par
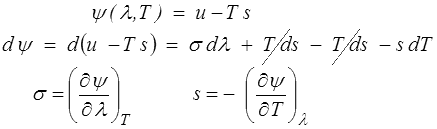
L'énergie libre ψ(λ,T) est aussi un potentiel thermodynamique. Attention toutefois à ne pas oublier que cette énergie libre est une construction mathématique sans signification énergétique directe. Elle sera souvent commode, mais, contrairement à l'énergie interne, ce n'est pas une grandeur physique première.
On construirait de la même manière l'enthalpie h et l'enthalpie libre g
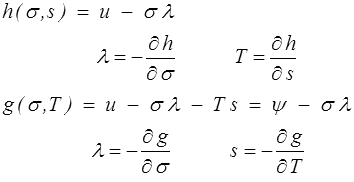
En jouant sur ces fonctions et leurs dérivées partielles on peut alors introduire diverses caractéristiques (coefficient de dilatation et de compressibilité, chaleurs spécifiques à déformation ou contrainte constante, etc...). La thermodynamique d'un barreau réversible est toute entière contenue dans l'un ou l'autre de ces quatre potentiels thermodynamiques.
Prise en compte de la dissipation
Dans une évolution irréversible le second principe s'écrira (toujours par unité de volume)
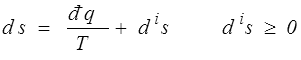
La variation de l'entropie du système est égale à l'apport extérieur d'entropie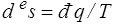 
plus la production interne d'entropie, toujours positive ou nulle. C'est l'essence même du second principe qui exprime en fait la non-conservation de l'entropie. Nous réécrirons, en utilisant le premier principe,
ou, en divisant par dt pour passer aux vitesses et puissances,
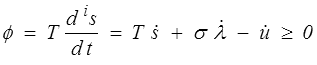
où la quantité ϕ, appelée dissipation, représente la production interne d'entropie, nulle pour une évolution réversible, et positive pour une évolution irréversible.
Pour aller plus loin, il faut faire quelques hypothèses, notamment sur l'énergie interne u. Le modèle dissipatif le plus simple s'obtiendra en gardant la même énergie que dans le modèle thermoélastique u(λ,s). Il vient alors
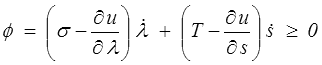
et nous nous retrouvons au point de départ de la thermodynamique des phénomènes irréversibles (<) avec potentiellement deux sources de dissipation. La première est mécanique et nous la connaissons déjà, c'est la dissipation visqueuse. La seconde est nouvelle, nous pourrions l'appeler la dissipation entropique. On écrira donc dans le cadre de la TPI
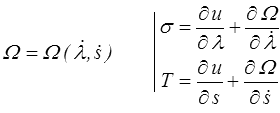
A une exception près peut-être (je crois avoir vu un jour passer un modèle contre-exemple, mais je n'en suis même plus certain) on suppose toujours que cette « dissipation entropique » est nulle, ce qui nous ramène directement à un modèle de Kelvin-Voigt (<) généralisé (non linéaire) complété par la relation thermodynamique classique pour la température
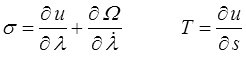
On passe alors immédiatement à l'énergie libre ψ = u − T s pour réécrire la dissipation sous la forme
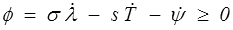
donc si ψ(λ,T)
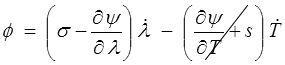
Et c'est tout ce que l'on peut faire avec ces variables d'état (λ,s) ou (λ,T). Pour aller plus loin il faudra, comme nous l'avons fait dans le cours de comportement, introduire, en plus des variables observables λ, s ou λ, T, des variables internes d'état (<) .