Tenseur des déformations
Green-Lagrange et Almansi
Comme en petites perturbations (<) les déformations correspondent aux variations de longueur et d'angle. Leur description passera par les variations de produit scalaire de deux vecteurs matériels.
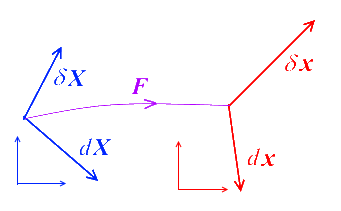
C'est, aux notations près, le même schéma qu'en HPP (<) avec toutefois une différence notable : les déformations étaient alors exagérées, elles ne le sont plus maintenant.
Le calcul (partiellement colorisé à nouveau) est simple.
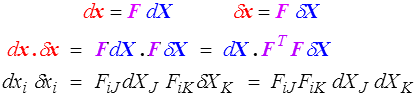
Nous définissons ainsi le tenseur des dilatations
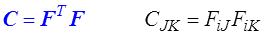
La variation de produit scalaire sera donc
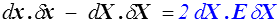
où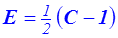 
est le tenseur des déformations de Green-Lagrange. C'est un tenseur lagrangien.
Son pendant eulérien s'obtiendra en caractérisant cette variation de produit scalaire à partir des vecteurs eulériens dx et δx
définissant le tenseur A d'Euler-Almansi. Le tenseur A se calcule facilement
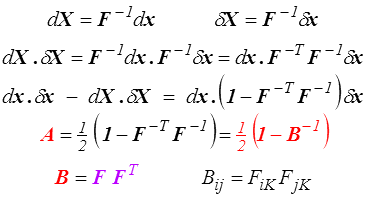
On aurait aussi pu écrire
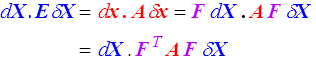
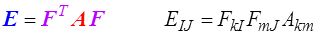
En comparant ces deux relations avec le cas des petites perturbations (<) on voit que les deux tenseurs E et A sont deux tenseurs (E lagrangien, bleu ; A eulérien, rouge) mesurant les déformations et on les calculera en passant par les deux tenseurs
respectivement appelés
C : tenseur de Cauchy-Green droit ou des dilatations (lagrangien)
B : tenseur de Cauchy-Green gauche (eulérien)
Allongement et glissement
Comme en HPP les variations de produit scalaire permettent de calculer les variations de longueur et les variations d'angle.
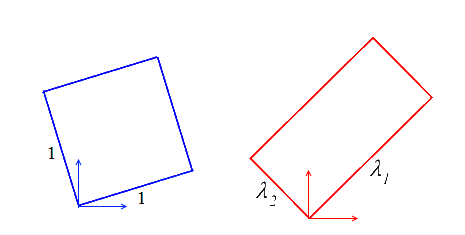
L'extension λ(N) dans la direction (lagrangienne; tout est bleu ici, je ne colorie plus !) N est définie comme le rapport
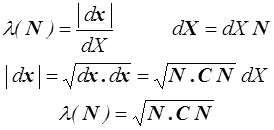
De même le glissement γ(M,N) dans deux directions (lagrangiennes) M et N initialement perpendiculaires est donné par
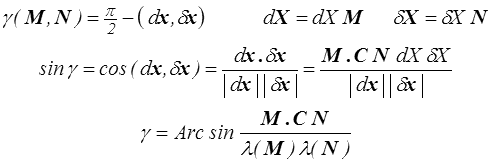
Les formules sont moins simples qu'en HPP (<) , (<) , mais la connaissance du tenseur des dilatations C (ou des déformations de Green-Lagrange E) permettent encore de caractériser allongement et glissement. On en tire en particulier la signification et une mesure possible des composantes de C. Il vient en effet
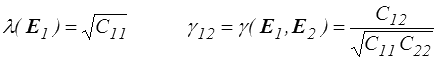
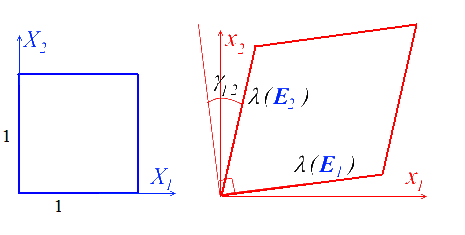
C'est une technique de mesure classiquement utilisée en disposant par exemple, avant déformation, une grille sur le matériau.
En particulier, et comme en HPP (<) , les directions principales de C correspondent aux directions qui après déformation restent perpendiculaires, et on notera λ1 et λ2 les extensions principales (Par rapport aux petites déformations on rappelle qu'il n'est plus nécessaire d'exagérer les déformations).
Ce que nous venons de faire avec C ou E peut également se faire à partir des tenseurs eulériens B ou A pour définir les variations de longueur et d'angle à partir des vecteurs eulériens dx, mais d'un point de vue pratique cela ne nous apporterait rien car il est contre nature et techniquement peu pertinent de « matérialiser » des vecteurs eulériens.
Décomposition polaire
Une autre approche se base sur le
Théorème de décomposition polaire.
On peut décomposer de manière unique le tenseur F (det F > 0 ) en
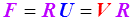
où R est une rotation R RT = RTR = 1
et où U et V sont deux tenseurs symétriques et définis positifs.
C'est un résultat d'algèbre linéaire tout à fait général mais apparemment peu utilisé en dehors de la MMC.
Pour démontrer ce théorème, on calcule
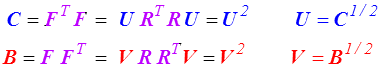
Les tenseurs U et V sont les racines carrées des tenseurs C et B que nous avons déjà rencontrés. Pour les calculer, il faut diagonaliser B et C et prendre dans le repère principal les racines des valeurs principales (<) . On calcule ensuite R par
R = F U −1 ou V −1F
et on vérifie directement que c'est bien une rotation.
Ce théorème permet de décomposer la transformation en une rotation et une déformation pure
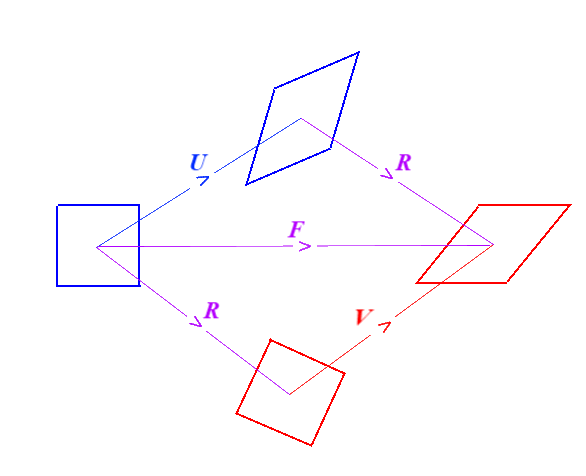
R tenseur de rotation (ou rotation propre)
U tenseur de déformation pure droit
C tenseur de Cauchy-Green droit
V tenseur de déformation pure gauche
B tenseur de Cauchy-Green gauche
Les tenseurs U et C sont lagrangiens, les tenseurs B et V sont eulériens, tandis que R est un tenseur mixte mi-eulérien mi-lagrangien.
La transformation F correspond
- à une déformation pure U dans Co suivie d'une rotation R de Co vers C (F = RU)
- ou bien à la rotation R de Co vers C suivie d'une déformation pure V dans C.
On obtient aussi
Cette décomposition est encore plus parlante si on représente la transformation dans les repères principaux de B et C
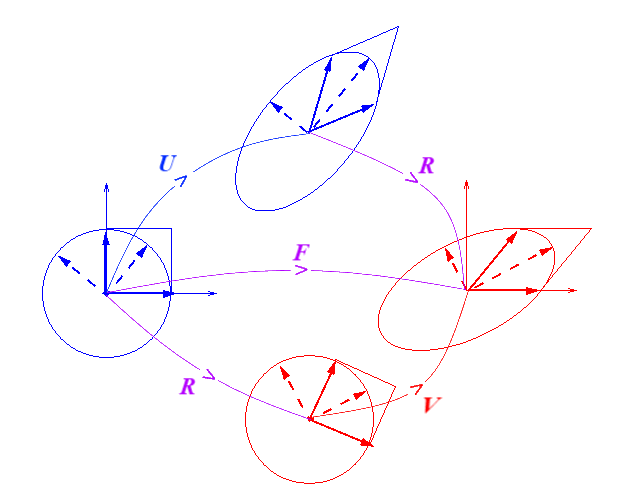
Le Cas bidimensionnel ===>
Outre ses applications importantes, le cas bidimensionnel permet des représentations géométriques parlantes et nous l'avons d'ailleurs largement utilisé. Nous vous proposons dans ce cadre, comme nous l'avions fait en HPP, une animation permettant de visualiser l'évolution des transformations (allongements, glissements et rotations) ainsi que la décomposition polaire. Il est important de souligner que les transformations peuvent maintenant être représentées en grandeurs réelles et sans amplification.
On peut aussi dans ce cas bidimensionnel aller beaucoup plus loin et généraliser le cercle de Mohr en un cercloïde de Mohr.
Les mesures de Seth-Hill
Nous avons pour l'instant introduit deux tenseurs de déformation (Green en lagrangien, Almansi en eulérien), mais on peut en définir bien d'autres. En fait, les tenseurs de déformation pure U ou V ou bien les tenseurs de Cauchy-Green C ou B contiennent essentiellement la même information, mais on peut choisir différentes manières pour la représenter (on parle de mesure de déformations).
Par exemple dans l'essai de traction on mesure la variation relative de longueur et on définit classiquement l'allongement par
Or ce sont les tenseurs U et V qui mesurent cet allongement. Ceci conduit naturellement à introduire deux nouvelles mesures
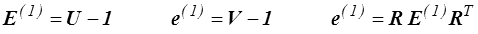
Plus généralement on peut définir si m est un nombre non nul
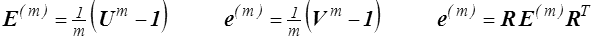
Pour élever le tenseur symétrique à la puissance m il suffit, si m est entier, de le multiplier m fois par lui-même. Si par contre m n'est pas entier, il faut alors revenir à la définition générale d'une fonction tensorielle (<) pour un tenseur symétrique.
Pour combler la lacune m = 0, on rajoute à la famille
Ces deux derniers tenseurs joueront un rôle important dans la suite et nous y reviendrons très bientôt, mais je me limite pour l'instant à les introduire pour compléter la liste de ces mesures dites de Seth-Hill.
Petites déformations
En petites perturbations on a écrit (<)
Les tenseurs de Cauchy-Green se calculent alors simplement
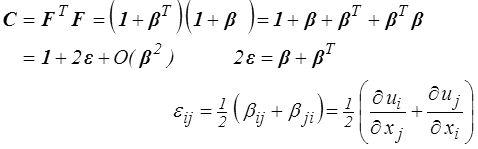
et on retrouve au premier ordre le tenseur des déformations infinitésimales ε (<) . Nous réservons désormais (comme nous l'avons déjà précédemment fait pour σ) la notation ε à cet usage.
Le tenseur des déformations de Green-Lagrange est alors
Remarquons que l'on peut écrire de manière générale en conservant le terme négligé et à condition d'utiliser le même repère dans C et Co
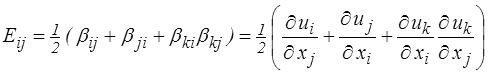
qui rajoute simplement à la formule usuelle un terme quadratique. On peut espérer, en rajoutant ce terme correctif non linéaire à la déformation, traiter des déformations non infinitésimales à peu de frais (mais à grand risque, aussi je vous déconseille ce genre d'acrobatie ; nous verrons plus loin à maintes reprises, que l'utilisation de ces tenseurs mérite plus de respect.) Si, sans être infinitésimales, les déformations restent petites cela peut marcher, mais prudence ! Cela reste néanmoins une pratique courante.
Le tenseur B se calcule de la même manière
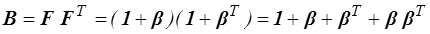
soit au premier encore
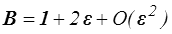
D'où pour B −1 et le tenseur d'Almansi
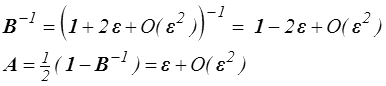
Pour les déformations pures U et V
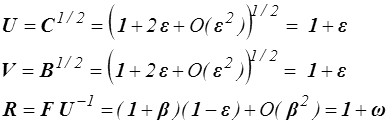
où ω est la partie antisymétrique du gradient du déplacement (<).
Quant aux mesures de Seth-Hill elles ont justement été construites pour que
En HPP tous les tenseurs de déformation coïncident au premier ordre pour redonner le tenseur des déformations infinitésimales que nous avions alors introduit (<) .
Le tenseur de Hencky
Nous avons déjà introduit les tenseurs de déformation logarithmique en tant que mesures de Seth-Hill pour m = 0. Ces tenseurs sont aussi appelés tenseurs de Hencky et nous les noterons H et h
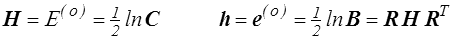
Leur manipulation est simple si on connaît les directions principales − il suffit alors de prendre le logarithme des valeurs principales − mais elle est beaucoup plus lourde dans le cas général. Par exemple, pour calculer B en fonction de h (ou C en fonction de H) on peut partir du développement en série
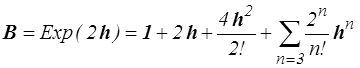
Pour calculer la différentielle de B il faut alors écrire
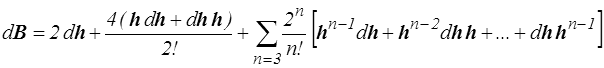
la différentielle dB est une fonction de h et dh. On peut écrire formellement
mais ce tenseur du quatrième ordre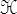 
n'a pas d'expression simple.
Si h et dh commutent alors on peut par exemple écrire
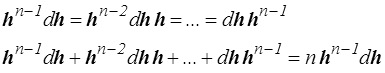
et en reportant dans le développement
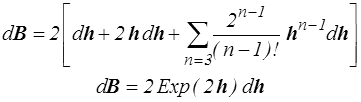
relation que l'on aurait pu être tenté d'écrire dès le départ
mais cela n'est en général par vrai (<) .
Ces tenseurs de Hencky semblent donc bien compliqués ! Et pourtant ils joueront un rôle essentiel dans la suite. Une des raisons pour cela est le fait qu'ils expriment très simplement la décomposition en dilatation sphérique et distorsion (<) . Nous avions alors posé
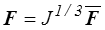
dont il découle, avec des notations évidentes,
mais qui ne se transpose pas simplement pour les déformations. Seules les déformations logarithmiques permettent d'écrire simplement
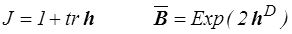
où hD est le déviateur du tenseur h.
On notera que la déformation logarithmique est également utilisée comme mesure de la déformation pour la courbe rationnelle de traction (<) .
Un premier exemple ===>
Nous savons maintenant décrire les contraintes et les déformations. La loi de comportement relie contraintes et déformations. Oui, mais lesquelles ? Nous y reviendrons bientôt, mais il est instructif, pour préparer le terrain, de se pencher sur un objectif plus modeste : peut-on généraliser simplement la loi de Hooke aux grandes transformations ?
Objectif modeste, certes, mais beaucoup plus subtil qu'il n'y paraît. Quitte à gâcher la surprise, la réponse finale sera oui ! mais à condition d'utiliser justement les déformations logarithmiques.