Loi de Hooke
Coefficients de Lamé
Nous nous limitons désormais au cas isotrope, c'est-à-dire, en termes simples, au cas où le matériau a les mêmes propriétés dans toutes les directions. Pour aller plus loin il faudrait donner à cette affirmation une traduction mathématique précise. Nous le ferons dans le cours de Comportement des Matériaux, lorsque nous introduirons l'anisotropie. Nous démontrerons alors que la loi élastique se réduit à une forme beaucoup plus simple
σij = λ εkk δij + 2 μ εij
Nous accepterons ce résultat dont la démonstration dépasse largement le cadre de ce cours. C'est la loi de Hooke (élasticité linéaire isotrope) avec deux constantes élastiques λ et μ appelées constantes de Lamé. Ces deux constantes sont homogènes à une contrainte et s'exprimeront en Pa (plutôt MPa, ou GPa d'ailleurs). Passant aux composantes on peut aussi écrire
σ11 = (λ + 2 μ) ε11 + λ ε22 + λ ε33
σ12 = 2 μ ε12 etc...
ou sous forme matricielle
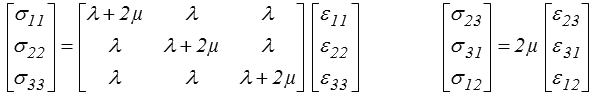
On remarquera que l'écriture trop simpliste σij = E εij correspond au cas λ = 0 avec E = 2 μ.
Sollicitations élémentaires
Pour illustrer cette loi de comportement, nous allons considérer trois sollicitations élémentaires.
En dilatation ou contraction isotrope (<)
ui = α xi εij = α δij
il vient directement (si le lecteur ne trouve pas cela si direct, nous l'invitons à expliciter l'une ou l'autre des trois formulations, indicielle, en composantes ou matricielle ; la dernière forme matricielle est certainement la plus commode)
σij = σ δij σ = (3 λ + 2 μ) α = 3 K α
le coefficient 3 K = 3 λ + 2 μ est appelé module de compressibilité (bulk modulus, en anglais, il est alors souvent noté B ).
En glissement simple (<) on obtient, encore plus simplement,
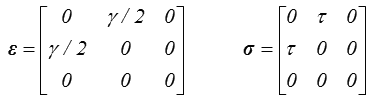
avec
τ = G γ = μ γ
où le coefficient G est appelé module de cisaillement ou module de Coulomb. Bien évidemment, c'est aussi la constante de Lamé μ ; l'utilisation de l'une ou l'autre de ces deux notations est assez typée et traditionnelle et il convient, pour l'instant, de bien conserver à l'esprit les deux notations G et μ, et de savoir passer de l'une à l'autre en fonction de son interlocuteur.
La traction simple est moins directe puisque l'on part ici du tenseur des contraintes
σ11 = σ σ22 = σ33 = σ12 = σ23 = σ31 = 0
et qu'il faut donc inverser la loi de comportement. Le plus direct est de partir de l'écriture en composantes, qui donne directement
ε12 = ε23 = ε31 = 0
σ = (λ + 2 μ) ε11 + λ ε22 + λ ε33
0 = λ ε11 + (λ + 2 μ) ε22 + λ ε33
0 = λ ε11 + λ ε22 + (λ + 2 μ) ε33
système de 3 équations à 3 inconnues qui donne, par exemple, ε22, ε33 et σ en fonction de ε11 = ε
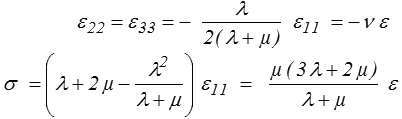
où les deux coefficients
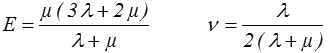
sont respectivement appelés module d'Young (E, homogène à une contrainte, donc en MPa ou GPa) et coefficient de Poisson (ν, sans dimension).
Inversion de la loi de comportement
L'écriture inverse, donnant les déformations en fonction des contraintes, peut s'obtenir de différentes manières. On remarque d'abord que cette inversion est directe pour les composantes non diagonales
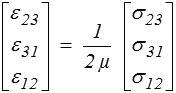
alors que, pour les composantes diagonales, il faut inverser une matrice 3x3. On préfère alors partir des résultats obtenus plus haut en traction, en superposant les déformations induites par chacune des trois composantes σ11, σ22, σ33. On obtient ainsi pour ε11
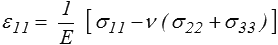
Une contrainte σ22 seule engendrera une contraction ε11 = − ν ε22 = − ν σ22 / E. On obtient ainsi
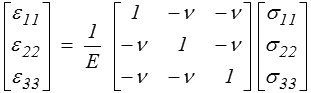
soit, en revenant aux notations tensorielles,
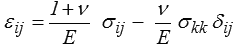
Une autre méthode instructive, pour réaliser cette inversion, est de partir de la forme initiale de la loi de Hooke
σij = λ εkk δij + 2 μ εij
et d'en prendre la trace. On obtient ainsi
σii = (3 λ + 2 μ) εii
qui donne εkk en fonction de σkk
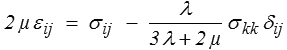
Nous laissons au lecteur méfiant le soin de vérifier que, compte tenu des expressions obtenues plus haut pour E et ν, cette forme coïncide bien avec celle que nous avons trouvée ci-dessus.
Dilatation sphérique et distorsion
Une nouvelle écriture, la plus porteuse de sens sans doute, s'obtient en décomposant contraintes et déformations en partie sphérique et déviateur ((<), (<))

Partant toujours de la loi initiale, on obtient directement, en prenant la trace et le déviateur,
σI = 3 K εI 3 K = 3 λ + 2 μ
sij = 2 G eij 2 G = 2 μ
Ceci montre au passage l'importance théorique des deux essais de contraction isotrope et de glissement simple, qui permettent justement de caractériser expérimentalement ces deux comportements, alors que l'essai de traction, qui les combine, est plus facile à réaliser mais plus délicat à analyser.
La loi élastique revient en fait à deux lois scalaires, portant respectivement sur les parties sphériques et les déviateurs. Si les deux coefficients sont identiques (3 K = 2 G, λ = 0), on obtient une simple loi de proportionnalité σij = 2 μ εij, mais ces deux coefficients seront en général différents, ce qui correspond au fait que la matière réagit différemment aux sollicitations isotropes (c'est-à-dire, pour faire simple, aux contraintes normales) et aux sollicitations déviatoires (c'est-à-dire, toujours pour faire simple, aux contraintes de cisaillement).
Ce découplage est en fait une caractéristique générale du comportement isotrope, et il découle en réalité d'un résultat mathématique général sur les opérateurs linéaires isotropes.
Constantes élastiques
L'essentiel est le fait qu'une loi élastique isotrope fait intervenir deux constantes indépendantes, par exemple
- le module d'Young E,
- le coefficient de Poisson ν.
Ces deux constantes, directement accessibles dans un essai de traction, donc relativement faciles à mesurer, sont les plus courantes.
Le module d'Young, homogène à une contrainte, caractérise la rigidité du matériau ; quelques valeurs typiques sont
E = 210 x 10 9 Pa pour l'acier,
80 x 10 9 Pa pour les alliages d'aluminium.
Le coefficient de Poisson caractérise la contraction transversale dans un essai de traction. Pour un matériau incompressible tr ε = 0 et ν = 1/2, ce qui est presque le cas pour les polymères. Le cas ν = 0 correspond à un matériau qui, en traction, s'allonge sans contraction transversale, c'est à peu près ce qui se passe pour les matériaux de type mousse, et on considère traditionnellement que le coefficient de Poisson est compris entre ces deux extrêmes.
0 ≤ ν ≤ 1/2
Une valeur typique des matériaux métalliques est ν = 0.3. Il faut toutefois remarquer que, d'un point de vue théorique, rien ne s'oppose à un coefficient de Poisson négatif, c'est-à-dire à un matériau qui se dilate latéralement lorsqu'on l'allonge. Nous verrons plus loin que les bornes théoriques sont
−1 ≤ ν ≤ 1/2
En fonction du problème traité, d'autres couples de constantes pourront s'avérer plus commodes, par exemple
- les deux coefficients de Lamé λ et μ,
- les deux modules K et G de dilatation et de cisaillement,
et on peut, bien évidemment, passer de l'un à l'autre. On a, par exemple,
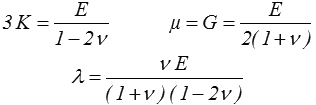
Signalons, pour terminer, l'écriture suivante
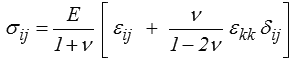
expression des contraintes en fonction des déformations lorsque l'on connaît E et ν.
Energie élastique
Dans le cas linéaire, l'énergie élastique est donnée par
w = ½ σij εij
soit, en fonction des déformations,
w = ½ λ εii εkk + μ εij εij
ou, en fonction des contraintes,
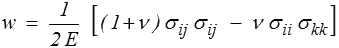
Si l'on utilise la décomposition en partie sphérique et déviateur
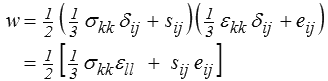
et, en utilisant les relations obtenues plus haut,
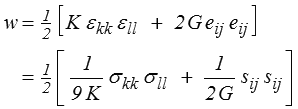
que l'on peut interpréter comme la somme de deux contributions provenant de la compressibilité et du cisaillement respectivement.
Dans la mesure où dilatation sphérique et déviateur sont indépendants, une condition nécessaire et suffisante pour que l'énergie soit définie positive, ce que l'on interprète habituellement comme condition de stabilité élastique, est que
K ≥ 0 G ≥ 0
Compte tenu des expressions obtenues plus haut pour K et G en fonction de E et ν, ceci donne, comme annoncé plus haut,
E ≥ 0 −1 ≤ ν ≤ 1/2
Elasticité plane
La loi de Hooke est, par essence, tridimensionnelle. Dans son application à des problèmes bidimensionnels, il faudra distinguer déformations planes et contraintes planes.
Une situation de déformation plane est définie par
u1 = u1 ( x1 , x2 ) u2 = u2 ( x1 , x2 ) u3 = 0
de sorte que ε13 = ε23 = ε33 = 0. La loi de Hooke s'écrira alors simplement
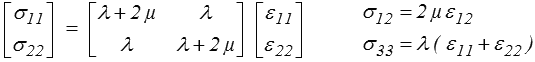
Si par contre on veut exprimer les déformations en fonction des contraintes, il faut prendre en compte le fait que la contrainte σ33 n'est pas nulle. La loi complète (<) donne alors
E ε33 = σ33 − ν ( σ11 + σ22 ) = 0 σ33 = ν ( σ11 + σ22 )
soit, en reportant cette valeur dans l'expression de ε11 et ε22,
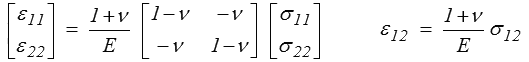
L'énergie de déformation s'écrit de même
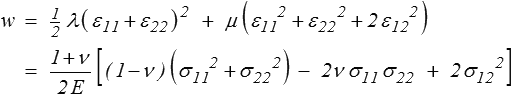
Cette description est valable pour une pièce très épaisse ; il faut, dans le cas d'une plaque mince, la remplacer par une approximation de contraintes planes
σ13 = σ23 = σ33 = 0
La loi de Hooke est alors simplement
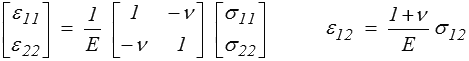
mais, dans l'autre sens, la déformation ε33 n'est pas nulle − elle décrit en fait la variation d'épaisseur de la plaque −. Le plus simple est alors d'inverser la loi précédente pour obtenir
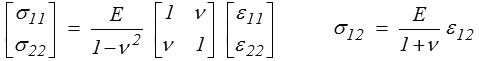
avec les expressions correspondantes pour l'énergie.
Rappelons qu'en élasticité linéaire
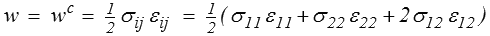
et dans la pratique il sera en général plus commode de calculer l'énergie à partir de la loi de comportement plutôt qu'à partir de la forme quadratique.
