Le modèle de Kelvin-Voigt
Définition
Le modèle de Kelvin ou Kelvin-Voigt correspond au montage parallèle d'un ressort et d'un amortisseur
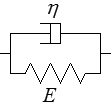
Sa loi de comportement s'obtient directement en combinant les règles de montage parallèle et les lois élémentaires du ressort et de l'amortisseur
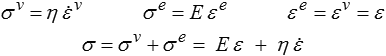
en notant v comme visqueux [resp. e comme élastique] ce qui est relatif à l'amortisseur [resp. au ressort].
Comportement en fluage
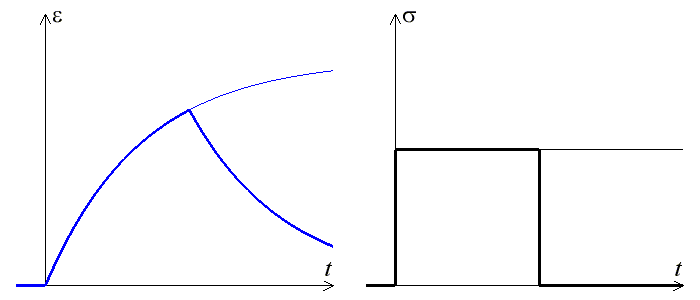Si on impose à l'instant t une contrainte σo constante, la réponse ε(t) s'obtiendra par intégration de l'équation différentielle
σo = E ε + η 
équation différentielle qui, avec la condition initiale ε(0) = 0, s'intègre directement pour donner
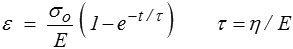
où la constante τ = η / E, homogène à un temps, est le « temps de fluage » ou « de retard ».
Au départ la contrainte est entièrement supportée par l'amortisseur, mais sous l'effet de cette contrainte il s'allonge en entraînant le ressort qui, en s'allongeant, va prendre à son compte une part de plus en plus grande de la contrainte appliquée, jusqu'à en assumer finalement la totalité. Plus précisément
si t 
∞ ε ~ σo / E
si t 0 ~ σo / η
Le modèle de Kelvin se comporte somme un amortisseur aux temps courts (comportement instantané) et comme un ressort aux temps longs (comportement différé).
Si à l'instant to on relâche la contrainte appliquée (courbe en trait gras), alors un calcul simple montre de même
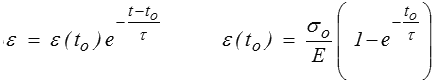
Le matériau retrouve progressivement sa forme initiale (recouvrance différée).
Comportement en relaxation
L'essai de relaxation stricto-sensu est impossible (de par la présence du terme en qui interdit toute déformation instantanée). Mais il n'est pas non plus réalisable technologiquement. Si on déforme rapidement le matériau jusqu'à εo, pour ensuite le maintenir constant, alors la contrainte, très grande pendant la montée en déformation, se stabilise à la valeur E εo sitôt que l'on fixe la déformation.
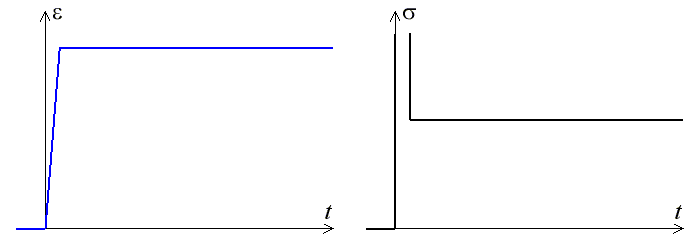Le modèle de Kelvin-Voigt ne présente pas d'effet de relaxation (diminution de la contrainte nécessaire pour maintenir une déformation constante).