Viscoélasticité linéaire
Les modèles viscoélastiques (<), constitués de ressorts et d'amortisseurs, sont linéaires et c'est cette propriété de linéarité qui caractérise le comportement viscoélastique et conduit donc à la viscoélasticité linéaire.
Principe de superposition de Boltzmann
Pour un modèle de comportement cette propriété de linéarité correspond à la linéarité de la fonctionnelle de réponse (<): la réponse à la somme (ou plus généralement une combinaison linéaire) de sollicitations est la somme des réponses à chaque sollicitation.
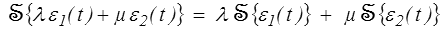
ou bien
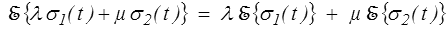
Considérons par exemple un essai à vitesse de déformation constante
ε = 
o t
ou plus exactement
ε = o t 
(t) ( o t si t ≥ 0 , 0 si t ≤ 0 )
où (t) est l'échelon unité (fonction de Heaviside, 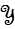(t) = 0 si t < 0, 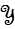(t) = 1 si t > 0). Nous supposerons en effet dans la suite que la sollicitation commence à l'instant t = 0, ε = σ = 0 pour t ≤0. Considérez donc que, sauf mention explicite du contraire, toutes les fonctions du temps sont nulles pour t < 0 et doivent donc être multipliées par un échelon unité que nous omettrons souvent dans la notation.
Il résulte de la linéarité que la réponse à cet essai est proportionnelle à o . On écrira
ε = o t σ = o L(t)
où L(t) est la réponse correspondant à une vitesse unité. Si maintenant on arrête la déformation à to, cette sollicitation est la superposition des deux essais vert et magenta, et la réponse en découle directement
σ = o L(t) − o L(t−to )
Plus généralement, la linéarité nous permettra de suivre la réponse à une sollicitation complexe à partir de quelques essais élémentaires.
Fonctions de fluage et de relaxation
L'essai de fluage (<) correspond à un échelon de contrainte
σ = σo (σo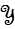 (t) en fait)
La réponse sera alors
ε = σo J(t)
où J(t), réponse en déformation à un essai de fluage pour une contrainte unité, est la fonction de fluage du matériau.
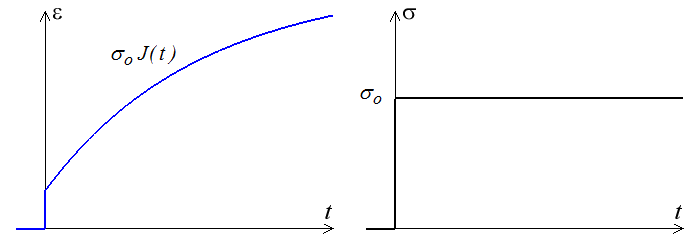
Suivant la démarche décrite plus haut, on peut en tirer directement la réponse à un créneau de contrainte
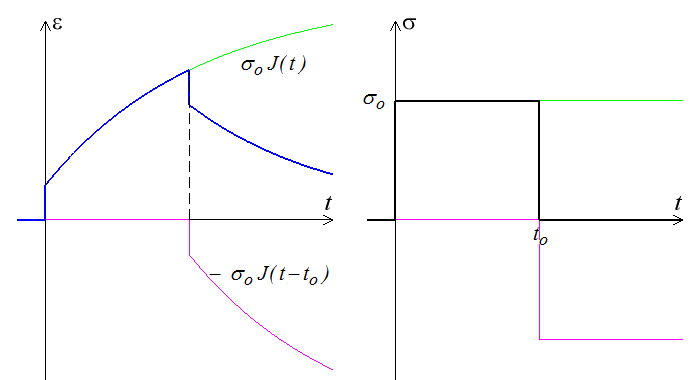
ou à une sollicitation en escalier
De même la fonction de relaxation E(t) est la réponse à un essai de relaxation pour une déformation unité
ε = εo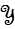 (t) σ = εo E(t)
On remarquera toutefois que cette fonction, définie sans difficulté pour un modèle avec élasticité instantanée (<), pose problème pour un modèle visqueux qui ne peut supporter une discontinuité de déformation et donc un essai de relaxation. Il faudra faire intervenir une fonction de Dirac.
Calcul de la réponse
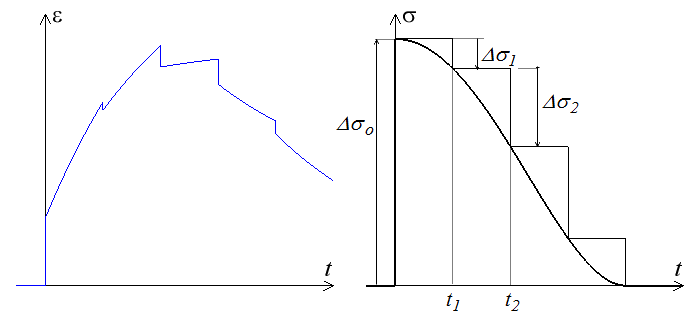
Connaissant la fonction de fluage, on pourra utiliser la superposition pour déterminer la réponse à une contrainte fonction en escalier.
σ = Δσo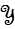 (t) + Δσ1 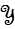(t−t1) + Δσ2 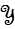(t−t2) + ...
ε = Δσo J (t) + Δσ1 J (t−t1) + Δσ2 J (t−t2) + ...
Les mathématiciens montrent que toute fonction peut être approchée par une fonction en escalier. Nous pouvons donc généraliser ce résultat à une sollicitation quelconque. La somme finie devient alors une intégrale
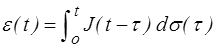
Dans cette écriture on remarquera que l'histoire de contrainte peut comporter des sauts dσ = Δσ et des évolutions continues, dσ(τ) =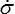 
(τ) dτ. C'est pour le mathématicien une intégrale de Stieltjes.
Ainsi la connaissance de la fonction de fluage permet d'écrire la loi de comportement générale, c'est -à-dire la fonctionnelle de réponse qui s'exprime ici explicitement sous forme d'une intégrale.
Ce résultat, essentiel, est en fait tout à fait classique et utilisé dans bien d'autres domaines, par exemple en automatique ou en électronique. C'est en fait la lecture rhéologique d'un résultat général en théorie des systèmes linéaires et souvent connu sous le nom de théorème de Duhamel. C'est aussi en mathématiques le théorème selon lequel toute forme linéaire peut être considérée comme un produit scalaire.
La viscoélasticité linéaire peut en fait être considérée comme une application de la théorie des systèmes et nous profiterons largement de ses acquis (c'est malheureusement le seul cas où on peut le faire).
Lois héréditaires de Volterra
La loi viscoélastique générale s'écrira donc sous forme d'une intégrale
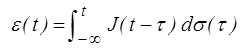
souvent appelée intégrale héréditaire de Volterra. On remarquera que l'on a, dans cette écriture, remplacé la borne inférieure t = 0 par t =−∞, ce qui est légitime puisque l'on a considéré que le matériau était au repos (ε = σ = 0) avant le début de la sollicitation que nous avons choisi comme origine des temps.
On trouve dans la littérature d'autres formes équivalentes. Par exemple une intégration par parties donne
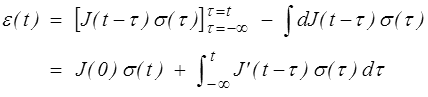
puisque σ(−∞) = 0 et en notant J' la dérivée de la fonction de fluage. Le changement de variable t−τ = s permet aussi d'écrire
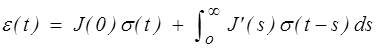
Par ailleurs, on peut obtenir, pour une sollicitation à déformation imposée, une formulation symétrique faisant intervenir, à la place de la fonction de fluage, la fonction de relaxation
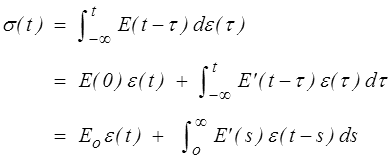
Transformée de Laplace-Carson ===>
Le lecteur un peu habitué à ces questions (classiques, répétons-le, en automatique et en électronique) aura reconnu dans cette loi intégrale un produit de convolution
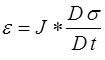
La déformation ε considérée comme une fonction du temps est le produit de convolution de la fonction de fluage par la dérivée Dσ / Dt (dérivée au sens des distributions, d'où la notation D / Dt plutôt que d / dt, mais pas d'affolement, c'est important pour la rigueur mathématique mais totalement indolore pour les applications).
Ceci conduit tout naturellement à l'utilisation de la transformation de Laplace − ou plus précisément de Laplace-Carson − associant à une fonction du temps f (t) sa transformée f *(p) définie par
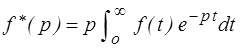
En transformée de Laplace-Carson la loi de comportement viscoélastique s'exprime par un simple produit
ε*(p) = J *(p) σ*(p) σ*(p) = E *(p) ε*(p)
où J *(p) et E *(p) sont les transformées de Laplace-Carson des fonctions de fluage et de relaxation. On parle souvent de module opérationnel. On en déduit en particulier que ces deux fonctions sont inverses lune de l'autre
E *(p) J *(p) = 1
L'utilisation de cette transformée de Laplace-Carson réduit (presque !) les calculs viscoélastiques à des simples calculs algébriques. Pour calculer la réponse ε(t) à une sollicitation σ(t) quelconque il suffit de
- Calculer la transformée σ*(p) de σ(t).
- En déduire ε *(p) = J *(p) σ*(p).
- Revenir à l'original ε(t).
C'est cette dernière étape qui peut poser problème (d'où le presque de mon affirmation). Dans la pratique on pourra souvent s'en sortir en utilisant le mini-formulaire (<) .