Viscoélasticité harmonique
Pour les applications, comme pour la caractérisation du comportement, il est souvent intéressant de considérer le comportement d'un matériau sous sollicitation harmonique ou plus généralement sous chargement cyclique ou périodique : la linéarité permet en effet de traiter tout chargement périodique par superposition de sollicitations harmoniques (série de Fourier). On parle aussi souvent − improprement − de viscoélasticité dynamique. En fait cela ne concerne pas les effets dynamiques qu'il faudra effectivement prendre en compte si les fréquences considérées sont du même ordre que les fréquences propres de la structure étudiée. Cela devient alors un problème de structure et non de matériau.
Viscoélasticimétrie
Si on impose au matériau une sollicitation harmonique (par exemple une déformation), la réponse sera également harmonique. C'est une propriété générale des systèmes linéaires et nous le démontrerons plus précisément plus loin. On écrira ainsi
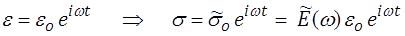
où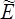 
(ω) est le module complexe (raideur complexe). On décompose traditionnellement ce module en partie réelle et partie imaginaire, ou bien en module et argument
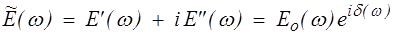
Les parties réelle et imaginaire E' et E" sont respectivement appelées module de conservation et module de perte.
On écrira par exemple
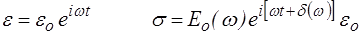
soit en fait (n'oubliez pas en utilisant ces notations complexes que ce n'est qu'un intermédiaire de calcul et que la réalité porte sur les parties réelle ou imaginaire)
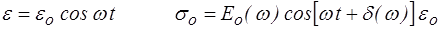
La réponse harmonique est caractérisée par le rapport des amplitudes Eo et un déphasage − ou angle de perte − δ.
Si l'on impose plutôt une contrainte harmonique, alors on obtiendra de même
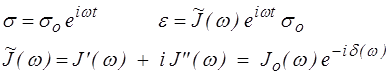
où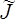 
(ω) = 1/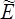(ω) est la complaisance complexe (évitez le mot compliance, du moins lorsque vous parlez en français: c'est le terme anglais).
La détermination expérimentale de ces modules complexes se fait sur des « viscoélasticimètres », appareils usuels dans les laboratoires. Le principe en est très simple. On impose par exemple une déformation harmonique, on mesure la contrainte et un traitement de signal classique permet d'en extraire rapport d'amplitude et déphasage.
Cette caractérisation s'accompagne en général d'un balayage en fréquence ou en température, (les deux étant en fait reliées, c'est l'équivalence temps-température).
Cette caractérisation viscoélasticimétrique est très commune car relativement simple à mettre en œuvre. Tellement simple d'ailleurs qu'on l'utilise parfois à tort et à travers : la notion de module complexe n'a de sens précis qu'en viscoélasticité linéaire. Sinon l'information expérimentale peut être intéressante, mais on ne peut plus l'interpréter aussi simplement.
Réponse harmonique
La détermination du module complexe à partir de la fonction de relaxation ou de fluage peut se faire en suivant la méthode générale décrite plus haut (<) . Pour une sollicitation harmonique
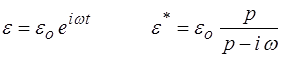
La réponse en contrainte est donc
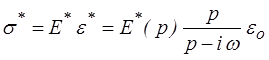
et il « suffit » de revenir à l'original σ(t). Or on a vu plus haut que E *(p) était (exactement ou éventuellement de manière approchée par discrétisation du spectre) une fraction rationnelle. On peut donc calculer l'original σ(t) par réduction de cette fraction rationnelle. Le calcul est un peu technique et peut être sauté sans dommage majeur. Il est néanmoins instructif et mérite d'être détaillé.
Le module opérationnel peut s'écrire
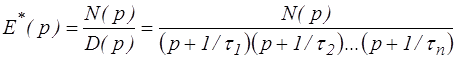
où le dénominateur D(p) a été explicité en fonction des temps de relaxation. On pourrait de même expliciter le numérateur N(p) en fonction des temps de fluage, mais ce n'est pas utile pour notre objectif actuel. En reportant dans l'expression de la contrainte
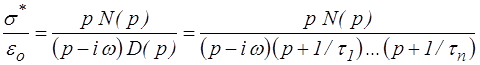
fraction que l'on décompose en éléments simples
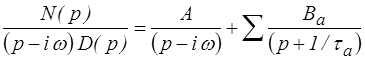
La technique de calcul des coefficients A et Ba est classique. Pour B1 par exemple, on multiplie par (p+1/τ1 )
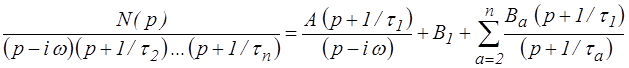
identité qui pour p = −1/τ1 donne directement
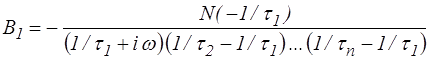
et de même pour B2 ... Bn . Pour A, on multiplie de même par (p − iω)
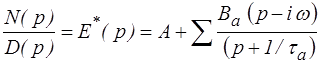
qui, pour p = iω donne directement A = E *(iω).
On obtient donc finalement
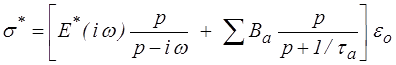
qui, d'après le mini-formulaire (<) , donne directement
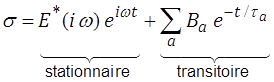
Le second terme décrit le régime transitoire résultant du démarrage de la sollicitation (nulle par hypothèse pour t < 0). Notre calcul correspond en fait à imposer
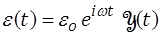
Ce terme transitoire est rapidement amorti.
Le premier terme est le régime stationnaire harmonique cherché et nous en tirons le module complexe
Modules complexes
Il est maintenant facile, compte tenu des résultats obtenus précédemment, de déterminer le module complexe des modèles série et parallèle généralisés.
Pour le module série par exemple
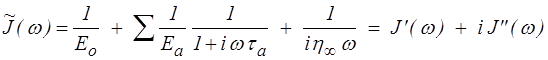
d'où l'on extrait facilement les parties réelle et imaginaire
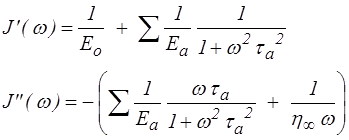
De manière similaire on obtient pour le modèle parallèle généralisé (<)
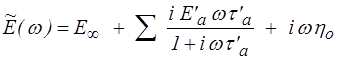
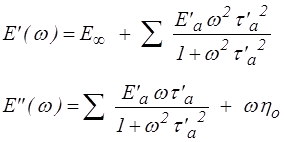
Considérons, pour fixer les idées, le cas d'un solide avec élasticité instantanée (les deux amortisseurs ηo et η∞ sont absents)
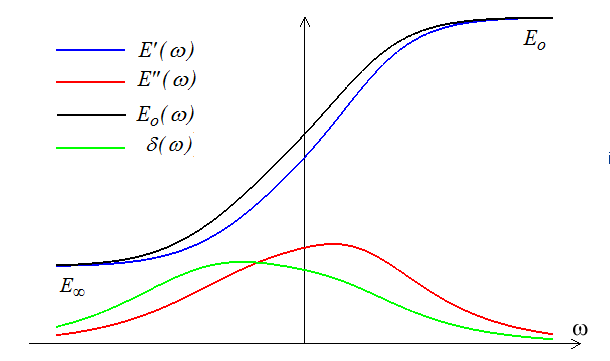
Les courbes ci-dessus décrivent l'évolution en fonction de la fréquence (échelle logarithmique en général) des deux modules réel et imaginaire ou si l'on préfère du rapport d'amplitude et de l'angle de perte.
Ces résultats s'étendent sans difficulté majeure au cas d'un spectre continu, les sommes finies étant simplement remplacées par des intégrales. La modélisation d'un matériau viscoélastique se fera souvent à partir des courbes obtenues expérimentalement par viscoélasticimétrie. Le nombre de variables internes nécessaires (c'est-à-dire d'éléments dans le modèle rhéologique discret) dépend bien évidemment de la précision souhaitée et de l'étendue de la plage de fréquence. On dit assez souvent qu'il faut un modèle intermédiaire par décade de fréquence.
Diagramme de Cole-Cole
Une manière commode de représenter les résultats est de tracer dans le plan complexe l'évolution du module complexe 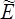(ω) en fonction de ω. C'est la représentation de Cole-Cole classique en électronique et en automatique.
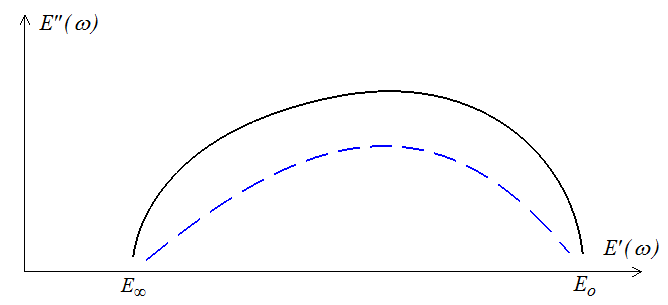
On a tracé ci-dessus l'allure de ce diagramme (toujours pour un solide avec élasticité instantanée). C'est un demi-cercle pour le modèle de Poynting, une courbe plus complexe dans le cas général, mais on montre que pour un modèle rhéologique discret cette courbe rejoint l'axe réel (en Eo aux hautes fréquences, ω → ∞ et en E∞ aux basses fréquences, ω → 0) avec une tangente verticale (courbe noire).
Les courbes obtenues expérimentalement ressemblent en général davantage à la courbe pointillée bleue, ce qui suggére qu'elles arrivent sur l'axe réel avec un angle non droit, en contradiction avec ce que nous venons de voir. Pour lever cette difficulté on peut introduire des modèles paraboliques caractérisés par une fonction de relaxation du type
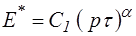
où α est un paramètre réel compris entre 0 et 1. Ce sont en fait des modèles intermédiaires entre le ressort (α = 0) et l'amortisseur (α = 1). Les calculs théoriques sont plus lourds et font appel à la notion de dérivée fractionnaire. C'est souvent une alternative commode et économique car elle permet de décrire avec peu d'éléments (le modèle standard biparabolique représenté ci-dessous en fait intervenir deux, liés aux deux angles d'arrivée sur l'axe réel) ce qui exigerait dans les représentations série ou parallèle généralisées, toujours possibles, un très grand nombre d'éléments.
