Transformation de Laplace-Carson
Définition et propriétés
Partant d'une fonction f (t) définie pour tout t > 0 (et par convention supposée nulle pour t < 0), on définit sa transformée de Laplace-Carson par

On notera, par rapport à la transformation de Laplace classique, la présence du facteur p avant l'intégrale. Sa raison d'être apparaîtra plus loin.
Une propriété essentielle de cette transformation est le fait que la dérivée par rapport au temps y devient une simple multiplication par p
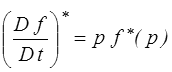
substituant ainsi au calcul différentiel un simple calcul algébrique, c'est ce que l'on appelle le « calcul opérationnel » utilisé avec succès dans de nombreuses applications.
On remarquera dans notre écriture la notation D / Dt, symbole d'une dérivation au sens des distributions, et l'absence de la valeur de la fonction à l'origine. On trouve en effet dans les formulaires standard la formule
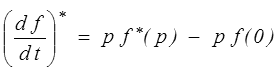
mais la présence de ce terme f (0) correspond à la discontinuité à l'origine de la fonction f, nulle pour t < 0 par convention, et donc non dérivable au sens strict. La théorie des distributions est l'outil mathématique adapté. On retiendra simplement que la théorie des distributions justifie mathématiquement nos calculs en prenant en compte, de manière transparente pour l'utilisateur, les discontinuités.
Produit de convolution
Pour les applications, l'intérêt majeur de la transformée de Laplace − comme d'ailleurs sa cousine la transformée de Fourier− est de transformer en opérations algébriques simples des opérations plus complexes pour les fonctions originales. Ainsi la dérivation devient un simple produit par p. C'est aussi le cas du produit de convolution : la transformée de Laplace (usuelle) du produit de convolution de deux fonctions est le produit de leurs transformées de Laplace. Toutefois notre loi de comportement viscoélastique (<) fait intervenir une dérivée. C'est la raison pour laquelle on utilise, plutôt que la transformée de Laplace classique, la transformée de Laplace-Carson obtenue en multipliant par p la transformée de Laplace classique. On obtient alors directement
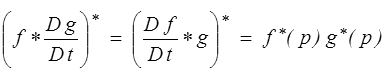
de sorte que notre loi de comportement viscoélastique devient simplement
σ*(p) = E *(p) ε*(p) ε*(p) = J *(p) σ*(p)
Mini-formulaire
La transformée de Laplace présente toutefois, par rapport à la transformée de Fourier, un inconvénient majeur : la transformée inverse n'est pas simple, et la détermination d'une fonction f (t) à partir de sa transformée de Laplace-Carson f *(p) (retour à l'original) est en général une opération mathématique difficile. Elle sera par contre simple si l'on peut se ramener à des transformées connues. Il est donc important de disposer d'un formulaire. On utilisera avec profit le formulaire ci-dessous.
original transformée
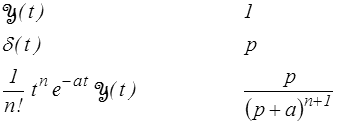
On remarquera dans la dernière formule la présence nécessaire de la fonction de Heaviside : ceci rappelle que la transformée de Laplace-Carson s'applique uniquement à des fonctions f(t) définies pour t > 0 et supposées nulles pour t < 0. Elle sera en général non écrite car sous-entendue. On écrit donc par application de la dernière formule

ce qui, en viscoélasticité nous suffira le plus souvent, car on trouvera en général nos transformées sous forme de fractions rationnelles. La décomposition en éléments simples de cette fraction rationnelle permettra alors de revenir à l'original par application de ces transformées élémentaires. On trouve ainsi
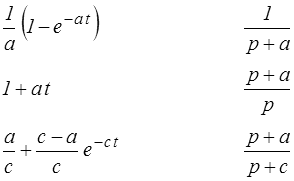
La dernière formule par exemple s'obtient simplement en réduisant la fraction
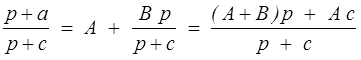
qui, par identification, donne A et B
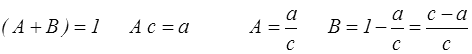
d'où l'original
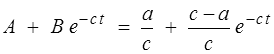
Enfin on remarque que les comportements asymptotiques pour t → 0 et t → ∞, dont on verra plus loin la signification, s'obtiennent à partir de ceux pour p → ∞ et p → 0 respectivement:
t → ∞  p → 0
p → 0
t → 0  p → ∞
p → ∞
