Lois de comportement
Problèmes de MMC
Pour un problème statique ou quasi-statique (<) et dans le cadre des petites perturbations, un problème de MMC revient à calculer le champ de contrainte σij( x) et le champ de déplacement ui(x), vérifiant
- les équations d'équilibre
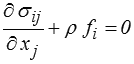
- les conditions aux limites statiques ou cinématiques,
- la loi de comportement.
C'est à cette dernière composante que nous nous intéressons ici. C'est par elle que l'on prendra en compte la nature physique des matériaux et elle se traduira finalement par une relation entre le tenseur des contraintes et le tenseur des déformations.
La résolution d'un problème de structure exige, pour relier les efforts appliqués (forces de volume f et forces surfaciques T ) aux déplacements u, de passer par les contraintes et les déformations qui en résultent à l'échelle du matériau.
En règle générale cette résolution sera réalisée numériquement et le plus souvent par un calcul éléments finis. Il convient donc de conserver présent à l'esprit que toutes les lois de comportement que nous développerons dans la suite de ce cours ont vocation à être intégrées dans un tel code de calcul. Nous n'évoquerons que rarement cet aspect, mais il est important.
Energie et dissipation
Les échanges d'énergie joueront, dans la caractérisation du matériau, un rôle essentiel. En négligeant les couplages thermomécaniques, le bilan énergétique fondamental (<) est
σij 
ij = 
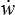+ ø ø ≥ 0
La puissance mécanique fournie au système (pour le déformer ; rappelons qu'une partie sera transformée en énergie cinétique) est en partie stockée sous forme d'énergie et en partie dissipée, c'est-à-dire dégradée sous forme de chaleur.
C'est ainsi, par exemple, que nous avons construit le modèle élastique linéaire
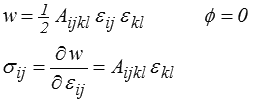
et, dans le cas isotrope, la loi de Hooke
w = ½ λ εkk εjj + μ εij εij
σij = λ εkk δij + 2 μ εij
En mécanique des fluides
Il peut sembler (et il est effectivement) incongru de parler de mécanique des fluides dans un cours de mécanique des matériaux solides et limité aux petites perturbations, et pourtant...!
Les matériaux réels peuvent, suivant leur nature et les circonstances, présenter certains aspects de comportement fluide, et nous devons intégrer cette composante dans notre panorama. En fait, la Mécanique des Matériaux, au sens où nous l'entendons ici, commence sitôt que nous quittons la mécanique des solides élastiques et la mécanique des fluides classique. Un cours de Mécanique des Matériaux exigerait donc en principe de quitter le cadre des petites perturbations. Si, comme on le fait souvent, nous avons néanmoins choisi de nous limiter ici au cas des petites perturbations, c'est essentiellement pour une raison technique. Nous y reviendrons plus loin (>).
Les modèles de la Mécanique des Fluides Classique (<) (fluide parfait et fluide visqueux, compressibles ou incompressibles) font donc partie, au moins comme cas limite, de l'univers que nous nous proposons d'explorer. De plus ils vont nous fournir une illustration flagrante de l'importance du bilan énergétique fondamental.
Le bilan énergétique s'écrit dans ce cadre
σij Dij = ρ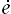 
+ ø
L'énergie dans un fluide ne dépend que de la masse volumique. La dissipation peut alors s'écrire (<)
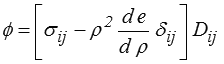
On en tire pour un fluide parfait (<) , c'est-à-dire non dissipatif (ø = 0),
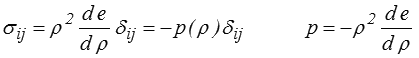
et pour un fluide visqueux newtonien (<) − c'est en fait un premier exemple d'application des relations d'Onsager (>).
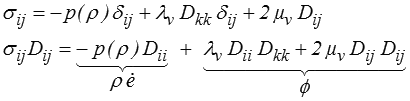
C'est donc un premier exemple d'une partition de la puissance mécanique fournie entre énergie et dissipation. Cette partition jouera un rôle essentiel dans la suite.
Dans le cas incompressible, ρ = ρo, donc e = eo, il n'y a donc pas d'énergie stockée, et Dii = div V = 0. La dissipation devient donc
ø = σij Dij Dii = 0
qui conduit au fluide parfait incompressible (<) si ø = 0 (c'est, avec le solide rigide, le seul modèle qui ne donne lieu à aucun échange d'énergie), et dans le cas dissipatif au fluide visqueux newtonien incompressible (<)
σij = − p δij + 2 μ Dij
qui dissipe de l'énergie sans en stocker.
Il est remarquable que les 4 modèles de la mécanique des fluides classique illustrent les 4 variantes possibles du bilan d'énergie : avec ou sans énergie stockée, avec ou sans dissipation.
Terminons cette excursion en Mécanique des Fluides, finalement beaucoup plus raisonnable qu'il n'y paraissait au départ, en rassurant le lecteur : malgré ce qui a été dit plus haut, la Mécanique des Matériaux en petites perturbations recouvre malgré tout un très grand nombre d'applications. Le passage aux grandes transformations ne sera pas toujours indispensable.
Loi de comportement générale
La loi de comportement donne une relation entre contraintes et déformations, et effectivement la loi élastique donne σij en fonction de εij ou vice-versa. Il s'agit là toutefois d'un cas très particulier . En général pour connaître la contrainte à l'instant t il ne suffira pas de connaître la déformation à l'instant t : il faut en fait également connaître toute l'histoire de déformation, c'est-à-dire la manière dont on est arrivé à cette déformation.
Un premier exemple représenté ci-contre à partir de la courbe de traction d'un acier : pour une valeur εo de la déformation on pourra obtenir la contrainte σ1 si l'on y est arrivé directement, et σ2 s'il y a eu un retour en arrière.
En anticipant un peu, un second exemple nous est fourni par un modèle de Maxwell
pour lequel on pourra écrire (>).
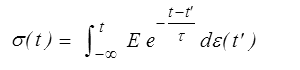
De manière générale on écrira
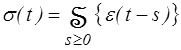
exprimant que la contrainte à l'instant t dépend de toutes les valeurs passées de la déformation.
Dans un jargon plus technique, on parle d'une fonctionnelle héréditaire causale :
- fonctionnelle, c'est ainsi que les mathématiciens appellent souvent une fonction dont l'argument est lui-même une fonction : la contrainte est une fonction de la fonction qui donne l'histoire de la déformation ε ( t − s ) pour tout s ≥ 0.
L'accolade est ici utilisée (plutôt qu'une simple parenthèse) pour souligner également cette dépendance fonctionnelle. - héréditaire, car la contrainte dépend de tout ce qu'a subi le matériau. Le matériau a une mémoire.
- causale, car seule intervient l'histoire passée et non l'histoire à venir.
De manière complètement symétrique on peut également écrire
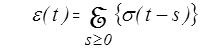
donnant la déformation en fonction de l'histoire de la contrainte.
Modèles de Comportement
Sauf cas particulier, on n'explicitera jamais cette fonctionnelle. Il convient toutefois de bien conserver à l'esprit cette forme générale.
Un modèle de comportement est un algorithme permettant à chaque instant de calculer la contrainte en fonction de l'histoire des déformations ou vice-versa.
Cette relation fonctionnelle pourra dans la pratique prendre des formes très diverses.
Considérons par exemple le cas du fluide visqueux évoqué précédemment : en petites perturbations, le tenseur des taux de déformation est la dérivée par rapport au temps de la déformation et ρ pourra s'exprimer à partir de la déformation. On pourra donc écrire
σ = σ ( ε , )
cas particulier de la première forme générale ( déformation -> contrainte ) puisque, si l'on connaît ε ( t − s ) pour tout s, on peut bien évidemment connaître sa dérivée.
Pour la seconde forme ( contrainte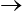 
déformation ) la situation apparaît plus complexe, car la loi ne donne pas directement la déformation. Toutefois elle pourra, en principe, s'inverser en une relation ( σ , ε ) qui, connaissant l'histoire de σ, permettra de déterminer ε(t) par intégration de l'équation différentielle correspondante. De même la loi intégrale citée plus haut pour le modèle de Maxwell explicite directement la première forme. La seconde forme demande d'inverser cette relation. Nous verrons plus loin comment faire.
Quant à traduire en relation mathématique la courbe de traction avec décharge telle que nous l'avons décrite plus haut, c'est un des défis qu'il nous faudra relever.
Remarquons aussi que, ainsi considérée, la Mécanique des Matériaux pourrait apparaître comme un simple chapitre de la théorie des Systèmes développée depuis bien longtemps en Automatique. Effectivement nous retrouverons plus loin certains outils développés dans ce cadre (>), mais contrairement à ce que l'on a pu un temps espérer cet apport restera marginal.