Le cas indépendant des vitesses
Potentiel indépendant des vitesses
Nous avons donc vu que le patin plastique posait problème pour le calcul de 
= x en fonction de σ = X. En fait ce problème est générique et découle directement du comportement indépendant des vitesses. Le lecteur effrayé par le caractére un peu abstrait de cette page pourra toutefois passer directement à son application à la plasticité (>)
, quitte à revenir ici plus tard.
Dans ce cadre en effet un comportement indépendant des vitesses sera défini par la condition
X( λ x ) = X( x ) ∀ λ ≥ 0
La fonction X est positivement homogène de degré zéro, c'est-à-dire inchangée si l'on multiplie le flux (c'est-à-dire, pour nous, la vitesse) par un scalaire positif quelconque (donc en accélérant ou ralentissant le processus). Le potentiel de dissipation Ω est alors positivement homogène de degré 1
Ω( λ x ) = λ Ω( x ) ∀ λ ≥ 0
Il est alors bien évident que l'on ne peut pas calculer x en fonction de X, puisque tous les x appartenant à une demi-droite correspondent à une même valeur de X. On ne peut donc pas écrire la loi inverse et a fortiori construire le potentiel de dissipation ω( X ).
Comme souvent en mathématiques, on va contourner l'obstacle en généralisant la notion de fonction, de dérivée et de transformation de Legendre, et en se plaçant dans le cadre de l'analyse convexe (w), qui permet d'étendre tout ce qui précède.
On peut en particulier montrer que si la fonction Ω( x ) est convexe et positivement homogène de degré 1, alors le potentiel ω (sa fonction convexe conjuguée) est la fonction indicatrice d'un domaine convexe C dans l'espace X (c'est-à-dire qui vaut 0 dans C et +∞ à l'extérieur; les fonctions convexes peuvent valoir +∞).
Loi d'évolution et sous-différentiel
A l'intérieur de C la fonction ω est constante et sa dérivée est donc nulle
X intérieur à C => x = 0
A l'extérieur x n'existe pas, et c'est un domaine interdit pour X. Sur la frontière par contre, il pourra exister plusieurs valeurs de x. La dérivée devient alors un ensemble appelé sous-différentiel (w) et qui est complètement défini par la propriété suivante :
Sous-différentiel.
Si ω est la fonction indicatrice du convexe C, les flux x possibles pour une force X sont définis par
x .( X − X*) ≥ 0 ∀ X*∈ C
On tire en particulier de cette inégalité que
- si X est à l'intérieur de C alors x est nul ;
- si X est sur la frontière de C en un point régulier (tangente continue), alors x est dirigé selon la normale extérieure à C ;
- si X est sur un point anguleux de la frontière, alors x appartient au cône des normales (le cône limité par les normales aux différentes faces constituant le coin).
Ces résultats sont schématisés par la figure ci-dessous.
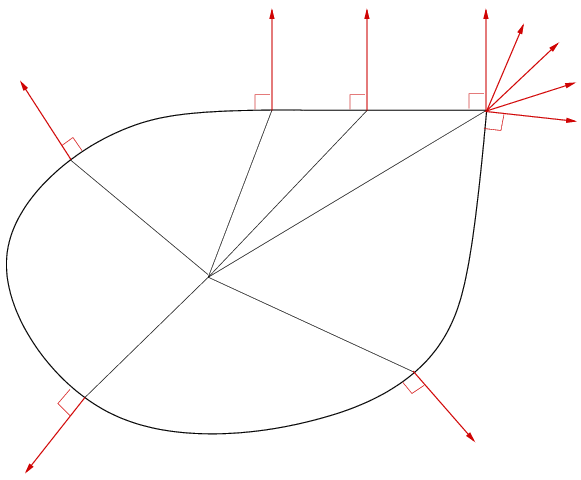
On remarquera la simplicité et l'extrême économie de moyens que permet cette formulation. Appliquée à la plasticité les initiés auront reconnu le « principe du travail maximal » (>) .
Cas d'une fonction seuil
Si le convexe C est suffisamment régulier, alors on pourra le définir par l'intermédiaire d'une fonction f ( X ) dérivable telle que C soit défini par l'inégalité
X ∈ C <=> f ( X ) ≥ 0
La frontière est alors définie par f ( X ) = 0 tandis que l'intérieur de C est défini par f ( X ) < 0.
La loi d'évolution s'écrira alors :
Loi d'évolution.
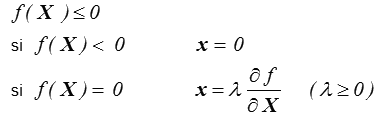
La fonction f ( X ) est appelée function seuil et le scalaire λ ≥ 0, indéterminé par la loi d'évolution, est appelé multiplicateur plastique.
D'un point de vue pratique, on retiendra que pour un comportement des vitesses régulier il convient simplement de remplacer la relation x = ∂ ω / ∂ X par la loi dévolution que nous venons d'écrire.
Ce formalisme définit le cadre des matériaux standard généralisés. Ce n'est pas une loi physique, et contrairement aux relations d'Onsager, on rencontrera des situations où il faudra rejeter cette hypothèse, mais même dans ce cas ce formalisme apportera souvent une première approche très féconde.