Thermodynamique des processus irréversibles
Irréversibilité - Dissipation
Dans sa formulation traditionnelle, la thermodynamique porte mal son nom et il vaudrait mieux parler de thermostatique.
D'une part elle se limite usuellement à des processus suffisamment lents pour que l'on puisse négliger l'énergie cinétique − elle se situe donc dans le cadre quasi statique tel que nous l'avons défini en MMC (<). Sinon, comme nous l'avons déja vu (<) l'énergie cinétique intervient au même titre que l'énergie interne dans le premier principe de la thermodynamique. .
D'autre part, et c'est ce qui nous importe ici, elle étudie principalement les états d'équilibre thermodynamique et donc principalement les évolutions réversibles pour lesquelles le second principe se ramène à une égalité. Dans le cas irréversible elle constate une inégalité mais s'arrête à peu près là.
Pour aller plus loin, il faut aborder un autre chapitre : la TPI, Thermodynamique des Processus (ou des Phénomènes) Irréversibles, en général non traité dans les exposés classiques. Il s'agit pourtant là d'un chapitre important et aux multiples applications.
Le point de départ en est toujours la dissipation ou production interne d'entropie que, de manière générale, on pourra décrire sous la forme d'un produit scalaire
ø = X . x
Les forces thermodynamiques X mesurent l'écart à l'équilibre, tandis que les flux thermodynamiques x traduisent une vitesse de retour à l'équilibre ou un taux d'évolution induite par ce déséquilibre.
Forces et flux thermodynamiques
Ainsi la première étape dans la mise en oeuvre de la TPI est le calcul de la dissipation et l'identification des forces thermodynamiques et des flux associés.
Dans nos problèmes de rhéologie nous partirons de la dissipation (<)
ø = σ .  −
− 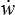
où le produit scalaire σ .  représente
représente
- le produit usuel pour une sollicitation uniaxiale,
- le produit contracté σij
 ij dans le cas général.
ij dans le cas général.
Si par exemple l'énergie est nulle (système purement dissipatif) on identifie directement X à la contrainte et x à la vitesse de déformation
X = σ x = 
Plus généralement, l'identification de X et x se fera naturellement sitôt que l'on aura choisi la forme de l'énergie et nous aurons l'occasion d'en voir maints exemples. On notera que, dans ce cas, le flux thermodynamique est une dérivée par rapport au temps.
La situation est un peu différente dans le cas de la conduction thermique. On montre alors que la dissipation associée est
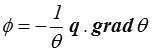
où, au coefficient (−1/θ) près, la force thermodynamique est le gradient de température (l'équilibre thermique exige une température uniforme). Ce déséquilibre thermique induit un flux de chaleur q du chaud vers le froid, qui vise à rétablir l'équilibre thermique. La conduction thermique est un phénomène irréversible et la dissipation ne s'annule que dans les deux cas limites d'un matériau parfaitement conducteur (grad θ = 0, température uniforme) ou parfaitement isolant (q = 0).
On retrouvera une situation analogue dans tous les problèmes de diffusion :
- Ecoulement en milieu poreux
force : gradient de pression
flux : vitesse de filtration - Diffusion d'espèce
force : gradient de concentration
flux : vitesse de diffusion - Conduction électrique
force : gradient du potentiel électrique
flux : intensité du courant.
Mentionnons également l'analyse des réactions chimiques où la force thermodynamique est l'affinité de la réaction et le flux la vitesse de réaction.
Relations d'Onsager
La TPI classique consiste alors à relier forces et flux, et, dans sa version la plus simple, à écrire une relation linéaire
X = L x ou x = l X l = L−1
où L ou l est un opérateur linéaire, c'est-à-dire en fait, en travaillant en composantes, une matrice.
On fait alors l'hypothèse que cette matrice est symétrique
L = LT ou l = l T
Au départ cette symétrie a été démontrée dans un cas très particulier par un raisonnement de physique statistique. Elle a ensuite été formellement généralisée et appliquée à toute une variété de situations physiques. Il est toutefois remarquable que, bien que d'origine purement empirique, cette extension n'ait semble-t-il jamais été contredite par l'expérience.
C'est ce que l'on appelle usuellement les relations d'Onsager (stricto sensu les relations d'Onsager consistent en fait dans la symétrie de la matrice). La matrice L (ou l ) est souvent appelée « matrice des coefficients phénoménologiques » soulignant ainsi le caractère empirique de cette approche.
Empirique mais remarquablement efficace, c'est en particulier cette approche qui, appliquée par exemple à la conduction thermique, conduit à la loi de Fourier
qi = − kij ∂θ / ∂xj
avec un tenseur de conductivité thermique symétrique qui, dans le cas isotrope, se réduit à un scalaire.
On obtient de même
- pour la diffusion d'espèce, la loi de Fick,
- pour les milieux poreux, la loi de Darcy,
- pour la conduction électrique, la loi d'Ohm.
Ce sont également elles qui conduisent en Mécanique des Fluides au fluide visqueux newtonien et aux équations de Navier-Stokes (<) .
Potentiel de dissipation
Une manière commode d'imposer cette symétrie est de définir, plutôt qu'une matrice L ou l , une forme quadratique
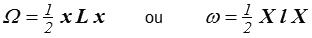
imposant automatiquement la symétrie de la matrice correspondante L ou l . Les relations forces - flux s'écrivent alors simplement
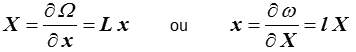
Les fonctions Ω et ω sont appelées potentiels de dissipation. On remarque aussi que si l'on s'intéresse à la valeur des fonctions Ω(x) et ω(X) on peut alors écrire
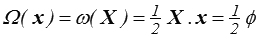
Les deux potentiels de dissipation représentent la moitié de la dissipation ø considérée comme fonction de X ou x.
On notera qu'il ne s'agit ici que d'une commodité d'écriture. On notera aussi que les deux fonctions Ω(x) et ω(X), formes quadratiques semi-définies positives, sont des fonctions convexes.
Une variante
Les relations d'Onsager imposent la symétrie de la matrice reliant les forces aux flux ou bien les flux aux forces. Il est toutefois parfois commode ou nécessaire de n'utiliser comme variables de base ni l'ensemble des forces, ni l'ensemble des flux, mais plutôt une combinaison des deux. Nous décomposons donc l'ensemble des forces et des flux en deux groupes

et nous choisissons d'écrire les relations de dissipation comme donnant X1 et x2 en fonction de x1 et X2
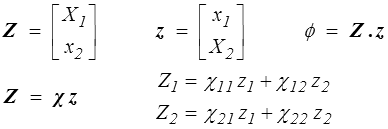
La matrice χ doit alors vérifier les relations
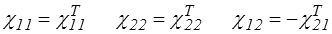
c'est-à-dire symétrie prévisible pour les blocs diagonaux mais antisymétrie plus inattendue pour les blocs non diagonaux. On parle alors des relations de réciprocité de Casimir-Onsager. Pour démontrer ces relations il suffit de partir de la relation initiale symétrique
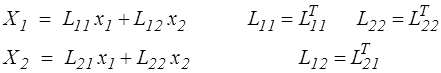
et d'en faire une inversion partielle pour calculer X1 et x2 en fonction de x1 et X2
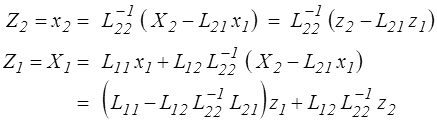
ce qui donne pour la matrice χ
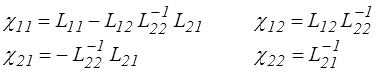
et d'après les relations de symétrie pour les matrices Lij, celles pour les matrices χij.
La dissipation s'écrit alors
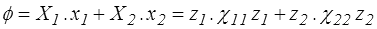
On peut encore construire un potentiel de dissipation χ(x1 , X2 ) en passant par une transformation de Legendre partielle
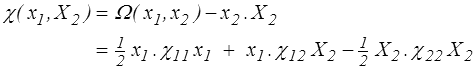
qui permet d'écrire
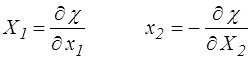
avec un pseudo-potentiel χ quadratique mais qui, même dans le cas linéaire, n'a plus aucun rapport avec la fonction de dissipation.
