Plasticité des métaux
Les matériaux métalliques sont très largement utilisés et ceci suffit pour justifier une présentation plus détaillée. Mais de façon plus générale cet exemple, même déjà passablement simplifié, nous donnera une idée de la complexité et de la diversité des phénomènes que l'on peut rencontrer et qu'il faudrait être capable de modéliser.
Courbe de traction
Nous avons déjà décrit (<) la courbe de traction d'un matériau métallique : comportement élastique (linéaire, réversible) jusqu'à la limite élastique, puis comportement plastique au-delà (irréversibilité, déformation résiduelle lorsqu'on relâche la contrainte, décharge élastique).
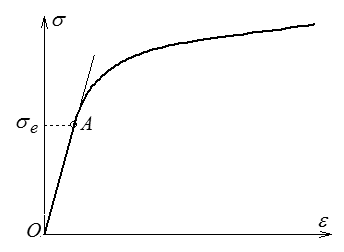
C'est en fait le comportement caractéristique des matériaux cristallins, l'élasticité résulte de la déformation (réversible) du réseau cristallin, tandis que la plasticité est la manifestation macroscopique du mouvement (irréversible) des dislocations.
Nous avons déjà évoqué (<) le caractère conventionnel de la limite élastique, la plastification ne se produisant en général que de manière très progressive, au fur et à mesure par exemple que les sources de Frank et Read commencent à émettre des boucles de dislocations. Une exception toutefois, les aciers doux pour lesquels la transition fait apparaître un « palier » plastique qui, lorsque l'on y regarde de plus près, correspond en fait à une succession d'instabilités dont l'origine physique est connue (bande de Lüders).

La plasticité s'accompagne également d'un « écrouissage » (augmentation de la limite élastique) qui résulte notamment de l'accumulation des dislocations, qui rend plus difficile leur mouvement ultérieur.
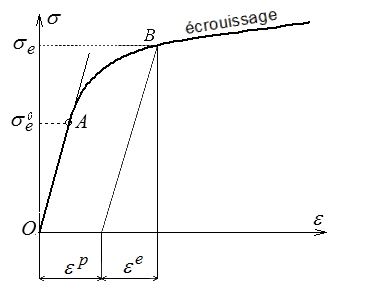
On appelle déformation plastique la déformation permanente ou résiduelle qui subsiste après relâchement de la contrainte et on écrira
ε = ε e + ε p σ = E ε e
Courbe rationnelle de traction
Pour obtenir la courbe de traction on mesure la force appliquée P et la variation de longueur Δl que l'on ramène à la section et la longueur initiale de l'éprouvette, pour obtenir contrainte et déformation
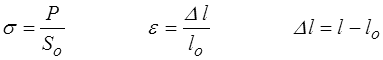
Toutefois la force appliquée s'applique en réalité à la section réelle S de l'éprouvette, qui du fait de la contraction transversale est plus petite que So. On appelle « contrainte vraie » cette contrainte
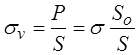
la contrainte σ étant alors souvent appelée la « contrainte nominale » (en anglais, σv = true stress, σ = engineering stress).
De même, mais pour des raisons bien plus obscures, on appelle « déformation vraie » la déformation logarithmique
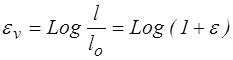
Je renonce à reproduire les arguments traditionnellement mis en avant pour ce choix et que je trouve, pour ma part, peu convaincants. En fait, la justification profonde de ce choix apparaîtra plus tard lorsque nous étudierons les grandes déformations.
La courbe rationnelle de traction s'obtient donc en traçant (pour autant qu'on puisse le faire, c'est-à-dire moyennant quelques approximations) σv en fonction de εv. Tant que les déformations restent petites cela n'a bien évidemment aucune importance car au premier ordre σv = σ et εv = ε, et nous nous limitons dans ce cours au cas des petites perturbations. Néanmoins, il sera souvent tentant d'extrapoler aux grandes déformations. On retiendra simplement, en attendant d'en savoir plus, que cette extrapolation sera souvent légitime à condition d'utiliser les déformations logarithmiques.
On peut couramment atteindre, dans un essai de traction, des déformations de 20 ou 30% et parfois même bien au-delà. Ces déformations sont toutefois limitées par la striction (localisation de la déformation par étranglement).
On considère assez raisonnablement que pour les matériaux métalliques le comportement en compression est symétrique du comportement en traction. Toutefois l'essai de compression ne comporte pas de striction (la section augmente au lieu de diminuer). On a représenté sur la figure ci-dessous les courbes de traction et de compression correspondant à la même courbe rationnelle de traction. En traction la contrainte nominale passe par un maximum à la striction, alors qu'elle croît toujours en compression.
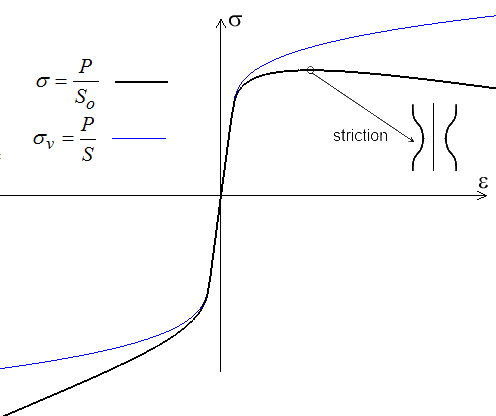
Il serait donc tentant d'utiliser toujours l'essai de compression plutôt que l'essai de traction. Malheureusement il pose d'autres problèmes : éprouvette courte pour éviter le flambement, frottement nul à la paroi, donc lubrification (<) , etc...
Comportement cyclique
La courbe de traction (ou de compression) correspond à un chargement monotone : on applique une contrainte (ou une déformation, peu importe si le comportement est indépendant des vitesses) croissante au cours du temps. Or les structures réelles sont le plus souvent soumises à des sollicitations alternées. C'est le domaine de la plasticité cyclique.
Considérons par exemple un essai cyclique à déformation imposée, entre +ε o et − εo. Après avoir allongé l'éprouvette jusqu'à +ε o (allongement élastique sur OAo puis plastique sur AoBo) on revient en arrière jusqu'à − εo. La courbe de décharge correspondante BoA'oB'o fait encore apparaître un retour élastique BoA'o suivi d'une compression plastique A'oB'o. On obtient à nouveau un comportement élastique (linéaire, réversible) tant que la contrainte reste dans le nouveau domaine élastique
σ(A'o ) < σ < σ(Bo ) σ ∈ ] σ(A'o ) , σ(Bo ) [

et si l'on compare ce nouveau domaine élastique au domaine élastique initial (symétrique)
− σ(Ao ) < σ < σ(Ao )
on constate que si σ(Bo ) > σ(Ao ) (c'est, on l'a vu plus haut, l'écrouissage) on aura très souvent
− σ(A'o ) < σ(Ao )
C'est ce que l'on appelle l'effet Bauschinger : un écrouissage en traction augmente la limite élastique en traction mais diminue la limite élastique en compression.
La contrainte de compression − σ(B'o ) atteinte pour ε = − εo est par contre voisine de la contrainte de traction σ(Bo ) obtenue pour ε = + εo et donc, par la symétrie traction-compression, voisine aussi de celle que l'on aurait obtenu dans un essai de compression direct (courbe pointillée).
Si ensuite on impose à nouveau un allongement de − εo jusqu'à + εo, on obtient une courbe B'o A1B1, élastique sur B'o A1 puis plastique sur A1B1, pour arriver finalement pour ε = εo à une contrainte σ(B1 ) voisine de σ(Bo ).
Le comportement observé lors des cycles ultérieurs est similaire avec évolution lente de la boucle de contrainte-déformation qui, au bout d'un nombre suffisant de cycles, finit par se stabiliser sur un cycle limite correspondant à une boucle d'hystérésis.
On réalise cet essai pour diverses amplitudes de déformation Δε = 2 εo et on mesure la demi-amplitude de contrainte au cycle limite. On obtient ainsi la courbe d'écrouissage cyclique donnant Δσ / 2 en fonction de Δε / 2. Cette courbe (bleue) est souvent au-dessus de la courbe de première charge (noire) − on parle alors de durcissement cyclique, mais il peut arriver qu'elle soit en-dessous (radoucissement cyclique).
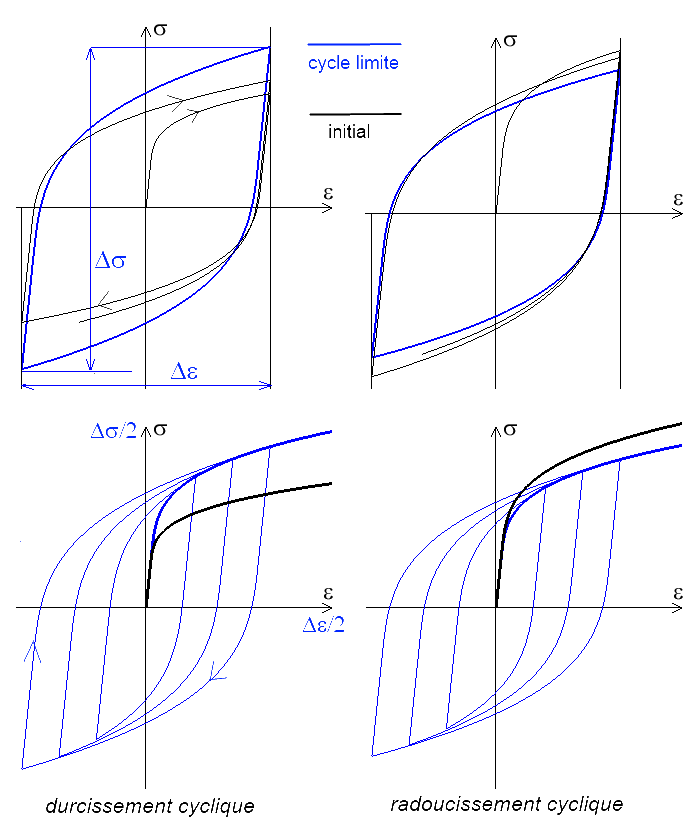
Cyclage en contrainte
Dans le cas d'une sollicitation analogue, mais à contrainte imposée (cyclage symétrique en contrainte, la contrainte évolue entre + σo et − σo ), on obtient un comportement analogue, avec toutefois une situation limite un peu plus complexe.
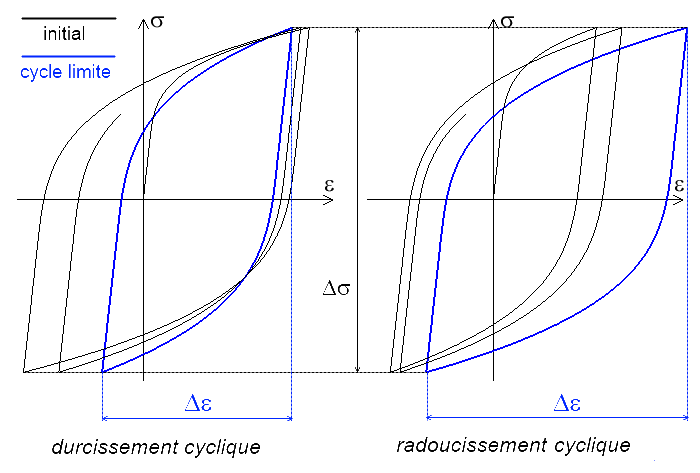
Il existe encore un cycle limite mais il est non centré en déformation. On tracera néanmoins la courbe d'écrouissage cyclique (Δσ / 2) en fonction de (Δε / 2), et on considère en général que la courbe d'écrouissage cyclique ainsi obtenue est la même que celle résultant d'essais à déformation imposée.
On peut également envisager des sollicitations cycliques non centrées. Pour un chargement à déformation imposée (ε imposé variant entre εm − Δε / 2 et εm + Δε / 2 avec εm ≠ 0) on considère habituellement que le comportement limite observé est, pour un Δε donné, le même que dans le cas centré ( εm = 0 ), avec un simple décalage en ε du cycle-limite.
La situation sous contrainte imposée (σ varie entre σm − Δσ / 2 et σm + Δσ / 2) est toute différente, et l'on verra souvent apparaître un phénomène de « rochet », correspondant à un cycle limite non fermé qui se décale progressivement vers la droite (augmentation de la déformation ) si σm > 0.
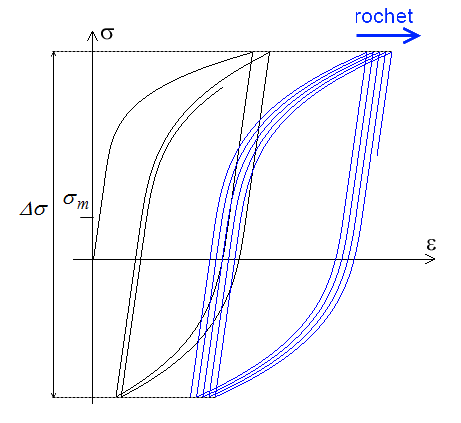
Peut-on observer un tel phénomène de rochet pour une sollicitation centrée (σm = 0) ? Cette question a été et reste sans doute encore débattue. Toutefois je n'ai jamais vu en faveur de ce rochet (pour σm = 0) d'évidence vraiment convaincante, et j'aurais donc tendance à croire que non.
Pour construire la courbe d'écrouissage cyclique, il faut en principe réaliser toute une série d'essais pour diverses valeurs de Δσ ou Δε. Une pratique courante consiste toutefois à se limiter à un seul essai à plusieurs niveaux : on impose une sollicitation cyclique à un premier niveau Δσ1 (ou Δε1), on attend la stabilisation, puis on augmente le niveau, on obtient une nouvelle évolution du cycle que l'on suit jusqu'à stabilisation, et ainsi de suite. Cette pratique est en général considérée comme légitime. On obtiendrait par contre un comportement très différent si l'on procédait par niveaux décroissants.
Plus généralement, le comportement sous sollicitations cycliques à plusieurs niveaux met en évidence des comportements très complexes et encore mal compris.
Remarquons aussi que nous nous sommes ici limités à un comportement « uniaxial » (essai de traction par exemple). Le comportement cyclique biaxial ou multiaxial (traction-torsion par exemple) conduit lui aussi à des comportements complexes et encore mal compris.
Fatigue
Les sollicitations cycliques évoquées plus haut impliquent une plastification alternée (extension-compression) à chaque cycle. Elles conduisent rapidement à la rupture. On parle de fatigue à faible nombre de cycles ou fatigue oligocyclique. Au contraire, une sollicitation cyclique de niveau plus faible et inférieur à la limite élastique n'entraîne pas de modification apparente du comportement, mais conduit néanmoins à la rupture au bout d'un nombre élevé de cycles (fatigue à grand nombre de cycles). Ce phénomène a fait l'objet de nombreuses études en science des matériaux, il reste encore imparfaitement compris et mal modélisé d'un point de vue mécanique. Nous aurons dans la suite l'occasion d'évoquer certains aspects de cette problématique, sans toutefois l'aborder de front.
