Modèlisation en Viscoélasticité
Les modéles que nous venons de voir sont des modéles particuliers, souvent utiles. Convenablement généralisés, ils peuvent aussi permettre une description beaucoup plus précise et règlable du comportement viscoélastique des matériaux réels, notamment des polymères.
Modèle série généralisé
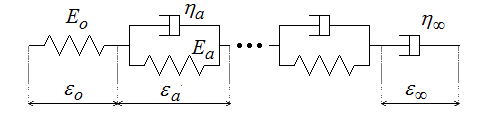
Le modèle série généralisé correspond au montage en série d'un ressort, d'un amortisseur et de n modèles de Kelvin (Il est souvent appelé modèle de Maxwell généralisé, mais je n'aime pas cette terminologie).
D'un point de vue thermodynamique on écrira donc
La dissipation est
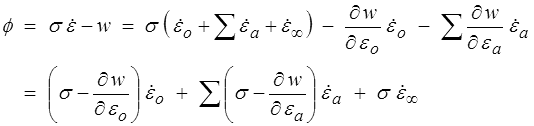
Les forces et les flux thermodynamiques sont
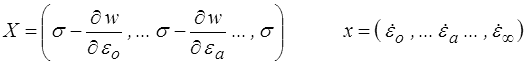
La relation force-flux s'écrit donc
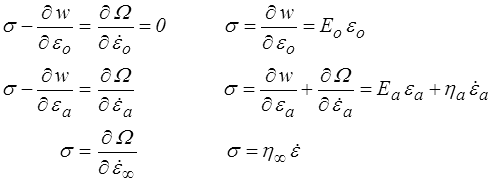
On peut alors calculer la fonction de fluage, mais il est plus simple de remarquer que la fonction de fluage d'un montage série est la somme des fonctions de fluage des éléments. On écrira donc
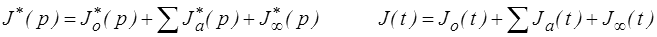
soit, compte tenu des résultats obtenus plus haut pour le modèle de Kelvin,
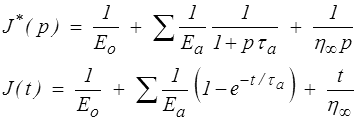
et nous renonçons à calculer la fonction de relaxation (fraction rationnelle en p assurément, donc E (t) est théoriquement calculable, mais ce serait lourd).
Modèle parallèle généralisé
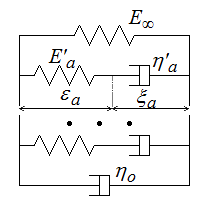Le modèle parallèle généralisé (ou Kelvin généralisé) correspond au montage parallèle d'un ressort, d'un amortisseur et de n modèles de Maxwell.
D'un point de vue thermodynamique on écrit
avec
ε = εa + ξ a
La dissipation sera alors
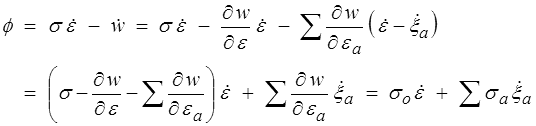
où l'on a posé
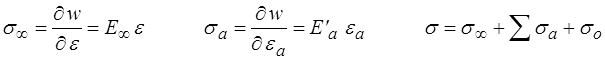
Les contraintes σ∞, σa et σo correspondent aux contraintes respectivement transmises par le ressort E∞ , la branche de Maxwell a et l'amortisseur ηo.
Les forces et les flux thermodynamiques sont
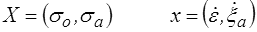
et la relation force-flux s'écrit
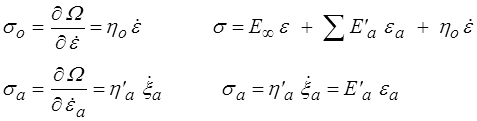
loi de comportement naturelle du montage parallèle.
La fonction de relaxation de ce modèle s'obtient simplement en remarquant que la fonction de relaxation d'un montage parallèle est la somme de celles de ses éléments et en utilisant le résultat obtenu pour le modèle de Maxwell
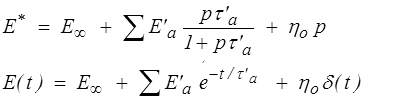
avec une masse de Dirac associée à l'amortisseur ηo.
Fluides et Solides
Le comportement différé, c'est-à-dire pour des temps longs ou des sollicitations lentes, s'obtient directement par la limite t 
∞ ou p 0.
Pour le modèle série généralisé par exemple on obtient directement à cette limite
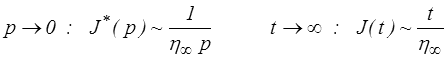
ce qui correspond à un amortisseur de viscosité η∞. L'amortisseur en série de l'ensemble contrôle le comportement et le matériau « flue » (s'écoule indéfiniment, c'est le sens originel du mot fluage). C'est un fluide.
Si par contre l'amortisseur en série est absent, comme par exemple pour le modèle de Poynting, alors ces formules deviennent
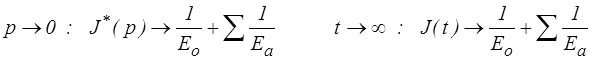
ce qui correspond à un ressort dont la rigidité E∞ est donnée par
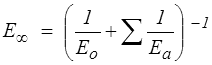
la déformation se stabilise et le matériau se comporte comme un solide.
L'approche est similaire pour le modèle parallèle généralisé
soit un comportement de type solide sauf si le ressort célibataire E∞ est absent, auquel cas il vient
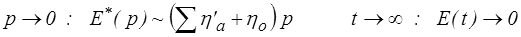
A propos des notations, on voit ici pourquoi nous avons pour le modèle parallèle généralisé muni d'un prime tous les coefficients ( E'a , η'a , τ'a = η'a / E'a ): ceci nous permet de distinguer pour pouvoir les comparer, comme nous l'avons fait pour Zener et Poynting, les modèles série et parallèle généralisés. Par ailleurs, la transformée de Laplace-Carson est ici essentielle pour reconnaître dans ce comportement limite un amortisseur de viscosité
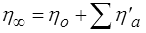
et donc un comportement fluide
La fonction E (t) tend simplement vers zéro sans nous donner d'information directe sur ce comportement asymptotique. Pour le mettre en évidence, il faudrait considérer un autre essai, par exemple un essai de traction à vitesse constante.
Une première classification des modèles viscoélastiques, fluide ou solide, peut donc se faire d'après le comportement différé.
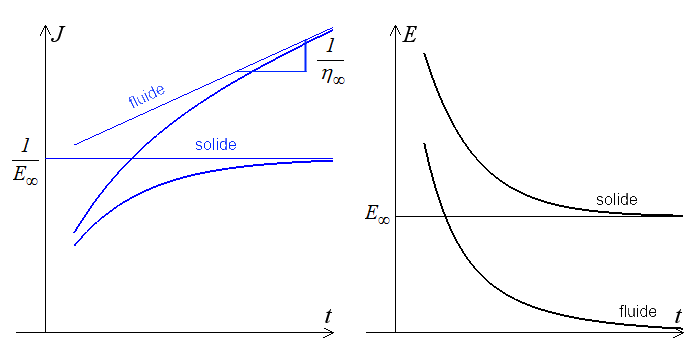
Viscosité et élasticité instantanée
On caractérise de manière symétrique le comportement instantané (temps petits ou sollicitations rapides) en examinant la limite t 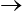0 ou p ∞.
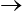Partant du modèle série généralisé on obtient
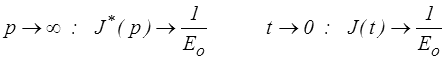
le modèle se comporte comme un ressort de rigidité Eo (élasticité instantanée).
Si par contre le ressort célibataire Eo est absent, alors on obtient
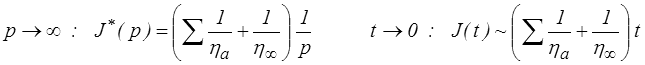
ce qui correspond à un amortisseur de viscosité
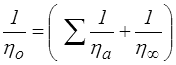
c'est-à-dire à un comportement visqueux réagissant à une contrainte brutalement appliquée par un saut de vitesse de déformation, la déformation elle-même restant continue.
Pour le modèle parallèle généralisé on obtient de même
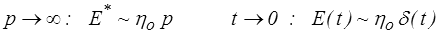
L'essai de relaxation n'est pas possible et le modèle se comporte comme un amortisseur de viscosité ηo (modèle visqueux).
Si par contre l'amortisseur célibataire est absent, alors
Le modèle se comporte comme un ressort de rigidité
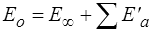
Une seconde classification résulte donc du comportement instantané, visqueux ou élastique.
En combinant ces deux critères on obtient une classification des comportements viscoélastiques en 4 grandes classes .
Modèle de Biot
On pressent, et on peut effectivement démontrer comme nous l'avons fait pour Zener et Poynting, que ces deux modèles série et parallèle généralisés ne sont en fait que deux représentations du même comportement viscoélastique. Il faut gérer avec soin, à partir des comportements instantané et différé, l'absence ou la présence des éléments célibataires, mais on peut ensuite utiliser indifféremment l'un ou l'autre et choisir le plus commode : parallèle généralisé sous déformation imposée, série généralisé si c'est la contrainte qui est imposée.
Plus généralement, on peut montrer que tout modèle standard généralisé (<) linéaire (modèle de Biot), donc en particulier tout modèle rhéologique constitué d'un assemblage quelconque de ressorts et d'amortisseurs, peut être représenté par l'un ou l'autre, au choix, de ces deux modèles.
La démonstration est un peu technique mais le principe est assez simple : un modèle de Biot est défini par les deux formes quadratiques donnant respectivement l'énergie w (ε, α) et le potentiel de dissipation Ω (
, 
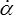) où α désigne les variables internes. Les modèles série et parallèle généralisés correspondent dans ce cadre à deux formes diagonales des matrices représentatives de ces formes quadratiques. Or on sait diagonaliser simultanément deux formes quadratiques; il suffit alors de se reporter au chapitre correspondant d'un cours d'algèbre linéaire.
Spectre de fluage et de relaxation
Considérons par exemple un solide élastique, le modèle série correspondant est donc
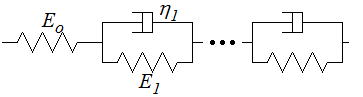
et sa fonction de fluage est
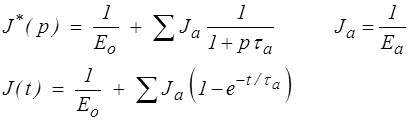
En augmentant à l'infini le nombre de modèles de Kelvin, cette somme finie deviendra une intégrale par rapport au temps de fluage τ. On écrira donc
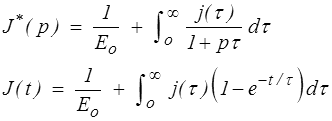
la fonction j (τ) est alors appelée spectre de fluage ou spectre de retard du matériau.
De même, partant du modèle parallèle généralisé
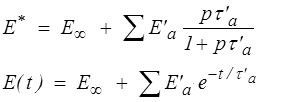
et par passage à un spectre continu
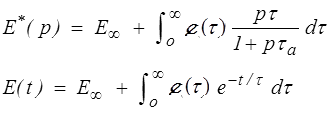
avec un spectre de relaxation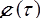 
.
Ainsi nos modèles rhéologiques série ou parallèle généralisés peuvent-ils être aussi considérés comme des discrétisations d'un modèle continu défini par son spectre de fluage ou de relaxation.
Par ailleurs on peut montrer (mais ce sont ici des mathématiques nettement plus difficiles) que toute fonction J (t) ou E (t) raisonnable peut être représentée sous forme spectrale et donc discrétisée par un modèle rhéologique. Il existe, je crois, des méthodes numériques permettant cette discrétisation à partir d'une fonction E (t) ou J (t) obtenue expérimentalement. Pour les applications cela reste toutefois, à ma connaissance, une approche marginale à ce niveau.
D'un point de vue fondamental, par contre, nous pouvons considérer que ces modèles rhéologiques permettent une description à peu près complète des comportements viscoélastiques.