Viscoélasticité tridimensionnelle
Loi de comportement
Contrairement à ce qui se passera pour les autres types de comportement, l'écriture d'une loi de comportement tridimensionnelle ne présente pas ici de difficulté particulière. Le principe de superposition de Boltzmann (<) qui nous a servi de point de départ s'applique également aux différentes composantes du tenseur des déformations ou des contraintes. En sommant la contribution de chacune des composantes la loi héréditaire s'écrira simplement
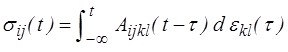
extension naturelle de la loi monodimensionnelle (<) . Les 21 coefficients de la loi élastique sont donc à remplacer par 21 fonctions de relaxation. Ces fonctions pourront en principe être déterminées expérimentalement par des essais de relaxation excitant séparément les diverses composantes.
En transformée de Laplace-Carson, ces relations se simplifient en
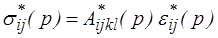
loi formellement identique à la loi élastique, ce que nous exploiterons plus tard.
De même on introduira, pour caractériser le comportement harmonique, 21 modules complexes
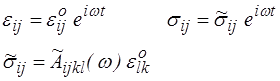
Ce n'est pas nécessairement très simple, mais en tout état de cause pas beaucoup plus difficile qu'en élasticité.
On peut également utiliser la formulation inverse introduisant les souplesses ou complaisances. Les lois précédentes deviennent respectivement
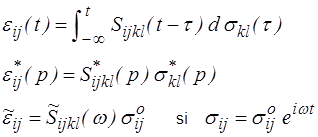
Viscoélasticité isotrope
Comme en élasticité cela devient beaucoup plus manipulable dans le cas isotrope, et la loi de comportement (<) devient alors, en considérant par exemple l'écriture opérationnelle (en transformée de Laplace-Carson, mais les écritures complexes et héréditaires s'écriront de manière analogue)
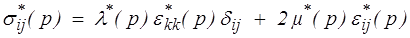
ou, comme nous l'avons vu dans le cas élastique, toute autre forme équivalente. Nous privilégierons toutefois l'écriture en partie sphérique / déviateur (<) qui est, comme nous le verrons bientôt, la plus porteuse de sens physique. Nous écrirons donc

Un modèle viscoélastique isotrope résulte de la combinaison de deux modèles monodimensionnels décrivant le comportement en contraction isotrope et glissement simple respectivement.
Le comportement en traction simple, plus facile à suivre expérimentalement, s'en déduira directement en écrivant
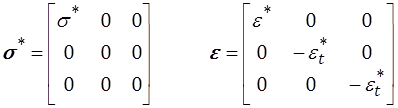
et, en m'autorisant − temporairement − à omettre les étoiles,
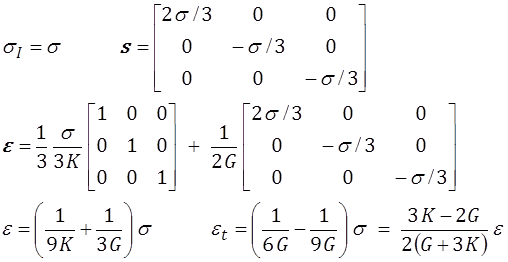
Soit, en réintroduisant les étoiles,
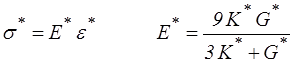
La réalisation d'un essai de fluage ou de relaxation donnera E(t) ou E *(p). Si on mesure en plus la contraction transversale εt (t) on en tirera une seconde information qui nous permettra de séparer dans E * les deux modules élémentaires K * et G *.
Pour éviter cette détermination on fait souvent l'une ou l'autre des deux hypothèses suivantes.
Hypothèse 1.
Les deux modules E et G ont le même comportement temporel
E(t) = Eo φ(t) G(t) = Go φ(t).
Le rapport εt /ε reste alors constant et on peut encore parler du coefficient de Poisson
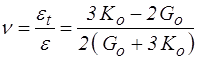
Hypothèse 2.
La viscoélasticité n'intervient que sur la partie déviatoire
K(t) = Ko G(t) quelconque.
Le rapport εt /ε évolue alors au cours du temps mais sa mesure instantanée (t → 0) ou différée (t → ∞) suffit pour compléter l'information donnée par E(t) et obtenir un modèle isotrope complet.
Classification des comportements
Nous avons présenté, dans le cas monodimensionnel, une classification selon deux critères
Un modèle tridimensionnel isotrope est constitué de deux modèles monodimensionnels décrivant respectivement le comportement en compression hydrostatique et en glissement simple. La classification des comportements tridimensionnels isotropes se fera donc tout naturellement par « produit » de ces deux classifications, conduisant en principe à 4x4 types de comportement.
Tous ne sont pas raisonnables. En particulier
le comportement en compression hydrostatique est nécessairement de type solide
K(t) → K∞ pour t → ∞. Si l'on impose par exemple une pression constante (fluage en compression hydrostatique) alors le volume va éventuellement diminuer mais finira par se stabiliser. L'hypothèse 2 évoquée plus haut consiste d'ailleurs à négliger cette évolution. La distinction fluide/solide porte donc uniquement sur le comportement déviatoire.
Cette propriété met aussi en évidence une limitation majeure de l'hypothèse 1 qui ne peut en effet être pertinente que pour un comportement de type solide.
Nous n'insisterons pas davantage ici, une discussion approfondie de cette distinction entre fluide et solide ne pourra être abordée sérieusement que dans un contexte autorisant les grandes déformations qui sont ici exclues. En fait cette distinction sera au cœur du cours sur les grandes transformations. Toutefois, même si l'interprétation donnée ici reste simpliste et n'est qu'une première étape, elle n'en est pas moins porteuse de sens et mérite d'être assimilée. C'est un pas de plus vers la réponse à la question "Qu'est-ce qu'un fluide?", question qui, sans hanter nos nuits, nous servira de fil directeur lorsque nous aborderons les grandes transformations
Principe de correspondance
Munis de notre loi de comportement nous pouvons maintenant, comme nous l'avons fait en élasticité, formuler puis tenter de résoudre un problème de viscoélasticité.
La résolution d'un tel problème est souvent beaucoup plus facile qu'on aurait pu le craindre : on remarque en effet que, formulée en transformée de Laplace-Carson, la loi de la viscoélasticité linéaire est formellement une simple loi élastique, certes paramétrée par p mais peu importe.
C'est le fameux
Principe de correspondance.
Si on connaît la solution d'un problème élastique, on obtiendra la solution du problème viscoélastique correspondant en écrivant en transformée de Laplace-Carson cette solution élastique.
Il ne « reste alors plus qu'à » revenir à l'original, ce qui peut être très lourd, mais qui pourra se faire relativement simplement dans le cas très usuel d'une fraction rationnelle.
On pourrait également traiter de manière analogue et à partir des modules complexes le problème correspondant à une sollicitation harmonique. On pourrait invoquer un « principe de correspondance harmonique ».
