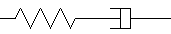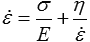Modèles rhéologiques
Vous avez dit Rhéologie ?
Le mot « rhéologie » est entré dans la langue scientifique au début du XXème siècle, en même temps que les modèles rhéologiques qui font l'objet de cette page. Il vient, comme vous vous en doutez, d'une racine grecque, maxime célèbre « τα παντα ρει » – « Tout s'écoule » – traditionnellement attribuée au philosophe grec Héraclite d'Ephèse et en référence au temps (« on ne se baigne jamais dans la même rivière » dit la sagesse populaire), mais le slogan a sans vergogne été détourné par les premiers rhéologues pour parler de la matière. Et c'est ainsi qu'est né le terme rhéologie (on m'a également raconté que la confusion fréquente avec théologie ne déplaisait pas à Marcus Reiner, l'un des pères de la discipline, malicieux dans sa culture hébraïque).
Tout matériau s'écoule, à condition d'attendre suffisamment longtemps, voilà qui ne doit plus vous surprendre maintenant (<) , mais − nous l'avons déjà dit − on se heurte alors à un obstacle majeur et à une limitation essentielle de ce cours : nous nous limiterons aux petites perturbations, alors que si la matière s'écoule (comportement fluide) les déformations peuvent devenir très grandes (et effectivement nous verrons souvent la déformation ε tendre vers l'infini). Un cours de rhéologie n'a donc de sens que dans un contexte de grandes transformations. Et pourtant la plupart des Cours de Comportement des Matériaux (Solides, précise-t-on parfois pour atténuer cette incohérence) se situent dans ce cadre limité. Il y a pour cela deux raisons :
D'un point de vue pratique, la vie est courte et à nos échelles humaines la matière ne s'écoule que modestement (imaginez un peu la technologie d'un monde qui ignorerait la matière solide, un joli thème de Science-Fiction ; je ne me souviens pas l'avoir vu abordé dans la littérature, si vous avez un contre-exemple faites-moi signe !). Cette approximation est donc très largement suffisante pour nombre d'applications.
D'un point de vue théorique, la plupart des concepts et modèles que nous développerons dans la suite resteront largement valables dans le cas général. Toutefois leur mise en oeuvre exigera le formalisme des grandes transformations, formalisme qui reste un peu lourd – beaucoup moins lourd toutefois qu'on ne le pense habituellement. Ce formalisme fera l'objet du cours Grandes Transformations, et nous verrons alors comment étendre les modèles que nous présentons ici. Une bonne compréhension des modèles HPP est à mon avis un préalable indispensable à l'étude de la rhéologie en grandes transformations.
C'est donc dans ce cadre que nous nous plaçons ici.
Les modèles rhéologiques
Les modèles rhéologiques sont des modèles de comportement monodimensionnels simples. Ils sont certes anciens et limités
- par le contexte petites déformations déjà évoqué,
- par leur « simplicité », encore que..., nous y reviendrons,
- par leur caractère monodimensionnel,
et parfois considérés avec une nuance de mépris – Gardez-vous en bien. Correctement interprétés (et ce sera dans ce cours notre fil directeur) ils sont à la racine de toute la Mécanique des Matériaux moderne. Le temps que vous passerez à bien comprendre et sentir leur comportement ne sera pas perdu, et je vous invite fortement à ne pas faire l'impasse sur cette étape.
Modèles élémentaires
Pour l'essentiel ces modèles s'obtiennent par assemblage de modèles élémentaires. Traditionnellement on utilise trois modèles élémentaires.
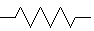Le ressort (élastique) a comme loi de comportement (monodimensionnelle, donc relation entre une contrainte σ et une déformation ε)σ = E ε
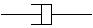L'amortisseur (visqueux) relation contrainte - vitesse de déformationσ = η
Le patin (plastique) ou 
caractérisé par la relation σ - représentée ci-dessous.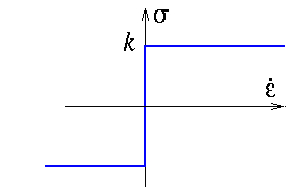
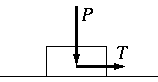Ce dernier modèle est analogue au comportement d'un patin posé sur un plan, soumis à l'action d'une force horizontale T et avec un frottement coulombien. On aura en effet
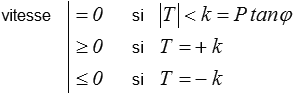
où φ est l'angle de frottement.
Une première démarche de généralisation pourra être d'élargir la bibliothèque de base en introduisant d'autres modèles élémentaires. On utilise par exemple fréquemment (attention toutefois les pictogrammes utilisés sont ici mes conventions personnelles, rien d'universel)
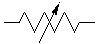ou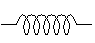 
Le ressort non-linéaire σ = σ (ε) fonction non-linéaire.
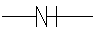Le modèle de Norton-Hoff σ = A m
Retenons une première idée : on pourra construire un modèle complexe par combinaison de modèles élémentaires, et nous consacrerons une part importante de nos efforts à la construction de modèles élémentaires, leur combinaison se faisant ensuite sans grande difficulté (en HPP au moins).
Montage série et parallèle
On utilisera alors pour assembler ces modèles deux règles de combinaison.
Le montage parallèle de deux modèles
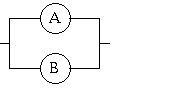ε = ε A = ε B σ = σ A + σ BLe montage série
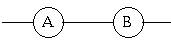ε = ε A + ε B σ = σ A = σ B
mais on peut imaginer des modèles plus complexes, par exemple une combinaison à 5 éléments
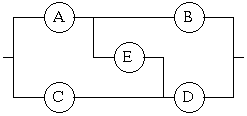ε = ε A + ε B = ε C + ε D = ε A + ε E + ε D
σ = σ A + σ C = σ B + σ E + σ C = σ B + σ D
On parle parfois de modèles géphyroïdes (de γεφυρα = pont). Présentent-ils un intérêt autre qu'exotique ? Pas vraiment, mais cela mérite toutefois d'être examiné d'un peu plus près, nous y reviendrons à l'occasion.
Modèles viscoélastiques
Si nous combinons ressorts et amortisseurs nous pouvons, par exemple, construire avec deux éléments
puis avec trois éléments
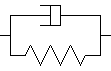
le modèle de Poynting
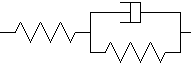
le modèle de Zener
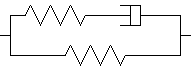
En fait, nous montrerons plus loin que ces deux modèles ne sont que deux représentations différentes du même modèle.
le modèle de Jeffreys
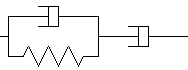ou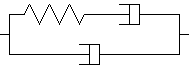 
Citons aussi le populaire modèle de Burgers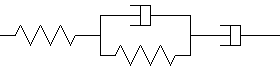 
et ainsi de suite. Tous ces modèles ont comme propriété essentielle d'être linéaires. Nous y reviendrons dans le chapitre viscoélasticité linéaire (>).
Modèles élasto-plastiques
Ce sont les modèles obtenus par montage de ressorts et de patins. On obtiendra alors (comme pour les deux composants élémentaires) un comportement indépendant des vitesses (<).
Dans la suite nous utiliserons les mots « plastique » ou « plasticité » pour évoquer un comportement indépendant des vitesses. Dans le cas contraire nous parlerons de viscoplasticité. Cette convention de terminologie est assez largement – mais non universellement – acceptée.
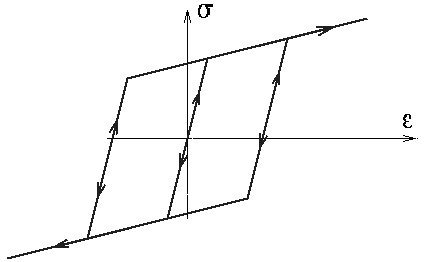
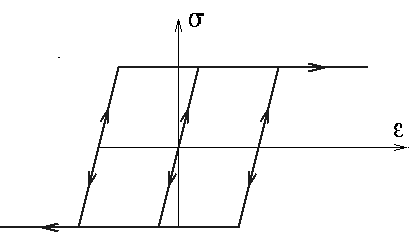Le modèle de base est le modèle que nous appellerons plus tard élasto-parfaitement plastique
Son comportement est décrit par la courbe ci-dessus : comportement élastique au départ tant que | σ | < k , avec écoulement plastique dès que l'on atteint le seuil ≥ 0 si σ = +k , retour élastique si on diminue la contrainte, etc...
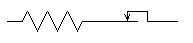
On utilise souvent le modèle de Prager.
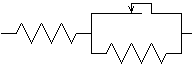
C'est le modèle le plus simple pour la description de la plasticité cyclique.
Modèles élasto-viscoplastiques
Les modèles viscoplastiques s'obtiennent par combinaison de patins et d'amortisseurs, et on se convainc assez facilement que cela revient à un amortisseur non linéaire, c'est-à-dire à une relation non linéaire entre σ et . Dans la pratique on rencontrera souvent le modèle de Bingham
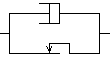σ = k sgn() + η
et nous en arrivons aux modèles élasto-viscoplastiques combinant les trois éléments. Citons par exemple
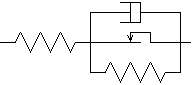
Son nom officiel est « modèle élasto-viscoplastique de Bingham-Perzyna avec écrouissage cinématique linéaire » (ouf ! Rassurez-vous, nous expliciterons plus tard). Ce modèle est parfois utilisé pour le comportement des métaux à haute température, par exemple pour le calcul des aubes de turbines dans un turbo-réacteur.