Interprétation thermodynamique
Modèles élémentaires
Le comportement élastique est conservatif et ne dissipe pas d'énergie. Partant du bilan fondamental (<) , on écrira donc naturellement en situation uniaxiale
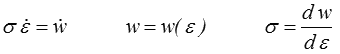
Pour le ressort linéaire
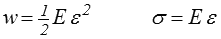
De même pour un modèle purement dissipatif w = 0 et donc
ø = σ  ≥ 0
≥ 0
et sa loi de comportement donnera naturellement une relation entre la contrainte et la vitesse de déformation. Dans le cas monodimensionnel on peut introduire une fonction Ω( ), primitive de la fonction σ(
), primitive de la fonction σ( ). On écrira donc
). On écrira donc
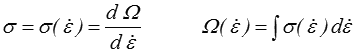
La fonction Ω est appelée potentiel de dissipation.
Pour l'amortisseur la loi est linéaire et le potentiel quadratique
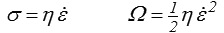
Pour le patin plastique on a de même
σ = k sgn( ) Ω = k |
) Ω = k | |
|
où la fonction sgn( )(sgn = signe) vaut +1 si
)(sgn = signe) vaut +1 si  > 0, −1 si
> 0, −1 si  < 0 et est comprise entre −1 et +1 si
< 0 et est comprise entre −1 et +1 si  = 0 (donc incomplètement déterminée, ce n'est pas une fonction au sens classique du terme, il faudra, pour donner un sens mathématique précis à cette approche, se donner quelque peine. Nous y reviendrons plus loin.)
= 0 (donc incomplètement déterminée, ce n'est pas une fonction au sens classique du terme, il faudra, pour donner un sens mathématique précis à cette approche, se donner quelque peine. Nous y reviendrons plus loin.)
Bingham et Norton-Hoff
 Le modèle de Bingham correspond au montage parallèle d'un ressort et d'un amortisseur, et l'on obtient ainsi directement
Le modèle de Bingham correspond au montage parallèle d'un ressort et d'un amortisseur, et l'on obtient ainsi directement

Le modèle de Norton-Hoff, lui, correspond à une loi puissance
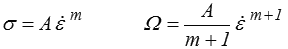
D'un point de vue mathématique, la fonction  m est définie par
m est définie par
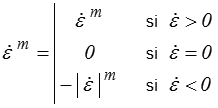
Contrairement à la fonction sgn( ), elle est régulière, dérivable sauf en 0 et biunivoque.
), elle est régulière, dérivable sauf en 0 et biunivoque.
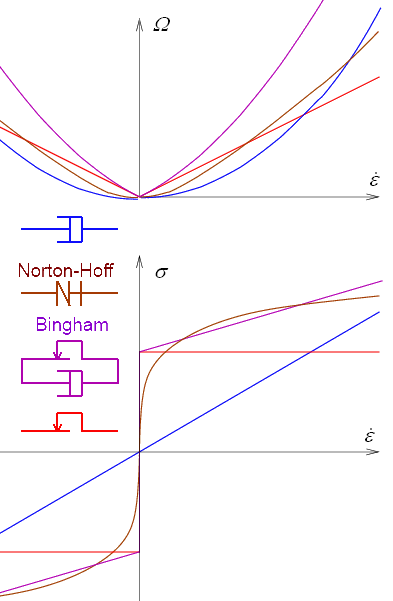
Le graphique ci-contre représente pour les 4 modèles dissipatifs introduits précédemment les deux fonctions donnant σ et Ω en fonction de  .
.
Plus généralement, on pourra traiter de même n'importe quelle loi dissipative, par exemple les lois en sinus hyperbolique souvent rencontrées pour les mécanismes thermiquement activés. Nous imposerons néanmoins à σ d'être fonction croissante de  , ce qui conduit à une fonction Ω(
, ce qui conduit à une fonction Ω( ) convexe.
) convexe.
Nous venons en fait d'introduire ici, dans le cas le plus simple qui puisse exister, la thermodynamique des phénomènes irréversibles (TPI). Le cas visqueux linéaire correspond à la TPI classique (relations d'Onsager) ===> tandis que les autres cas correspondent à la TPI non-linéaire (dissipation normale).
Le modèle élasto-dissipatif
 Ce modèle, important pour les applications, correspond au montage série d'un ressort et d'un élément dissipatif (représenté ici par un carré: amortisseur, patin, modèle de Bingham, de Norton-Hoff,...). Il généralise les modéles de Maxwell (<)
et élasto-parfaitement plastique (<)
.
Ce modèle, important pour les applications, correspond au montage série d'un ressort et d'un élément dissipatif (représenté ici par un carré: amortisseur, patin, modèle de Bingham, de Norton-Hoff,...). Il généralise les modéles de Maxwell (<)
et élasto-parfaitement plastique (<)
.
Dans ce montage le ressort stocke l'énergie tandis que la dissipation provient du seul élément dissipatif. L'énergie et le potentiel de dissipation sont donc respectivement
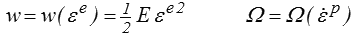
La dissipation s'obtient alors directement par
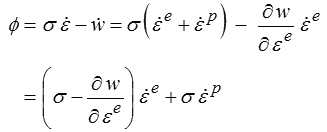
Le premier terme correspond à l'énergie dissipée dans le ressort, il est donc nul et
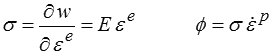
Et on en tire tout naturellement
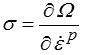
ce qui redonne bien évidemment les équations du modèle rhéologique telles qu'on les aurait obtenues par une approche directe.
La TPI permet de formaliser cette approche selon la démarche suivante :
- On fait une hypothèse sur l'énergie : w = w(εe).
- On en tire les forces et les flux thermodynamiques
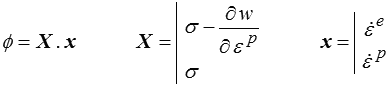
- On fait une hypothèse sur le potentiel de dissipation : Ω(
 p).
p). - On en tire les lois de comportement
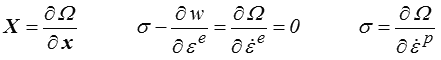
Cette démarche (cadre standard généralisé) est en fait très générale et nous en verrons de nombreuses applications.
Quelques applications
Pour nous familiariser avec cette méthode nous allons maintenant l'appliquer à quelques-uns des modèles rhéologiques classiques.
 Pour décrire le modèle de Prager (<)
il faut rajouter à l'énergie du cas précédent celle du ressort qui se trouve en parallèle du patin
Pour décrire le modèle de Prager (<)
il faut rajouter à l'énergie du cas précédent celle du ressort qui se trouve en parallèle du patin
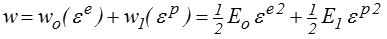
Ceci rajoute un nouveau terme dans la dissipation, qui s'écrira maintenant
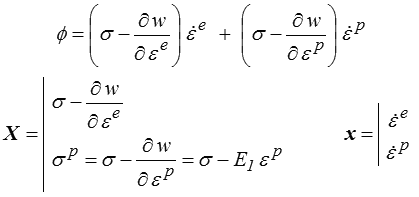
Le potentiel de dissipation pour un modèle de Prager est
Ω( p) = k1 |
p) = k1 |  p |
p |
et l'écriture des lois de la TPI donne maintenant
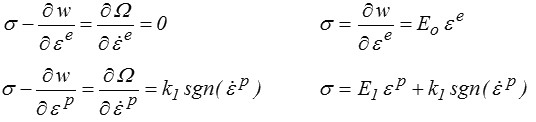
Si l'on veut maintenant remplacer le patin par un amortisseur (modèle de Poynting), par un modèle de Bingham − modèle souvent utilisé pour le fluage des métaux à haute température (<) − il suffit de substituer la forme appropriée du potentiel de dissipation Ω.
Pour le modèle ci-dessous (qui a par exemple été proposé pour modéliser le bitume)
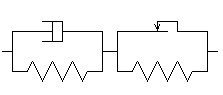
il suffit de rajouter au potentiel de dissipation du patin celui de l'amortisseur
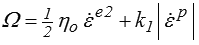
et les lois de dissipation deviennent
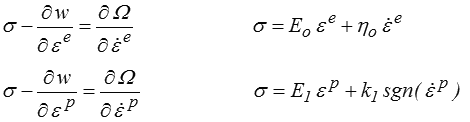
et ainsi de suite ...
