Plasticité standard
Plasticité normale
La plasticité standard (ou normale ou associée, les trois terminologies sont utilisées) correspond au cas où la direction 
est en chaque point de S normale à la surface seuil S.
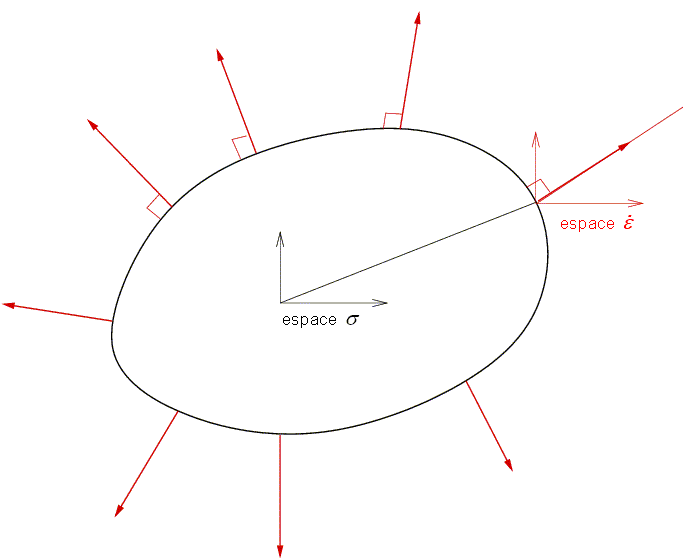
Soit, d'un point de vue mathématique, en se souvenant que le gradient d'une fonction S est normal à ses surfaces isovaleurs, f = Cte
Loi d'écoulement plastique standard.
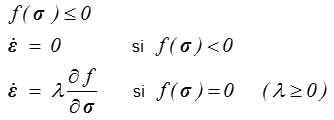
C'est une hypothèse courante donc, mais pas toujours légitime, et on évoquera plus tard des cas où elle n'est pas vérifiée. Toutefois, même dans ces cas, il arrive fréquemment que l'on persiste à la faire, tant elle est commode.
Principe du travail maximal
Cette hypothèse est si importante que l'on a dépensé beaucoup d'efforts à essayer de la « démontrer » à partir d'autres principes. Parmi ceux-ci, le principe du travail maximal joue un rôle particulièrement intéressant : une fois admis le fait que la contrainte σ ne peut pas sortir du domaine C, on détermine la loi d'écoulement plastique, c'est-à-dire les valeurs de associées à une contrainte σ donnée, par
Principe du travail maximal.
σ . ≥ σ* . ∀ σ* ∈ C
Parmi tous les états de contrainte admissibles, la loi d'écoulement maximise le travail.
| On peut aussi écrire ( σ − σ* ) . ≥ 0Vectoriellement cela signifie que, dans l'espace vectoriel de dimension 6 des tenseurs symétriques, le vecteur σ* σ fait un angle aigu avec le vecteur pour tout σ* admissible. |
 |
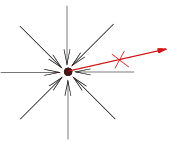
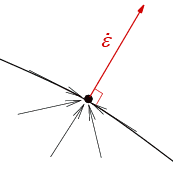
| Si σ* est intérieur à C alors le vecteur σ* σ peut prendre toutes les directions possibles, et le seul vecteur vérifiant la condition est le vecteur nul. |
 |
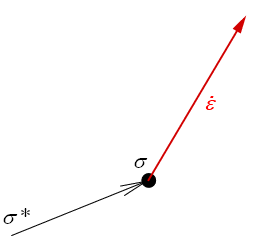
| Si σ* est sur la frontière, alors le vecteur σ* σ vient de l'intérieur de C ou est au mieux tangent à S. La condition montre alors que doit être dirigé selon la normale extérieure à C. |
 |
| On peut même faire bien plus : on remarque tout d'abord que cette condition exige la convexité du domaine C. En effet, si le domaine n'était plus convexe on pourrait trouver, lorsque σ est sur S, un point σ* dans C et tel que le vecteur σ* σ rentre dans C, violant ainsi l'inégalité. |  |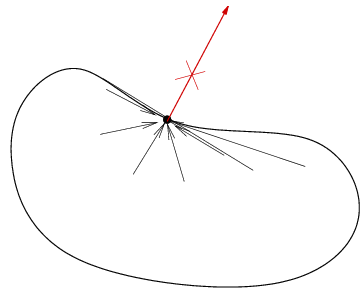
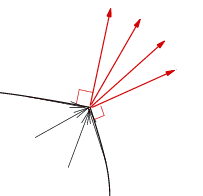
| On peut également prendre ainsi en compte le cas d'une surface seuil présentant un point anguleux, donc pour laquelle on ne saurait définir une fonction seuil f dérivable. La condition du travail maximal montre alors que le vecteur doit être dans le cône des normales (c'est-à-dire le cône limité par toutes les normales à S au point anguleux correspondant). |
 > |
Fonction de dissipation
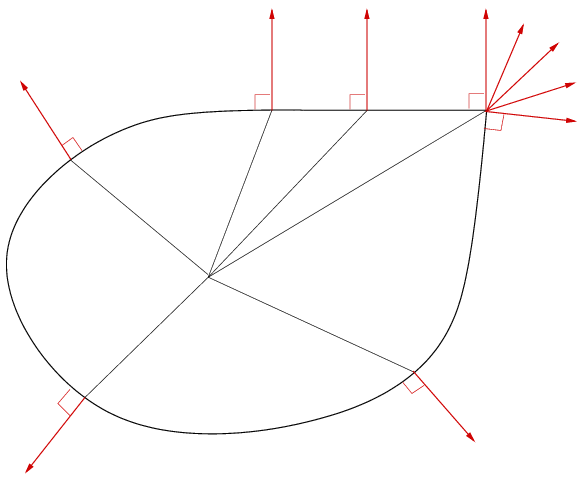
La loi d'écoulement plastique est donc une relation entre un état de contrainte sur le seuil et une direction de vitesse de déformation. C'est toutefois dans ce cadre une relation complexe puisque non univoque, ni dans un sens, ni dans l'autre. Plusieurs directions de vitesses de déformation peuvent correspondre à un seul état de contrainte (cas d'un point anguleux de la surface seuil) et une direction peut correspondre à plusieurs états de contrainte (cas d'une portion plane − rectiligne en 2D − de la surface seuil). On remarque toutefois que dans ce dernier cas le produit scalaire σ . prend, pour tous ces états de contrainte, la même valeur. La dissipation
ø = D() = σ .
sera donc bien une vraie fonction de , c'est la fonction de dissipation.
On peut alors montrer que si cette fonction est différentiable on peut écrire que la contrainte s'obtient par dérivation de cette fonction D. On est donc dans le cadre de la dissipation normale (<) avec un potentiel de dissipation Ω = D
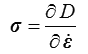
La plasticité standard correspond donc à l'application au cas d'un comportement plastique, c'est-à-dire indépendant des vitesses, de l'hypothèse de dissipation normale.
Il mérite également d'être signalé que, malgré son apparente complexité et son incontestable lourdeur, cette loi d'écoulement plastique est, même dans son cas général, mathématiquement agréable et permet de démontrer des propriétés intéressantes.
Potentiels plastiques
La plasticité standard constitue donc un cadre très général, très commode d'utilisation lorsqu'il existe une fonction seuil, c'est-à-dire dans le cas d'une surface seuil régulière. C'est un peu lourd dans le cas contraire.
Cette situation d'une surface seuil non régulière se rencontre le plus souvent lorsque la plasticité peut résulter de plusieurs mécanismes avec une condition de seuil pour chacun d'entre eux. Le domaine plastique est alors l'intersection des domaines associés à chacun de ces mécanismes. Et ceci entraîne bien évidemment des points anguleux à l'intersection des surfaces seuils associées, c'est-à-dire lorsque plusieurs mécanismes sont actifs. La loi d'évolution standard s'écrit alors tout naturellement
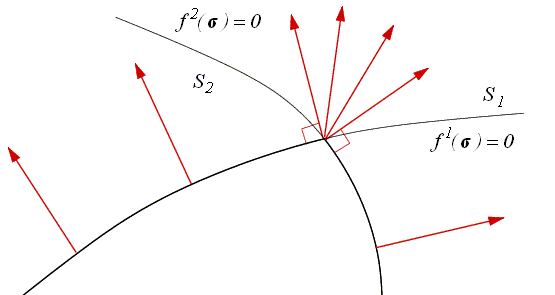
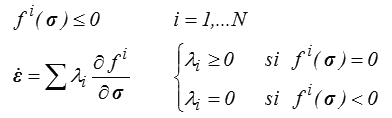
On parle de potentiels plastiques multiples en considérant que la fonction seuil f i est associée au « potentiel plastique » permettant d'écrire la loi d'évolution. C'est pour cette raison que la plasticité standard est également appelée plasticité associée.
Plasticité non associée
Nous avons déjà signalé que, bien que très couramment faite, cette hypothèse n'est pas toujours légitime. La loi d'écoulement plastique fait alors intervenir, outre la fonction seuil f, une fonction tensorielle g donnant la direction de l'écoulement plastique. Pour ce faire, il est naturel et courant de postuler que cette fonction dérive d'un potentiel scalaire g(σ). On généralisera donc la loi standard au cas non standard en écrivant
Loi d'écoulement plastique non standard.
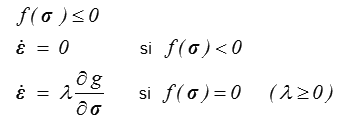
avec deux fonctions scalaires différentes : la fonction seuil f et le potentiel plastique g. On parle alors de plasticité non associée ; le potentiel plastique n'est plus associé à la fonction seuil.
On peut bien évidemment généraliser sans difficulté au cas multi-mécanismes décrit plus haut. A titre d'exemple on utilise souvent en mécanique des sols des modèles à deux mécanismes, l'un associé, l'autre non associé.