Dissipativité normale
La TPI non linéaire
La TPI classique (<) correspond à un modèle linéaire et, comme le montrent les exemples évoqués plus haut, elle participe au patrimoine commun de la physique du XXème siècle. Ses applications à la mécanique des matériaux restent toutefois limitées, quoique parfois importantes notamment en viscoélasticité. Le comportement des matériaux sera en général très fortement non-linéaire, et nous aurons besoin d'une extension de la TPI au cas non linéaire. Cela semble simple et l'extension que nous allons présenter peut paraître bien naturelle. Elle ne l'est pas, et il a fallu près d'un demi-siècle de tâtonnements pour y parvenir, avant d'arriver, vers 1975-1980, à la réponse finale.
L'idée de départ est très simple : si l'écriture matricielle des relations d'Onsager est par essence limitée au cas linéaire, l'écriture dérivée d'un potentiel de dissipation ne l'est par contre pas. La TPI non linéaire sera donc basée sur l'introduction d'un potentiel de dissipation Ω(x) ou ω(X) permettant d'écrire
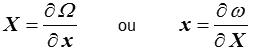
avec un potentiel de dissipation Ω(x) ou ω(X) non nécessairement quadratique et auquel nous n'imposerons que d'être une fonction convexe, hypothèse mathématique essentielle qui assure un développement rigoureux et harmonieux de tout ce qui va suivre. On remarque que, dans le cas d'un modèle dissipatif 1D, ceci correspond simplement au fait que σ = X est fonction croissante du flux x = 
.
Transformation de Legendre
Une loi de TPI non linéaire fait donc intervenir l'un ou l'autre des deux potentiels de dissipation Ω(x) ou ω(X). En fait, si l'on connaît l'un, on peut déterminer l'autre par une transformation de Legendre.
Partant par exemple de Ω(x), la relation
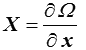
donne la force X en fonction du flux x. L'inversion de cette relation donne x en fonction de X. On détermine ensuite la fonction ω(X) par
ω(X) = X . x − Ω(x) ( x = x(X) )
En effet, en différentiant cette relation il vient
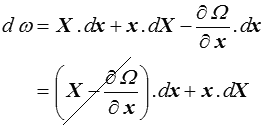
qui montre bien que x est la dérivée de ω par rapport à X. De même
Ω(x) = X . x − ω(X) ( X = X(x) )
C'est la transformée de Legendre .
Dans le cas linéaire par exemple,
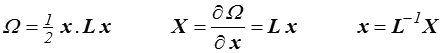
La transformée de Legendre sera donc
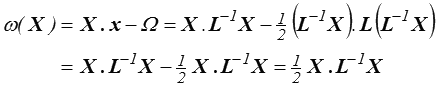
c'est-à-dire le résultat obtenu plus haut avec l = L−1.
Le lecteur aura peut-être reconnu dans cette définition et ce raisonnement ce qui, en thermodynamique classique, permet de définir l'enthalpie libre (ou l'enthalpie ou l'énergie libre) à partir de l'énergie interne ou bien, en mécanique analytique, le hamiltonien en fonction du lagrangien s(<) .
Pour être légitime, notre raisonnement exige certaines conditions de régularité (et notamment que l'on puisse inverser la relation X(x) pour calculer x en fonction de X ). C'est justement ici qu'intervient la convexité de la fonction Ω qui permet de justifier et de généraliser ces définitions. Pour être plus précis, il faudra donc rentrer un peu plus en détail dans la théorie mathématique des fonctions convexes.
Quelques exemples monodimensionnels
Dans le cas monodimensionnel d'un modèle purement dissipatif, X = σ et x = . Que deviennent dans ce cas les modèles élémentaires ?
Pour un amortisseur
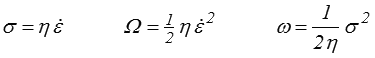
Pour un modèle de Norton-Hoff
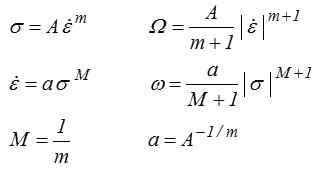
Pour un modèle de Bingham
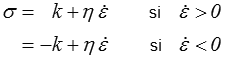
d'où l'on tire directement
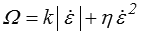
Inversement on peut écrire
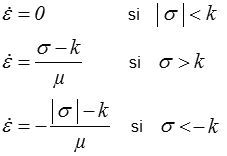
et le potentiel s'écrira
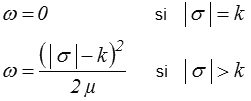
que l'on peut réécrire
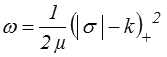
où a+ représente la partie positive de a ( a+ = a si a ≥ 0, 0 si a ≤ 0 ).
Pour un patin plastique
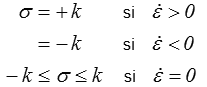
et donc Ω = k | |
mais on ne peut pas calculer en fonction de σ.
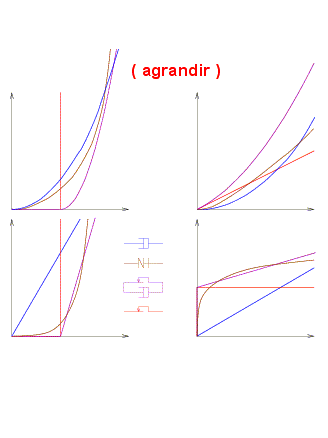
La représentation graphique des 4 fonctions σ(), Ω(), (σ) et ω(σ) illustre ces relations. On y constate de visu que la singularité du cas plastique était prévisible.
Fonctions et potentiels de dissipation
Dans le cas linéaire, nous avons déjà constaté que les deux potentiels de dissipation étaient reliés à la dissipation ø = X . x. On retrouvera cette propriété sitôt que la loi de dissipation sera homogène, c'est-à-dire lorsque l'on pourra écrire pout tout λ positif
X( λ x ) = λm X( x ) Ω( λ x) = λm+1Ω( x )
(la fonction Ω est positivement homogène de degré m+1). On vérifie alors que la fonction x(X) est, elle, positivement homogène de degré M = 1/m
x( λ X ) = λM x( X ) ω( λ X ) = λM+1ω( X )
On en tire directement par la relation d'Euler
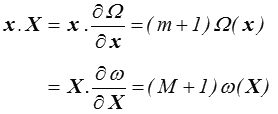
En introduisant la « fonction de dissipation » ø = X . x, fonction de x ou de X on peut donc écrire
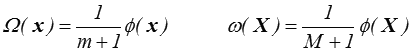
Dans le cas linéaire, m = M = 1, et on retrouve le potentiel de dissipation égal à la moitié de la dissipation. Dans le cas plastique m = 0, et le potentiel de dissipation est égal à la fonction de dissipation, classiquement notée dans ce cas D(x)
Ω(x) = D(x) = x . X
Par contre M = 1/0 ! de sorte que l'on ne sait pas expliciter la fonction ω(X).
Ces résultats sont certes très sympathiques, mais limités au cas d'une fonction homogène. On vérifie par exemple que l'on ne peut rien écrire de tel pour un modèle de Bingham, et il faut accepter le fait que, contrairement à la fonction de dissipation, le potentiel de dissipation est un outil de formulation sans signification physique directe.