Loi d'écoulement plastique
La loi de comportement
Le modéle de base de la plasticité est le patin plastique (<). Etendu au cas tri-dimensionnel, le modèle plastique correspondra donc à une loi dissipative (σ fonction de 
) et indépendante des vitesses. La fonction σ() doit donc vérifier la condition suivante
σ ( λ ) = σ ( ) ∀ λ > 0
En effet, la contrainte doit rester inchangée si l'on change la vitesse du processus, ce qui revient bien à multiplier la vitesse par un scalaire positif quelconque. On dit que la fonction σ est positivement homogène de degré 0 (w)
.
Toute la structure de la plasticité, aussi complexe et mystèrieuse qu'elle puisse paraître, résulte en fait de cette propriété.
On remarquera aussi que cette formulation est en fait tout à fait naturelle, et, si l'on pouvait s'arrêter là et se limiter à cette écriture, la plasticité serait toute simple.
Seuil de plasticité
Nous avons déjà insisté sur le fait que la loi de comportement permettait de calculer les contraintes en fonction de la déformation ou vice versa. Or dans les applications de la plasticité on verra plus loin que cette écriture inverse, déformation en fonction des contraintes, est en général plus utile.
Il suffit donc d'inverser la loi de comportement. Mais encore faut-il pouvoir de faire, et en plasticité c'est impossible !
D'un point de vue géométrique la loi plastique est une application de l'espace des vitesses de déformation dans celui des contraintes (tous deux espaces vectoriels de dimension 6). Les représentations géométriques que nous allons présenter seront évidemment bidimensionnelles; elles seront en général fidèles, mais il importe néanmoins de conserver cette nuance à l'esprit, elle peut parfois être importante.
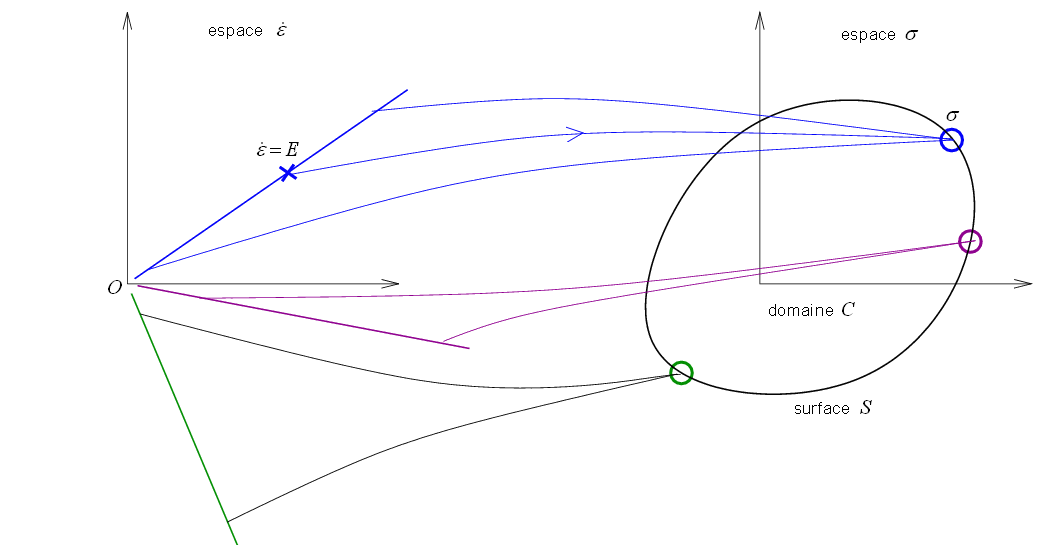
La propriété d'indépendance des vitesses se traduit par le fait que si σ est l'image de E = 
, ce sera aussi l'image de tous les λ avec λ positif, donc de toute la demi-droite OE (ouverte, c'est-à-dire origine non comprise). Lorsque cette demi-droite tourne autour de l'origine, le point correspondant dans l'espace des contraintes décrit une surface fermée S (techniquement une hypersurface de dimension 5 dans l'espace des contraintes, ce qui, ici en deux dimensions, se réduit à une courbe).
Géométriquement cette surface S est l'image par la loi de comportement σ() de tout l'espace moins l'origine. Et l'origine alors? La seule possibilité raisonnable est de supposer que l'image de l'origine sera le domaine C limité par S. Nous sommes ici guidés par le cas monodimensionnel où C est le segment [−k ,+k] limité par les deux points −k et +k. Nous sommes également guidés par le cas des matériaux standard qui sera présenté plus loin, mais je n'ai pas, dans le cas général, de justification plus convaincante que l'impossibilité de faire autrement (Ce n'est déjà pas si mal!).
D'un point de vue mécanique, ceci montre que l'écoulement plastique ne peut se produire que si la contrainte se trouve sur cette surface S, appelée surface seuil, tandis que le domaine C limité par S est habituellement nommé domaine de plasticité ou domaine élastique.
Loi d'écoulement
L'écoulement plastique ne peut donc se produire que pour un état de contrainte σ situé sur la surface seuil. Dans ce cas il lui correspondra dans l'espace toute une demi-droite (que nous supposons pour l'instant unique, il peut arriver que plusieurs demi-droites correspondent au même état de contraintes. Nous en verrons plus loin quelques exemples.)
La loi d'écoulement exprime donc une relation entre un tenseur des contraintes situé sur la surface seuil et une direction dans l'espace des vitesses de déformation. On écrira alors
= λ g(σ) ∀ λ ≥ 0
où le scalaire λ traditionnellement appelé multiplicateur plastique peut prendre une valeur quelconque − non déterminée en tout cas par la loi de comportement. Nous verrons plus loin comment le calculer pour fermer le problème. La structure générale d'une loi d'écoulement plastique est donc
Loi d'écoulement plastique.
Insistons à nouveau sur le fait que cette structure − apparemment compliquée − ne sort pas de l'imagination délirante d'un savant fou : c'est en fait la conséquence naturelle et inéluctable du caractère indépendant des vitesses.
Cas d'une fonction seuil
Sauf mention explicite du contraire, nous nous limiterons désormais au cas où le domaine C et sa surface S sont suffisamment réguliers pour que l'on puisse les définir par une fonction seuil f(σ) nulle sur S et négative à l'intérieur de C (défini donc par la condition f ≤ 0 )
La loi d'écoulement plastique s'écrit alors :
Loi d'écoulement plastique.
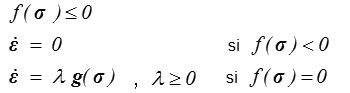
Géométriquement on représentera cette loi par le graphique ci-dessous - contrainte en noir, vitesse de déformation en rouge en se souvenant que seule sa direction est connue
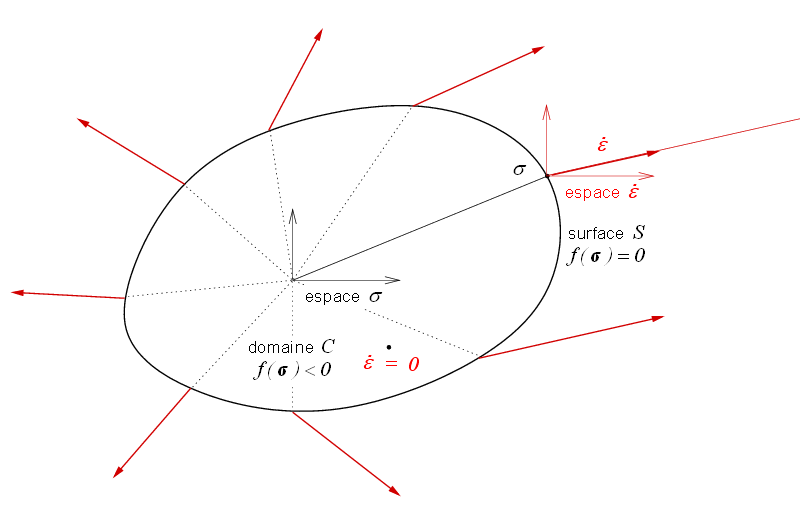
On remarquera enfin que pour définir complètement cette loi il faut connaître deux fonctions : une fonction scalaire f définissant le seuil et une fonction tensorielle g définissant en chaque point de la surface seuil la direction de .