Le modèle de Maxwell
C'est un modèle des plus simples mais néanmoins très riche et important. Nous le retrouverons d'ailleurs de manière tout aussi essentielle en grandes transformations.
Définition
C'est le montage série d'un ressort et d'un amortisseur, et on procède, pour écrire son comportement, comme nous l'avons fait pour le modèle de Kelvin
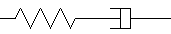
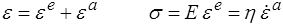
(a comme amortisseur ou anélastique. On utilise aussi souvent la notation ε p au lieu de ε a. Nous verrons bientôt pourquoi). On en tire directement après dérivation par rapport au temps
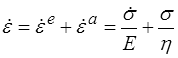
Comportement en fluage
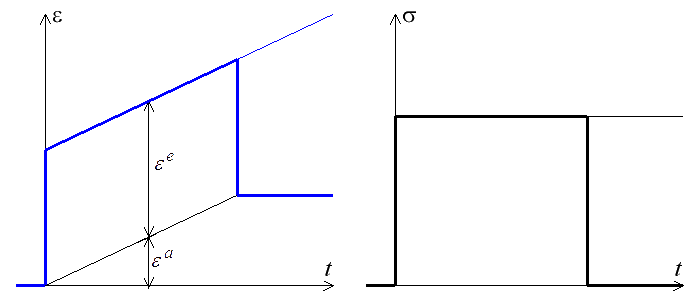
Le comportement en fluage, et plus généralement sous contrainte imposée, est très simple : il suffit d'évaluer les deux allongements ε e et ε a puis de faire la somme. Si la contrainte appliquée est constante σo il vaut
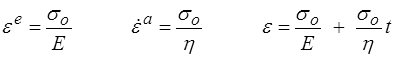
De même, si à l'instant to on annule la contrainte appliquée (créneau de contrainte), le ressort reprend sa longueur initiale (ε e= 0 ) tandis que l'amortisseur se fige à sa position à l'instant to, ε a = σo to / η. Il subsiste, après relâchement de la contrainte, une déformation permanente résiduelle. Ceci explique la notation ε p (p comme permanente) au lieu de ε a. On notera l'analogie (non fortuite) avec la notation introduite pour la plasticité des métaux (<).
Comportement en relaxation
Contrairement à ce qui se passait pour le modèle de Kelvin, un saut de contrainte correspond à un saut de déformation (seul le ressort agit), et on peut, dans un essai de relaxation, (en théorie bien sûr, en pratique c'est une autre histoire) imposer instantanément la déformation εo avec la contrainte σ = E εo.

Il faut ensuite, pour obtenir la réponse en contrainte, intégrer l'équation différentielle
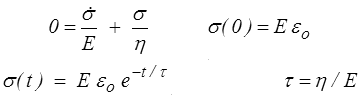
L'interprétation physique est claire : la déformation imposée est initialement supportée par le ressort qui, en s'allongeant, engendre une contrainte. Cette contrainte met en action l'amortisseur qui progressivement assume une part de plus en plus importante de la déformation imposée, relâchant d'autant la part du ressort qui progressivement revient à sa longueur initiale.
Le ressort pilote le comportement instantané (temps courts), tandis que c'est l'amortisseur qui contrôle le comportement différé (temps longs).
On vendait jadis dans les drugstores une balle gadget que vous pouviez faire rebondir comme une balle (élastique aux temps courts) mais que, posée et laissée sur une table, vous retrouviez le lendemain étalée en flaque (fluide visqueux aux temps longs). Regardez aussi cette démonstration avec même une recette pour épater vos amis (je n'ai pas testé)
C'est ce comportement qu'idéalise le fluide de Maxwell.
Loi héréditaire
Pour déterminer la contrainte correspondant à une déformation donnée, il faut, pour une histoire de déformation ε(t) donnée, intégrer une équation différentielle. Comment faire ? C'est une équation différentielle linéaire non homogène (avec second membre). On utilise la méthode dite de variation des constantes − on l'utilise finalement assez peu, et vous l'avez peut-être oubliée : on intègre déjà l'équation homogène (sans second membre)
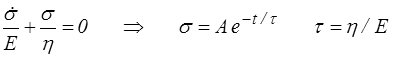
et on cherche ensuite la solution de l'équation non homogène sous la forme
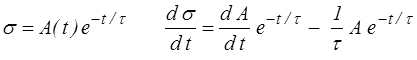
de sorte que l'équation différentielle devient
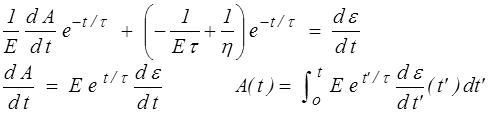
en supposant, comme on le fait habituellement, que le modèle n'a été sollicité qu'à partir de l'instant t = 0 ( σ = ε = 0 pour t ≤ 0 ). On peut d'ailleurs remplacer la borne inférieure par − ∞ , ce que nous ferons désormais. On obtient finalement
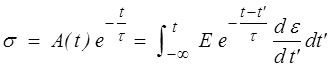
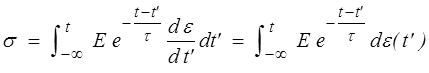
Cette forme suppose, comme l'équation différentielle qu'elle intègre, que la fonction ε(t) est dérivable, mais on peut montrer qu'elle reste valable si ε subit des sauts (discontinuités de première espèce), l'intégrale devenant alors une intégrale de Stieltjes. Ne vous préoccupez pas de cela, nous verrons plus loin un formalisme mathématique bien mieux adapté.
Il y aurait beaucoup à dire sur cette écriture, nous y reviendrons dans un cadre plus général. Remarquons simplement que nous rencontrons, comme nous l'avions annoncé (<) , une dépendance par rapport à l'histoire de déformation (mémoire du matériau). On a dans ce cas construit sous forme explicite la fonctionnelle de réponse.
