Diversité des comportements
Nous connaissons maintenant notre « produit » final mais il nous faut aussi nous intéresser au « marché », c'est à dire à notre champ d'investigation, le comportement réel des Matériaux et aux données expérimentales dont nous pouvons ou devons disposer.
Les essais mécaniques
Nous les avons déjà largement évoqués dans le cours d'introduction à la MMC (<) mais nous avions alors occulté un aspect important sur lequel nous devons maintenant revenir : pour un matériau élastique la loi de comportement reliait le tenseur des contraintes σ et des déformations ε. Il fallait donc, dans un essai, pouvoir imposer l'un et mesurer l'autre, et cela nous avait déjà causé bien du souci (rappelons que l'on ne sait pas mesurer les contraintes et a fortiori encore moins les imposer).
Mais nous savons aussi maintenant que la loi de comportement (<) donne la contrainte en fonction de l'histoire de déformation ou la déformation en fonction de l'histoire de contrainte, et il nous faut maintenant prendre en compte cette notion d'histoire. Il ne suffit pas de préciser quelle déformation on impose, il faut aussi savoir comment on l'impose (brutalement ou progressivement ? directement ou avec des retours en arrière ?...).
Nous limiterons l'essentiel de la discussion à une sollicitation simple, de traction simple par exemple, car cet essai reste, en mécanique des matériaux, l'essai le plus courant. Cet aspect devra toutefois être pris en compte de manière plus générale
Comportement indépendant des vitesses
L'essai le plus naturel consiste à augmenter progressivement (charge monotone) la contrainte ou la déformation, selon ce que l'on a choisi d'imposer. (En fait, la technologie de réalisation de l'essai conduit plutôt à imposer l'une ou l'autre de ces variables, mais un asservissement permet en général de contrôler l'autre si on le souhaite, c'est donc bien notre choix, et ce choix n'est souvent pas indifférent). Le résultat de l'essai est alors une courbe contrainte-déformation. Encore faut-il toutefois préciser les conditions d'essai, c'est-à-dire en l'occurrence la vitesse de sollicitation.
Pour certains matériaux et sous certaines conditions on peut toutefois – en première approximation et en restant dans les limites raisonnables – constater que la courbe obtenue ne dépend pas de la vitesse de sollicitation. On parle alors d'un comportement indépendant des vitesses (rate-independent, en anglais).
C'est en particulier le cas pour les matériaux métalliques à température ambiante, et c'est dans ce cadre que l'on se place très souvent pour décrire leur comportement. La normalisation de l'essai de traction laisse pour cette vitesse une large plage de valeurs, alors qu'elle est pourtant très pointilleuse sur d'autres points, par exemple sur la géométrie de l'éprouvette et en particulier le rapport longueur/diamètre (Pourquoi ?).Bonne question. Normalement la définition de la contrainte (force/section) et de l'allongement (variation relative de longueur) permet justement de s'affranchir de cette géométrie. Je vous laisse méditer cette question. Nous y reviendrons plus tard.
En termes géométriques cela signifie que pour connaître la contrainte il faut connaître, dans l'espace des déformations, la trajectoire décrivant la sollicitation, mais non sa loi horaire, c'est-à-dire la vitesse à laquelle elle est parcourue. Lorsqu'elle est justifiée c'est une approximation très intéressante car elle permet de représenter le comportement dans le plan ( σ − ε ) en oubliant la variable temps.
Quelques exemples
Comme indiqué plus haut l'exemple le plus classique est celui des matériaux métalliques à température ambiante (===>) , mais on utilisera ce type de modèle pour bien d'autres matériaux.
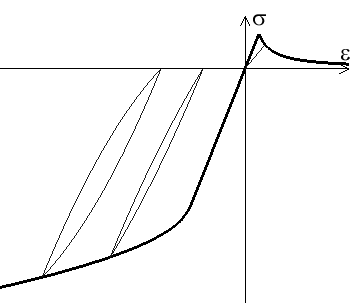
C'est par exemple le cas du béton qui présente, en compression, un comportement analogue quoique la déformation « plastique » (c'est-à-dire conduisant à une déformation résiduelle après relâchement de contrainte) s'accompagne d'une dégradation des caractéristiques élastiques et d'une hystérésis importante. Le comportement en traction conduit au contraire à une rupture brutale sous une contrainte faible (de l'ordre de 10% de la limite élastique en compression). Dans la pratique, différentes techniques de construction (béton armé, béton précontraint, structure en arc) permettent d'éviter les contraintes de traction que le béton supporte très mal. Le comportement des roches est similaire.
Le cas des sols (sable, argile,...) et plus généralement des matériaux peu ou pas cohérents (poudres) présentent des difficultés spécifiques (influence de la pression de confinement, utilisation des essais oedométrique (<) et "triaxial" (<) ,...) .
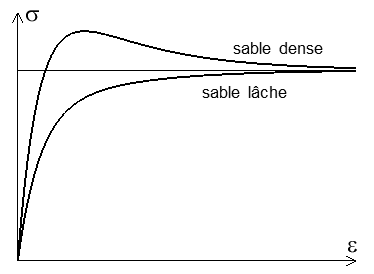
Nous avons par exemple représenté ci-contre le comportement d'un sable dans un essai triaxial. On note une très grande importance de l'état initial de compaction. Ce comportement complexe pourra néanmoins être considéré comme indépendant des vitesses.
Plus généralement, cette approximation d'un comportement indépendant des vitesses sera très souvent utilisée, au moins en première approximation, car elle simplifie grandement la description du comportement et également sa modélisation .Il conviendra néanmoins d'écarter au préalable quelques difficultés techniques spécifiques à cette approximation (>).
Fluage
La première manifestation de la dépendance des vitesses est la constatation que la courbe de traction (ou plus généralement la réponse à un essai de charge monotone) dépend de la vitesse de sollicitation. Il est alors intéressant d'utiliser d'autres essais plus simples et prenant explicitement en compte la variable temps.
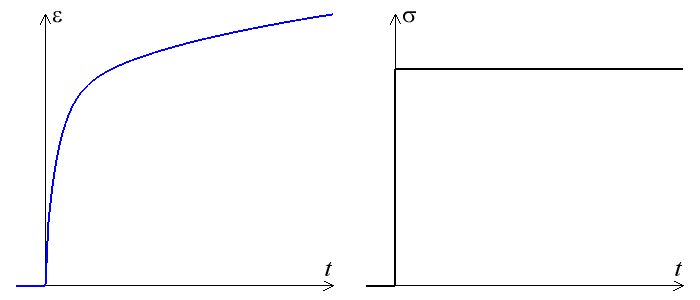L'essai de fluage consiste à imposer à une éprouvette initialement au repos un échelon de contrainte
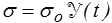
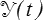est la fonction de Heaviside (échelon unité)
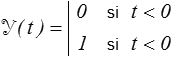
Si le comportement est indépendant des vitesses, il en résulte simplement et immédiatement une déformation ε = εo ( σo ) fonction de σo mais qui ensuite n'évolue plus.
Pour un comportement dépendant des vitesses au contraire, la déformation augmentera progressivement au cours du temps.Plus généralement, le phénomène de fluage (creep, en anglais) correspond à l'augmentation de la déformation ( 
> 0 ) sous contrainte constante.
D'un point de vue expérimental, l'essai de fluage est assez facile à réaliser : il suffit d'appliquer une force constante (nous nous limitons, rappelons-le, aux petites perturbations, et négligeons donc les variations de la section S de l'éprouvette), par exemple à l'aide d'un poids.
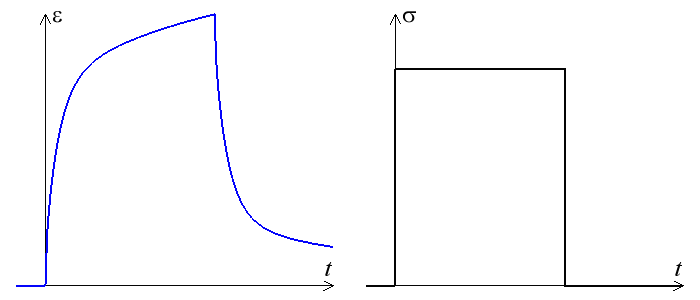
Cet essai est souvent poursuivi en annulant au bout d'un certain temps T la contrainte appliquée (créneau de contrainte) et en observant la recouvrance, c'est-à-dire le retour progressif (partiel ou complet) vers l'état initial (décroissance de la déformation).
On peut s'interroger (et nous le ferons souvent dans la suite) sur ce qui se passe pour des temps très courts (comportement instantané) ou pour des temps très longs (comportement différé). Pour intéressants qu'ils soient, ces débats sont purement théoriques car expérimentalement inaccessibles : on ne peut pas réaliser un chargement instantané, il y faudra toujours un certain temps et même si l'on peut aller très vite, les effets dynamiques viendront alors perturber l'essai.
Pour les temps très longs, la vie humaine est courte (attention des essais de fluage peuvent être menés sur plusieurs années) et d'autre part l'essai finira toujours par conduire à la rupture. Ces essais de fluage à rupture sont en fait couramment menés, et on distingue traditionnellement trois zones.
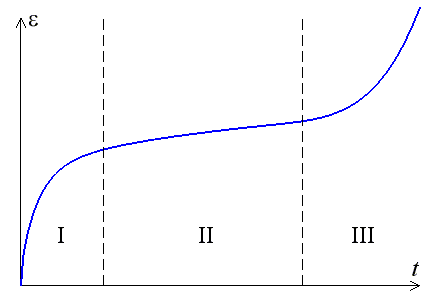
- zone I : fluage primaire. Elle correspond à une vitesse de déformation positive mais décroissante jusqu'à atteindre
- zone II : fluage secondaire ou fluage stationnaire. Elle correspond à une stabilisation de la vitesse de déformation fonction croissante de la contrainte appliquée ;
- zone III : fluage tertiaire. Elle correspond à la dégradation du matériau, qui conduit à une accélération de la déformation, puis finalement à la rupture.
Relaxation
Le phénomène de relaxation (des contraintes) correspond à la décroissance de la contrainte nécessaire pour maintenir une déformation constante.
L'essai de relaxation, symétrique de l'essai de fluage, consiste à appliquer un échelon de déformation. Le début de l'essai, c'est-à-dire la montée en déformation pose encore plus de problème qu'en fluage car il est plus difficile – voire impossible – d'imposer une déformation très rapide, mais on observe ensuite une décroissance régulière de la contrainte.
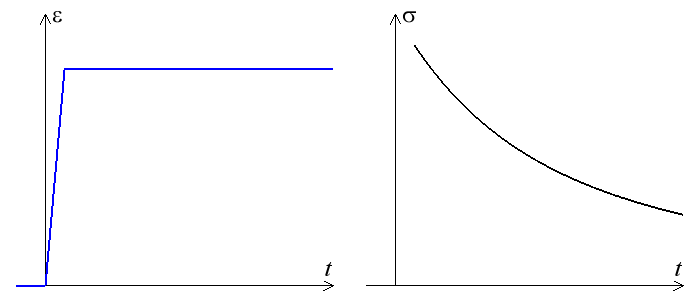
Comme pour le fluage on peut s'interroger sur ce que deviennent ces contraintes lorsque t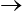 
∞ (comportement différé). La contrainte diminuera-t-elle jusqu'à zéro ou subsistera-t-il une contrainte σo ? Question importante bien sûr. Mais là encore l'expérience, nécessairement limitée dans le temps, ne permettra en général pas de trancher. On ne sait caractériser le comportement que sur des échelles de temps compatibles avec nos moyens expérimentaux, donc limités tant pour les temps courts (comportement instantané) que pour les temps longs (comportement différé).
On notera que, d'un point de vue technologique, cet essai est moins simple à réaliser que l'essai de fluage et qu'il exige une machine d'essai. Les durées d'essai seront donc nécessairement limitées, alors que les essais de fluage peuvent parfois durer plusieurs années.
Essais harmoniques
Sous sollicitations cycliques la dépendance des vitesses induit une dépendance par rapport à la fréquence. Il sera donc intéressant de caractériser directement cette dépendance en réalisant des essais à fréquence imposée. Ces essais sont le plus souvent réalisés sous sollicitations harmoniques. Suivant la technologie d'essai on imposera par exemple une déformation fonction harmonique du temps
ε = εo sin ωt
et on observera la réponse en contrainte. En général ces appareils (viscoélasticimètres) sont équipés d'outils de traitement du signal extrayant de cette réponse une réponse harmonique « équivalente »
σ ≈ σo sin (ωt+δ)
L'essai de viscoélasticimétrie permettra alors de décrire, en fonction de la fréquence de sollicitation f = ω/2π, le rapport d'amplitude σo /εo et l'angle de perte δ. On notera toutefois que ceci n'a de sens précis que si une sollicitation harmonique induit une réponse harmonique. Ce sera parfois vrai – nous y reviendrons (>) – mais pas toujours. Il faudra alors se méfier de ce type de résultat.
On notera également que les résultats de ces essais dépendent fortement (comme d'ailleurs en fluage et relaxation) de la température – qui doit donc être correctement contrôlée.
Essais complexes
Un modèle de comportement doit rendre compte de la réponse du matériau en toutes circonstances. Les essais que nous avons décrits plus haut correspondent à des situations très simples. Ils permettront souvent de proposer et d'identifier un modèle de comportement, mais il sera souvent nécessaire d'avoir recours à des essais impliquant des sollicitations plus complexes. Citons par exemple
- Pour des comportements indépendants des vitesses, des essais cycliques à niveau variable : cyclage en déformation (>)
ou en contrainte (>)
à un niveau (un certain nombre de cycles, ou jusqu'à saturation), puis on recommence en changeant le niveau. Dans le même ordre d'idée, on cherche à reproduire en laboratoire une sollicitation que l'on estime représentative des conditions réelles de sollicitation (souvent mal connues, et au mieux statistiquement). C'est le domaine de la fatigue à programme, domaine important que nous ne traiterons pas.
- Pour un comportement dépendant des vitesses, on réalise souvent des essais de fatigue-fluage : successions de cyclage (fatigue) et de maintien sous contrainte (fluage).
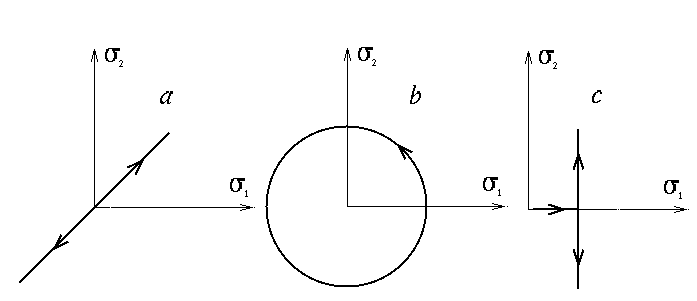
Nous nous sommes ici limités à une sollicitation monoaxiale (traction par exemple). L'éventail des possibilités s'élargit considérablement si l'on passe aux sollicitations multiaxiales. Par exemple, pour un matériau indépendant des vitesses en sollicitation biaxiale (<) ou en traction-torsion (<) , on doit envisager divers types de sollicitations
- sollicitation radiale,
- sollicitation circulaire,
- effet de précharge.
Il est aussi parfois nécessaire de faire varier la température (on parle alors de sollicitations thermomécaniques) et là encore il convient de préciser l'histoire de température, élargissant encore davantage le champ des possibles.
Conclusion provisoire
Nous n'avons fait ici qu'effleurer le sujet, mais le lecteur aura compris, au travers de cette première approche, que la description (caractérisation, classification, modélisation) des comportements est une tâche lourde et qui s'apparente un peu à celle du naturaliste.
« Construire la loi de comportement d'un matériau donné », telle pourrait être la finalité de ce cours, et arrivé à ce stade le lecteur pourrait légitimement conclure que c'est une tâche très difficile. Qu'il se rassure, ce n'est pas difficile mais carrément impossible ! Plus précisément cela n'a pas de sens : chaque matériau peut – à un moment ou à un autre, et en fonction des conditions de sollicitation – présenter à peu près tous les comportement possibles. Trois exemples classiques.
Nous avons évoqué plus haut le matériau béton et sa non-résistance en traction. Différentes stratégies permettent de pallier cette faiblesse.
- Construire des structures ne travaillant qu'en compression. C'est l'art des bâtisseurs de cathédrale. C'est notamment ici que se situe le progrès majeur de l'art gothique par rapport à l'art roman (il s'agit ici de roches, mais celles-ci ont des propriétés voisines).
- Renforcer par des armatures métalliques les endroits susceptibles de travailler en traction. C'est le béton armé, et ces armatures supportent alors les contraintes de traction que le béton ne peut pas prendre en charge.
- Créer dans le béton une précontrainte de compression, qui viendra compenser les sollicitations extérieures de traction (béton précontraint). Cette précontrainte est en général créée par la mise en tension de câbles métalliques (câbles de précontraintes). Lors des premières tentatives, on n'avait pas imaginé que sur de longues échelles de temps (dizaines d'années) l'acier de ces câbles présenterait une relaxation des contraintes (<) , réduisant ainsi l'effet de la précontrainte. La technologie a ensuite évolué pour permettre le contrôle de la tension des câbles.
L'huile, lubrifiant de base, est en général considérée comme un fluide visqueux. Toutefois le tribologue constate que son élasticité joue, dans des conditions extrêmes rencontrées en lubrification, un rôle déterminant, qu'il importe de caractériser et de maîtriser.
Aux échelles géologiques, les roches qui constituent la lithosphère sont décrites par une loi de fluide visqueux non linéaire, loi de Norton-Hoff (>). Il en va de même de la calotte glacière antarctique. Le calcul de son écoulement permet de déterminer l'âge de la glace en fonction de sa position dans une carotte extraite en un point donné. C'est ainsi que la glaciologie permet d'obtenir des informations sur l'évolution du climat, voire de repérer des périodes d'intense activité volcanique.
Notre objectif n'est donc pas de trouver dans l'absolu la loi de comportement d'un matériau, mais plus modestement de choisir ou proposer à l'utilisateur un modèle adapté au problème particulier qu'il se pose (conditions de sollicitation), à la précision souhaitée et aux moyens disponibles (<). C'est entre autres ce qui justifie la grande importance de l'élasticité. Aucun matériau n'est vraiment élastique, mais le modèle élastique est suffisant et donc adapté pour de très nombreuses applications.