Les modèles de la Mécanique des Matériaux
En guise de conclusion à ce chapitre d'introduction, nous sommes maintenant à même de décrire dans ses grandes lignes la démarche qui sera suivie dans la suite et la structure générale des modèles dont la présentation fera l'objet de ce cours.
Description de l'état
La première étape de toute modélisation est de définir l'état du système, c'est-à-dire l'ensemble des informations nécessaires pour, à un instant donné, connaître complètement le matériau, notamment la contrainte. Techniquement on définit l'état comme ce qui permet de décrire complètement l'évolution ultérieure du matériau sous n'importe quelle sollicitation.
Pour un matériau élastique, l'état est complètement défini par sa déformation à l'instant considéré ε(t), et le modèle donne toutes les autres quantités (contraintes, énergie) en fonction de cette seule variable d'état. Remarquons que l'état peut alors aussi être défini par la contrainte σ(t). C'est un simple changement de variable.
Dans le cas général (<)
l'état sera défini par l'histoire passée du matériau ε(t−s) pour tout s ≥ 0, description sans doute complète mais pratiquement peu utilisable. Pour un matériau visqueux par contre, l'état sera défini par la déformation ε(t) et sa vitesse 
(t).
Rappelons que nous nous sommes limités à un cadre purement mécanique. Pour aborder les couplages thermo-mécaniques il faudra bien sûr rajouter la température.
Variables internes d'état
Dans une modélisation variables internes, on définit l'état du système à l'instant t en rajoutant à la déformation et sa vitesse, la valeur à l'instant t d'autres variables collectivement notées α (t). On écrit donc par exemple pour la contrainte
σ = σ (ε , α ; )
et on complète le modèle par une loi d'évolution qui permet de suivre, en fonction de la sollicitation appliquée, l'évolution de ces nouvelles variables
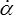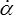= (ε , α ; )
La vitesse de déformation joue dans ce cadre un rôle spécifique, elle sera d'ailleurs souvent absente, et n'est pas à proprement parler une variable d'état. Nous y reviendrons très bientôt.
Les variables d'état ( ε , α ) se décomposent donc en deux groupes :
- la déformation ε(t) est dite « observable » ou mieux « contrôlable » car on peut dans un essai mécanique imposer ou contrôler son évolution,
- la variable interne α(t), au contraire, ne peut être imposée ; son évolution est subie et on ne pourra en général pas la mesurer directement. On a longtemps parlé de variable cachée.
On vérifie directement que les modèles rhéologiques rentrent dans ce cadre avec comme variables internes les déformations partielles des sous-éléments constituant le modèle.
D'un point de vue plus physique, ces variables intègrent, d'une manière plus ou moins explicite, les mécanismes microscopiques responsables du comportement observé. C'est, au-delà de sa grande commodité, l'avantage majeur de cette approche qui permet ainsi d'intégrer à la modélisation ce que l'on a pu comprendre ou observer des phénomènes microstructuraux sous-jacents.
Cette intégration pourra, selon le cas, être plus ou moins explicite ou qualitative. La structure des modèles rhéologiques par exemple peut refléter la structure interne du matériau mais ce n'est pas indispensable. Plus généralement, on peut utiliser pour décrire un système
- une approche phénoménologique, qui le considère comme une boite noire dont on observe la réponse,
- une approche microstructurale, qui consiste à prendre un tournevis pour démonter la boite noire et modéliser ses mécanismes élémentaires.
La réalité se situera en général entre ces deux extrêmes, et les variables internes que nous introduirons dans la suite traduiront symboliquement les mécanismes microscopiques sous-jacents qu'il sera souvent essentiel d'avoir à peu près identifiés.
Variables internes vs approche fonctionnelle
Pour une histoire de déformation ε(t) donnée, la loi d'évolution fournit une équation différentielle qui permet, par intégration, de calculer l'évolution des variables internes et donc la contrainte. Cette formulation variables internes conduit donc bien à la réponse fonctionnelle générale (<).
D'intenses discussions, à vrai dire un peu stériles, ont eu lieu autour des mérites respectifs de ces deux approches. Les tenants de l'approche fonctionnelle tiraient argument de sa généralité pour reléguer, parfois avec quelque mépris, l'approche variables internes à un simple cas particulier.Les tenants des variables internes rétorquaient alors que l'approche fonctionnelle reflétait en fait notre incapacité, voire notre incompétence, à caractériser correctement l'état microstructurel réel du matériau.
L'histoire a choisi son camp, et les modélisations variables internes se sont largement imposées ; les autres approches qui ont pu être envisagées en mécanique des matériaux n'ont pas réellement débouché. Attention toutefois à ne pas les mépriser complètement, elles sont dignes d'intérêt, notamment pour décrire certains aspects du comportement mal pris en compte par les modèles variables internes. Nous les laisserons de côté mais elles mériteraient parfois mieux, même si l'arrogance de certains de leurs partisans peut parfois agacer.
Le contexte thermodynamique
Le terme d'« état » suggère un contexte thermodynamique : les variables d'état, observables comme internes, définissent en effet l'état thermodynamique du système, et toute fonction d'état, l'énergie w par exemple, pourra s'exprimer en fonction d'elles. Nous écrivons donc
w = w(ε , α)
où la variable observable ε représente la déformation (scalaire ou tenseur), tandis que α représente le ou les variables internes (ensemble de valeurs scalaires ou tensorielles). On peut alors calculer la dissipation
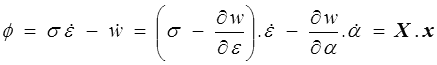
Aux flux thermodynamiques x = (,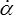) sont associées les forces thermodynamiques X = (σ v ,−H). Le premier terme correspond à la dissipation dite visqueuse et introduit la contrainte dite visqueuse. Le second terme correspond aux mécanismes internes représentés par α. La quantité H = ∂w / ∂α est la force thermodynamique associée à α (stricto sensu c'est plutôt −H, mais cet abus de langage est usuel).
Viscosité vs Elasticité instantanée
La contrainte sera donc en général donnée par
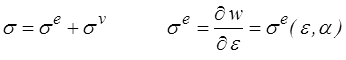
où σ e est la contrainte dite élastique ou réversible car la contrainte visqueuse σ v s'annule à l'équilibre (c'est du moins le cas dans tous les modèles classiques. Peut-on imaginer un modèle avec une contrainte visqueuse non nulle à l'équilibre, je ne le pense pas ; je n'en ai en tout cas jamais rencontré, mais l'imagination des modélisateurs est grande). C'est en fait par cette contrainte visqueuse que la vitesse de déformation intervient dans le modèle, et on parle alors de viscosité.
Très souvent il n'y aura pas de viscosité, la contrainte visqueuse sera nulle et la vitesse de déformation n'interviendra plus dans le modèle, qui, en conséquence, pourra supporter des discontinuités de déformation. On parle alors d'élasticité instantanée.
Viscosité ou Elasticité instantanée ? C'est une première option importante dans le choix d'une modélisation. La question à se poser est de décider comment le modèle doit réagir à une contrainte appliquée instantanément :
- par un saut de déformation ? Le modèle est alors avec élasticité instantanée (sans viscosité),
- par un saut de la vitesse de déformation ? Le modèle est alors visqueux.
Nous parlons bien ici de modèle et non de matériau: quant à savoir comment le matériau lui-même réagit à une contrainte instantanément appliquée, c'est une interrogation aussi oiseuse que de chercher « la » loi de comportement de ce matériau (<) .
On remarquera aussi que nous avons ici brisé la symétrie jusqu'à présent complète entre contrainte et déformation.
Dans un modèle avec élasticité instantanée un saut de contrainte est associé à un saut de déformation
σ(t) discontinu 
ε(t) discontinu
Dans un modèle visqueux un saut de contrainte est associé à un saut de vitesse de déformation
σ(t) discontinu (t) discontinu
Il n'existe pas de modèle (raisonnable, on peut toujours tout imaginer) pour lequel un saut de déformation soit associé à un saut de vitesse de contrainte
ε(t) discontinu 
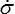(t) discontinu (σ continu)
C'est ce que Mandel appelle le principe de non-dualité.
Modèle standard généralisé
Nous avons identifié les forces et les flux thermodynamiques. Tout est donc en place pour appliquer la TPI et mettre en ouvre l'hypothèse de dissipativité normale. Ceci conduit au modèle standard généralisé (pourquoi standard et pourquoi généralisé ? l'origine de cette terminologie est historique, j'y reviendrai plus loin). On introduit un potentiel de dissipation Ω(x) = Ω( , 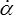) et l'on écrit
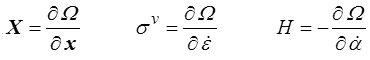
L'écriture inverse, pourtant bien utile, posera problème dans le cas indépendant des vitesses. Nous nous bornerons ici à l'expliciter dans le cas des modèles avec élasticité instantanée. Le formalisme direct donne alors
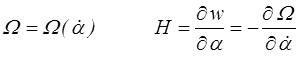
tandis que le formalisme inverse s'écrira sans difficulté pour un modèle dépendant des vitesses
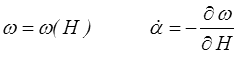
Mais pour un modèle indépendant des vitesses il nous faudra alors, comme nous l'avons vu plus haut (<), introduire un convexe, sa fonction indicatrice et le sous-différentiel associé.
D'un point de vue pratique et en nous limitant au cas régulier qui le plus souvent suffira , on écrira la loi d'évolution à partir d'une fonction seuil f(X) = f(H)
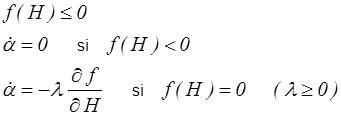
où le multiplicateur plastique λ ≥ 0 est indéterminé (<). Cette formulation peut sembler bien ésotérique. Nous verrons plus loin qu'elle est parfaitement utilisable et insistons à nouveau sur le fait que c'est une conséquence incontournable du comportement indépendant des vitesses.
Conclusion provisoire
Tout cela peut paraître bien abstrait et effectivement ça l'est. Ne vous inquiétez pas. C'est un cadre général dans lequel vont progressivement se mettre en place les modèles que l'on peut développer et il aurait été dommage de ne pas l'introduire dès à présent. Mais c'est aussi, pour l'instant, une coquille vide qui ne prendra son sens qu'au fur et à mesure que nous la remplirons. J'invite le lecteur à y revenir régulièrement.
Face à un problème de modélisation notre démarche impliquera trois volets.
- Choisir les variables internes, représentations macroscopiques phénoménologiques des mécanismes microscopiques.
- Ecrire la loi de comportement , c'est-à-dire la manière dont ces variables modifient le comportement, en particulier les contraintes.
- Ecrire les lois d'évolution, c'est-à-dire la manière dont ces variables changent en fonction de la sollicitation appliquée.
Le cadre standard généralisé fournira dans ce contexte un guide très commode pour le troisième volet, au moins en première approche : contrairement aux relations d'Onsager − jamais contredites à ce jour − l'hypothèse de dissipation normale n'est pas indiscutable, et nous rencontrerons des cas où il est nécessaire ou commode de s'en affranchir.