Modèles viscoélastiques
Les modèles rhéologiques viscoélastiques (<) - c'est-à-dire formés de ressorts et d'amortisseurs - s'inscrivent tout naturellement dans ce cadre.
Kelvin et Maxwell
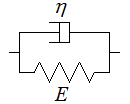Le modèle de Kelvin (<)
, montage parallèle d'un ressort et d'un amortisseur, est le plus simple. Sa loi de comportement
σ = E ε + η 
devient en transformée de Laplace-Carson
σ* = E ε* + η p ε* = (E + η p) ε*
Les modules opérationnels sont donc
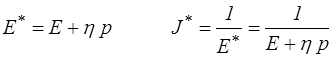
soit, en revenant à l'original,
E* = E + η p E (t) = E + η δ(t)
La fonction de relaxation fait intervenir une fonction de Dirac, ce qui correspond à l'impossibilité d'imposer une déformation instantanée − matériau visqueux au sens où nous l'avons défini plus haut (<) . Rappelons que toutes les fonctions que nous manipulons sont en fait − bien que ceci soit tout à fait transparent pour l'utilisateur − des distributions.
La fonction de fluage J (t) s'obtient directement à partir du mini-formulaire (<)
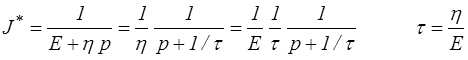
d'où, par utilisation de la formule appropriée
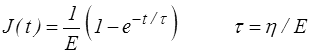
et on retrouve bien évidemment le résultat obtenu directement par intégration de l'équation différentielle (<) .
Modèle de Kelvin.
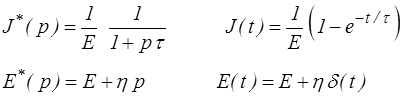
On ne s'inquiétera pas du risque de confusion entre E, raideur du ressort, et E (t), fonction de relaxation, elle disparaîtra bientôt.
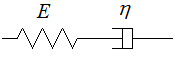Pour le modèle de Maxwell, c'est à peine plus difficile. Partant de la loi de comportement (<)
σ = E εe = η a ε = εe + εa
on obtient en transformée de Laplace-Carson
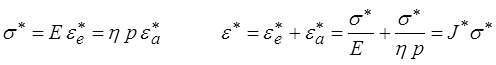
D'où la fonction de fluage
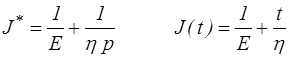
puis la fonction de relaxation
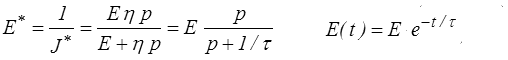
toujours par utilisation du mini-formulaire, et on retrouve bien évidemment les résultats obtenus par intégration directe (<) . On remarquera que, comme nous l'avions annoncé, ce calcul prend automatiquement en compte la discontinuité à l'origine, alors que nous avions dû la traiter séparément avant de pouvoir intégrer l'équation différentielle.
Modèle de Maxwell.
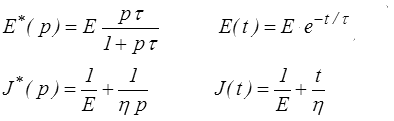
Poynting et Zener
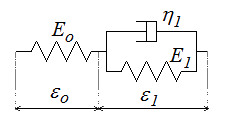Le modèle de Poynting ou Poynting-Thomson est le montage en série d'un ressort et d'un modèle de Kelvin. On écrira donc, avec des notations naturelles,
ε = εo + ε1 σ = σo = σ1 = Eo εo = E1 ε1 + η11
soit en transformée de Laplace-Carson (dont on peut remarquer ici l'efficacité)
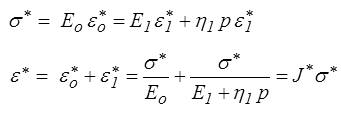
d'où la fonction de fluage
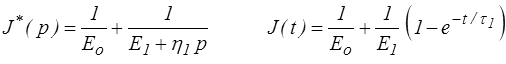
en utilisant pour le second terme le résultat obtenu pour le modèle de Kelvin.
Pour la fonction de relaxation, il faut prendre l'inverse de cette fraction rationnelle
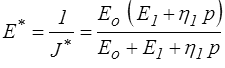
d'où l'on pourrait tirer E (t) par utilisation du mini-formulaire après décomposition de cette fraction en éléments simples. Je laisse ce calcul de côté, car nous verrons très bientôt une méthode plus économique et porteuse de sens pour obtenir cette fonction de relaxation E (t).
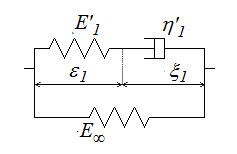Je passe maintenant au modèle de Zener (avec des notations un peu moins naturelles mais qui trouveront rapidement leur raison d'être)
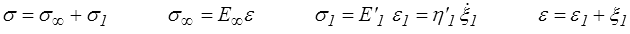
soit en transformée de Laplace-Carson
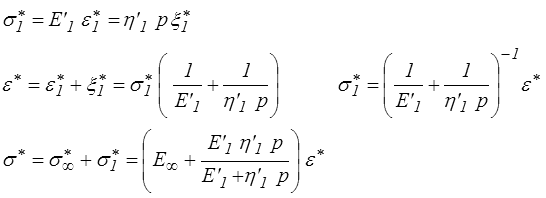
et en utilisant le résultat obtenu pour le modèle de Maxwell
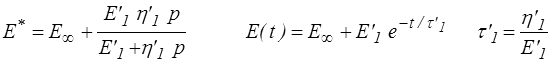
Pour obtenir la fonction de fluage on écrira
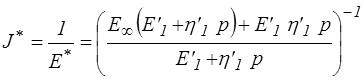
Le retour à l'original permettrait ensuite de calculer J (t).
On peut maintenant remarquer que ces deux modèles, Poynting et Zener, conduisent pour J * et E * à deux fonctions rationnelles de la forme
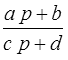
et, sous réserve de l'identification de ces fractions, on pourra affirmer que ces deux modèles coïncident. Prenons par exemple, pour réaliser cette identification, la fonction de relaxation. Nous devons donc écrire
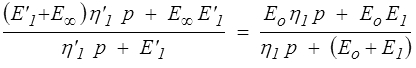
L'identification de ces deux fractions rationnelles va nous donner 3 relations (les 4 coefficients ne sont définis qu'à une constante multiplicative près) qui vont nous permettre de calculer E'1, E∞ et η'1 en fonction de Eo, E1 et η1 ou réciproquement, ce qui permettra d'identifier ces deux modèles. Ce calcul algébrique peut être mené directement, mais il est plus astucieux d'examiner les limites p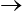 
0 et p 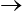∞. On obtient alors respectivement
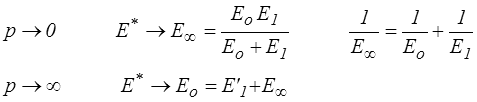
Ces deux relations donnent ( E∞ , E'1 ) en fonction de ( Eo , E1 ) et réciproquement. La relation entre η1 et η'1 s'obtient ensuite simplement, par exemple
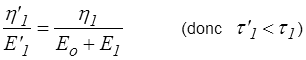
Poynting et Zener sont donc en fait deux représentations équivalentes du même modèle, et on utilisera l'un ou l'autre selon ce qui sera le plus commode. C'est pour cette raison que nous n'avons pas directement calculé la fonction de relaxation pour Poynting : il est plus simple d'utiliser le résultat obtenu pour Zener.
Le comportement en fluage et relaxation de ce modèle est représenté ci-dessous.
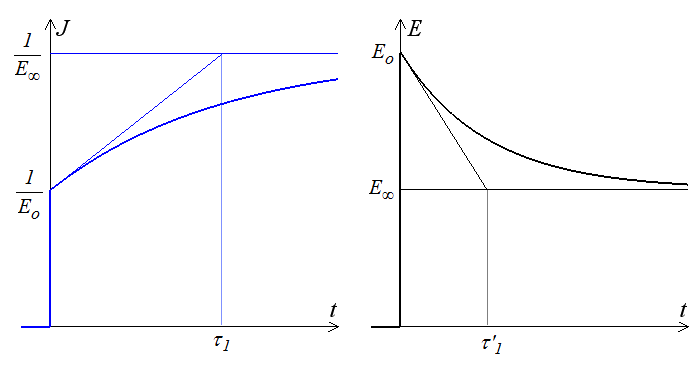
On constate que Eo correspond à la limite t 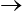0 ( p 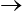∞ ) et E∞ à la limite t 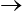∞ ( p 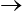0 ), ce qui motive la notation utilisée. Nous y reviendrons.
Remarquons aussi que la loi de comportement transformée
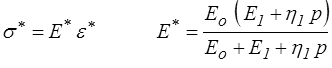
peut aussi s'écrire
( Eo + E1 + η1 p ) σ* = Eo ( E1 + η1 p ) ε*
ce qui, en revenant aux fonctions originales, correspond à une équation différentielle
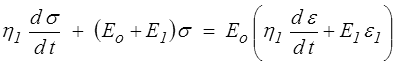
forme différentielle de la loi de comportement.
Autres modéles simples
Les autres modèles viscoélastiques simples s'étudieraient de la même manière. On montrerait par exemple que les deux versions proposées pour le modèle de Jeffreys (<) correspondent bien au même modéle à condition d'identifier correctement les 3 constantes. Le lecteur pourra, en guise d'exercice, déterminer par exemple la fonction de fluage J (t), correspondant au modèle de Burgers. Je n'insiste pas car nous allons immédiatement retrouver cela dans un contexte plus général