Introduction à la Mécanique Analytique
Insistons à nouveau sur le fait que nous sommes ici en dehors du cadre de ce cours. Ces considérations sont toutefois tellement importantes d'un point de vue théorique – en mécanique statistique comme en physique quantique – qu'il serait dommage de ne pas les évoquer dans le panorama général que je cherche à dresser.
Lagrangien et Hamiltonien d'un système
La fonction
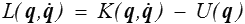
qui intervient dans l'intégrale d'action est appelée lagrangien du système (conservatif) et les équations de Lagrange (<) s'écrivent aussi
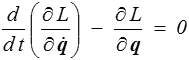
Elles conduisent à un système d'équations différentielles du second ordre qui avec des conditions initiales
permettront de déterminer l'évolution des N fonctions q(t), définissant ainsi complètement le mouvement du système.
On définit alors les impulsions généralisées p(t)
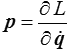
et la fonction de Hamilton (ou hamiltonien) du système H ( p , q ) par
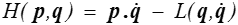
D'un point de vue mathématique il s'agit d'une transformation de Legendre que nous rencontrerons plus tard dans d'autres contextes. En fait d'ailleurs, vous en avez sans doute déjà rencontré Quand ?
En thermodynamique classique des fluides on écrit le premier principe
dU = − p dV + T dS
d'où l'on tire, à partir de la fonction U ( V , S ) les lois d'état
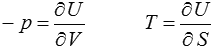
On dit que U ( V , S ) est un potentiel thermodynamique et on en introduit traditionnellement trois autres : l'enthalpie H , l'énergie libre F et l'enthalpie libre G. L'enthalpie, par exemple,
est, au signe près, la transformée de Legendre de l'énergie interne U par rapport au couple de variables conjuguées ( V , − p ). Elle permet en quelque sorte d'échanger le rôle des variables V et − p. De même le hamiltonien permet d'échanger les rôles de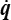 
et de p.
Hamiltonien et Energie
L'énergie cinétique K est fonction quadratique des vitesses. On peut donc écrire
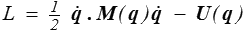
avec une matrice de masse M qui en général dépendra de q. L'impulsion généralisée p est alors
De sorte que la produit scalaire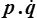 
est égal à deux fois l'énergie cinétique. Il vient alors
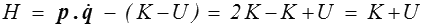
Le hamiltonien n'est donc rien d'autre que l'énergie totale du système, exprimée en fonction des variables p et q.
Un cas particulier important est celui des systèmes linéaires pour lequel la matrice de masse est constante et le potentiel U quadratique
où M est la matrice de masse et A la matrice de raideur (assez traditionnellement notée K, mais la lettre est ici déjà utilisée !).
Le lagrangien et les équations de Lagrange sont alors
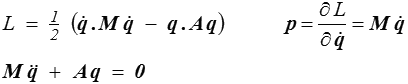
tandis que le hamiltonien est donné par
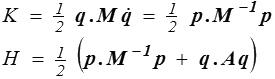
Les équations canoniques
Partant de la définition de H, on obtient par différentiation
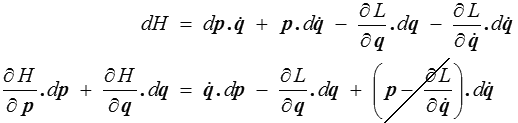
Le dernier terme s'annulant par la définition de l'impulsion généralisée p. On en tire par identification
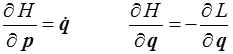
Mais les équations de Lagrange donnent
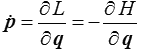
système d'équations différentielles du premier ordre qui par intégration donnera l'évolution des variables p ( t ) et q ( t ) à partir de la fonction H ( p , q ) et des conditions initiales
D'un point de vue pratique, cette formulation est complètement équivalente à la formulation lagrangienne, mais on l'utilise en fait beaucoup moins (pourquoi ? je ne sais pas vraiment ! sans doute parce qu'elle peut sembler plus abstraite.)
La dérivée par rapport au temps de H est
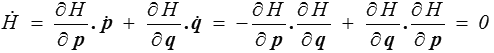
ce qui, bien évidemment, correspond à la conservation de l'énergie totale.
On a vu plus haut que
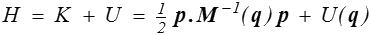
Les équations de Hamilton sont donc
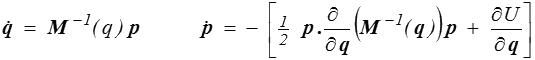
équations un peu complexes, au moins pour la seconde. Dans le cas linéaire par contre, tout se simplifie en
Le théorème de Liouville
Cette introduction à la mécanique analytique sort, répétons-le, du cadre de ce cours. Pour la conclure et vous suggérer sa puissance, je ne résiste pas à la tentation de vous présenter le célèbre théorème de Liouville. L'espace de base de la mécanique est maintenant l'espace des phases, c'est à dire l'espace à 2 N dimensions des ( qi , pi ) . Le mouvement d'un système mécanique, calculable par intégration du système différentiel formé par les équations de Hamilton, est alors décrit par la trajectoire ( qi (t) , pi (t) ) du point représentant le système dans cet espace.
Si maintenant l'on suit dans leur mouvement un ensemble de « points » occupant à l'instant t un domaine 
de volume Vo. On montre alors que ce volume ne change pas au cours du temps.
Théorème de Liouville.
Le volume d'un domaine est, dans l'espace des phases, un invariant du mouvement : il reste constant.
La démonstration de ce théorème est tout à fait abordable mais nous ne disposons pas encore des outils appropriés (nous les verrons plus tard dans le contexte différent de la MMC, je pourrais alors vous donner une esquisse de sa démonstration) Il peut aussi sembler abstrait, et pourtant une de ses conséquences est lourde de sens.
Il est banal d'affirmer que l'on ne peut déterminer la position et l'impulsion (c'est-à-dire la vitesse) d'un système que de manière approchée. Supposons, en prenant pour fixer les idées un seul degré de liberté, que l'on puisse localiser sa position et son impulsion dans un petit rectangle Δqo x Δpo. Le théorème de Liouville affirme alors que, au cours du mouvement, il restera confiné dans un rectangle Δq x Δp, avec
Δq x Δp = Δqo x Δpo
On pourra gagner de la précision sur la position, mais seulement au dépens de celle sur la vitesse et vice-versa. Mais n'est-ce pas plus ou moins ce qu'affirment les relations d'incertitudes de Heisenberg, un des piliers de la physique quantique ? Certes l'incertitude est ici de nature très différente, mais l'analogie est troublante.