Comportement et essais mécaniques
Les lois de comportement
Pour compléter la formulation d'un problème de MMC, il nous manque la loi de comportement qui nous fournira les 6 équations manquantes.
Nous ne discuterons pas ici la structure générale de cette loi de comportement ( ce sera en fait le théme du cours Comportement des Matériaux (>) ) et nous retiendrons simplement qu'elle exprime une relation entre les tenseurs des contraintes et des déformations, et plus spécifiquement qu'elle doit permettre de déterminer les contraintes à partir des déformations ou inversement, de déterminer les déformations à partir des contraintes. Le bilan énergétique
ø = σij 
ij − 
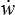≥ 0
(<) jouera souvent un rôle essentiel.
On notera que, contrairement à tout ce qui a été discuté jusqu'à présent et qui était tout à fait général, nous entrons maintenant dans un domaine très varié : la diversité des lois de comportement répond en fait à la diversité des comportements et des matériaux. C'est par la loi de comportement que l'on prend en compte la nature du matériau (verre, acier, béton, bois, etc..., la liste est longue, même en nous limitant aux solides avérés).
La mécanique des milieux continus (contraintes, déformations, équations du mouvement) est générale. La loi de comportement est, par essence, particulière.
Essais mécaniques
Puisqu'elle caractérise, dans une situation donnée, les propriétés physiques d'un matériau, cette loi est, également par essence, d'origine expérimentale. En principe tout semble simple : on veut caractériser expérimentalement la relation contraintes-déformations ; il suffit donc d'imposer la déformation et de mesurer la contrainte ou vice versa.
Oui, mais... on ne sait imposer que les déplacements ou les efforts à la frontière (<) et − pire − si diverses techniques permettent de mesurer les déformations, on ne sait pas mesurer les contraintes.
Il faudra donc, pour caractériser expérimentalement la loi de comportement, imaginer des « structures » suffisamment bien choisies pour pouvoir remonter aux déformations et aux contraintes. C'est ce que l'on appelle les essais mécaniques.
Sollicitations élémentaires
D'un point de vue théorique, deux essais joueraient, si on savait les réaliser facilement (malheureusement tel n'est pas le cas), un rôle important en Mécanique des Matériaux. Considérons pour commencer l'essai de compression hydrostatique ou contraction isotrope
Un objet, sphérique par exemple, mais on peut montrer que les résultats qui suivent sont indépendants de la forme de l'objet, est plongé dans une enceinte sous pression. Les conditions aux limites sont alors
σij nj = −Po ni
On obtient alors pour un matériau homogène un état de contraintes de pression hydrostatique uniforme
σij = −Po δij
et une déformation homogène, qui pour un matériau isotrope − et, sauf mention explicite du contraire, nous nous limiterons désormais à ce cas pour ce cours − correspondra à une dilatation uniforme
ui = − α xi ( εij = − α δij )
Il suffit donc d'imposer Po et de mesurer α, c'est-à-dire en fait la variation de volume. Cette mesure est toutefois beaucoup plus délicate qu'il n'y paraît, et sauf cas particulier cet essai n'est utilisé que très marginalement en mécanique des solides. De plus, on verra plus tard que cet essai ne fournit pas les caractéristiques les plus importantes d'un matériau.
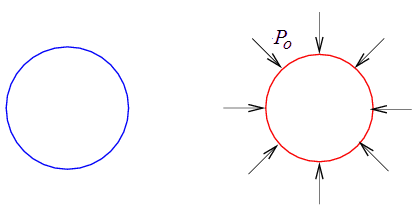
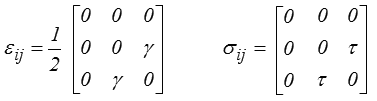
Le cisaillement simple est défini par
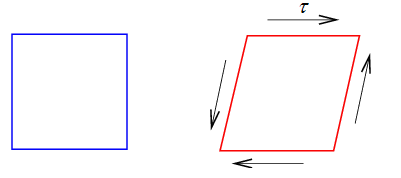
Cet essai correspond (toujours pour un matériau isotrope) à la solution suivante
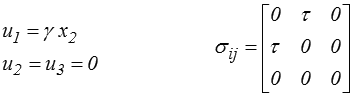
Si l'on savait le réaliser, cet essai nous donnerait des résultats très importants ! Malheureusement on ne sait pas, tout au moins sous cette forme : on verra plus loin que l'on peut toutefois s'en approcher. C'est la raison pour laquelle on s'y réfère souvent en Mécanique des Matériaux, même si l'on ne sait pas le réaliser directement.
Traction simple
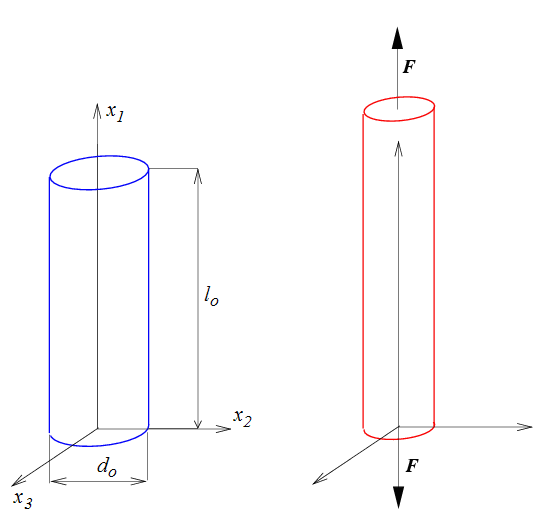
On prend une éprouvette cylindrique (en général circulaire ou, pour des matériaux conditionnés en plaques, parallélipipédique) et on lui impose un effort longitudinal F. On constate alors (ou on démontre : en réalité les choses sont un petit peu plus compliquées, mais nous en resterons là, au moins pour l'instant) que la solution est
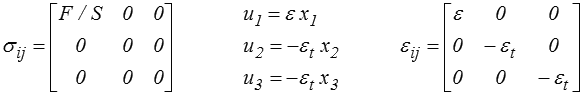
ce qui correspond à un allongement longitudinal ε = Δl/lo et une contraction transversale εt = Δd/do (là encore en nous limitant aux matériaux isotropes).
C'est en fait l'essai de référence en mécanique des solides : il est (relativement) facile à réaliser, il est théoriquement bien fondé par le principe de Saint Venant (cf. Polycopié VII-1.1), et il permet une bonne caractérisation du comportement. Il a toutefois ses limitations, notamment par l'apparition de la striction − diminution locale et brutale de la section.
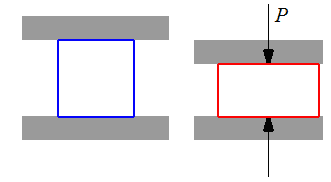L'essai de compression simple par écrasement d'un bloc entre les deux plateaux d'une presse avec contact sans frottement est très voisin.
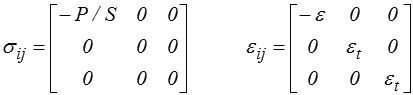
Le problème majeur est ici la réalisation, par une lubrification judicieuse, des conditions de contact sans frottement.
Essais homogènes
Tous ces essais sont des essais homogènes, c'est-à-dire des essais pour lesquels les champs de contraintes et de déformations sont uniformes (indépendants de la position)
σij = σijo ui = βijo xjo εij = ½ ( βijo + βjio )
On peut alors obtenir directement les contraintes (non mesurables) à partir de la mesure des efforts.
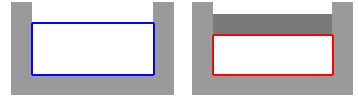On peut par exemple citer l'essai oedométrique fréquemment utilisé pour les matériaux pulvérulents ou sans grande cohésion : on écrase alors le matériau dans un moule rigide avec
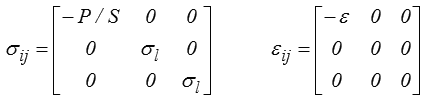
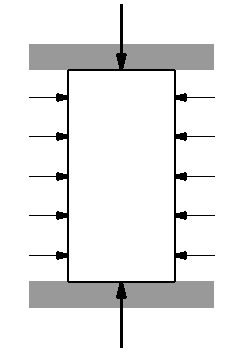
Pour ces matériaux on réalise également un essai dit « triaxial » qui est en fait un essai de compression en présence d'une pression latérale assurant la cohésion. On devrait plutôt parler d'un essai triaxial de révolution.
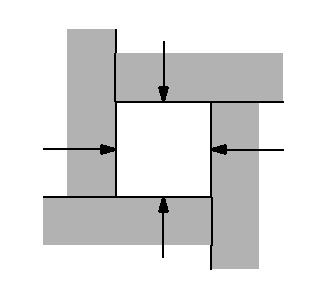
Il existe au monde quelques presses triaxiales permettant de réaliser de vrais essais triaxiaux avec 3 contraintes indépendantes
Signalons pour terminer l'essai de compression plane (Channel die test en anglais)
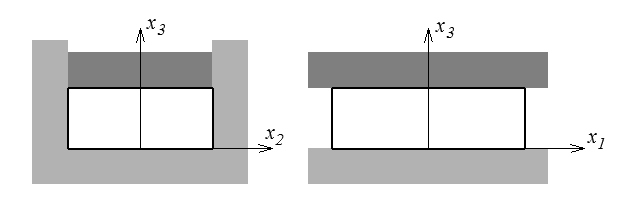
où une éprouvette est écrasée dans un canal qui interdit tout mouvement latéral dans une direction
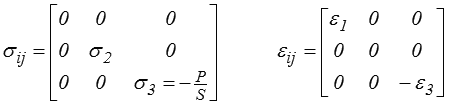
Cet essai est notamment utilisé pour les monocristaux (donc pour des matériaux anisotropes, l'analyse est donc plus délicate).
Torsion d'un tube mince
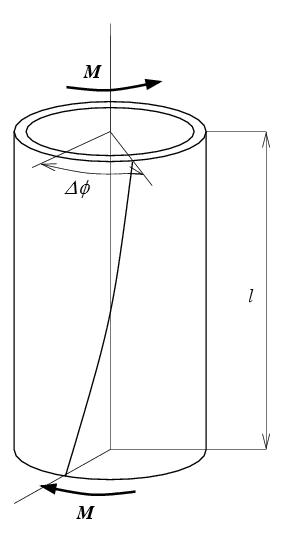L'essai de torsion, simple dans sa réalisation, sera analysé plus loin (>) et n'est pas un essai homogène. Par contre si l'on réalise cet essai sur un tube mince alors on peut, en première approximation, négliger la variation de contrainte et de déformation dans l'épaisseur.
Cet essai permet donc de réaliser de fait une sollicitation de cisaillement simple : en notant Δø la rotation relative des deux sections d'extrémité et M le couple de torsion exercé, on obtient
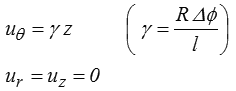
soit, pour les déformations et les contraintes,
et le couple de torsion engendré est
M = π R 2e τ
La mesure de M et Δ ø permet de déterminer τ en fonction de γ et donc de réaliser l'essai de cisaillement évoqué plus haut.
D'un point de vue pratique, cet essai est malheureusement limité par un phénomène de voilement du tube qui, de fait, le limite à de très petites déformations.
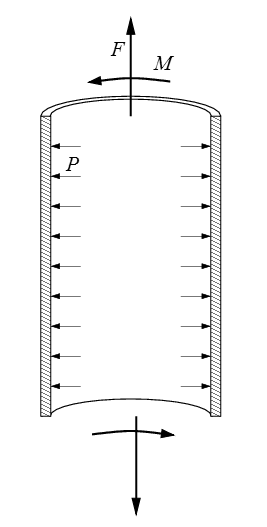
Plus généralement, les machines d'essais réalisant cet essai de torsion permettent souvent de superposer un effort de traction-compression engendrant une contrainte longitudinale
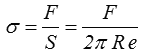
Ces essais de traction-torsion sont fort intéressants car ils permettent d'imposer, indépendamment l'une de l'autre, deux composantes du tenseur des contraintes.
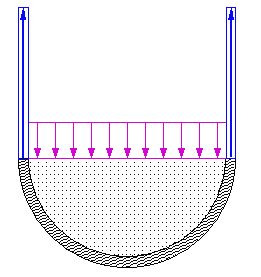On peut même rajouter à l'intérieur du tube une pression interne qui va engendrer une contrainte que l'on calcule aisément en écrivant l'équilibre d'un demi-cylindre
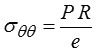
Quant à la contrainte σrr elle varie entre 0 à l'extérieur (surface libre) et − P à l'intérieur, elle sera donc pour un tube mince négligeable par rapport à σθθ. On peut donc ainsi réaliser un état de contraintes excitant trois composantes
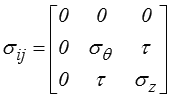
Essais quasi homogènes
On utilise souvent pour caractériser le comportement des tôles l'essai dit de traction plane.
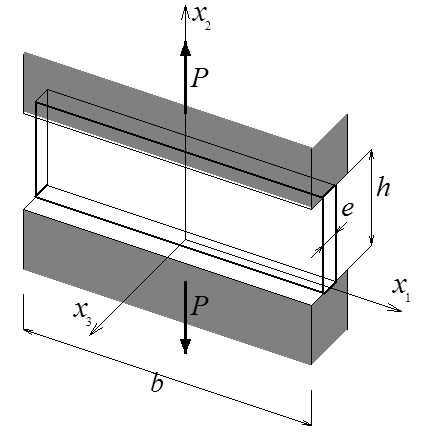
Cet essai consiste à réaliser un essai de traction sur une plaque très large. On interdit ainsi les mouvements transversaux de sorte que, en première approximation,
Cette solution n'est évidemment pas entièrement satisfaisante puisque l'existence d'une contrainte σ1 est en contradiction avec la condition de surface libre qui, sur les faces latérales x1 = ± b /2, impose σ1 = 0. Néanmoins ces effets de bord peuvent, pour une éprouvette large (b >> h), être, en première approximation, négligés. On peut d'ailleurs contrôler cette approximation par un calcul éléments finis et améliorer un peu l'homogénéité du champ de contraintes en modifiant légèrement la forme de l'éprouvette.
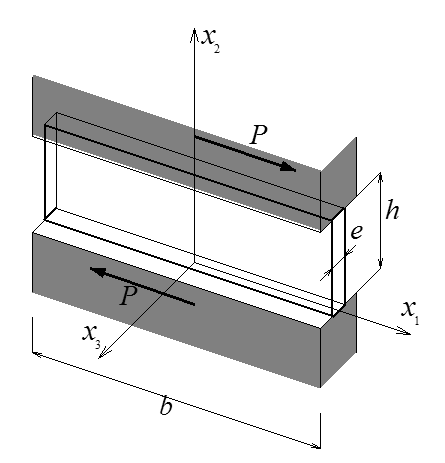
Un essai de cisaillement simple peut être réalisé dans les mêmes conditions.
Là encore l'existence de cisaillement τ = σ21 est en contradiction avec la condition de surface libre, induisant des effets de bord que l'on espère pouvoir plus ou moins négliger.
Essais non homogènes
Les essais complètement non homogènes ne permettent pas d'évaluer directement les contraintes. Leur analyse passe donc nécessairement par le couplage avec un calcul de structures. Le développement des méthodes numériques et les progrès de l'informatique facilitent toutefois ce couplage. Ces essais sont principalement utilisés pour caractériser le comportement sous des états de contraintes complexes irréalisables autrement.
Citons, par exemple,
-
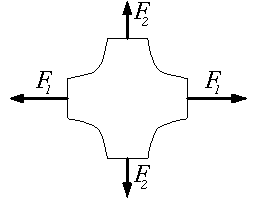l'essai de traction biaxiale sur éprouvette en croix qui engendre des états de tension biaxiale ; -
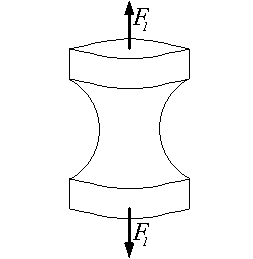l'essai de traction sur éprouvette entaillée qui permet d'engendrer au coeur de l'éprouvette un état de tension triaxiale.
Mentionnons également les essais d'indentation, relativement faciles à utiliser et non destructifs. Ils sont encore peu utilisés pour la construction de lois de comportement, mais il s'agit là d'un domaine en évolution.
Signalons enfin les développements récents des méthodes dites « de champ » qui visent à déterminer, par différentes métrologies, la totalité du champ de déplacement. Ces méthodes ouvrent des perspectives intéressantes et devraient se diffuser largement dans les années qui viennent.