Le théorème des puissances virtuelles
Puissances virtuelles
La loi des puissances virtuelles (principe ou théorème ? Nous en avons déjà discuté ; dans le cadre de ce cours c'est un théorème) (<)
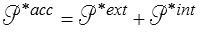
est, au même titre que la loi fondamentale, à « la base de la mécanique ». Elle est toutefois plus abstraite et sa transcription en mécanique des milieux continus n'est assurément pas directe. La description du mouvement d'un milieu continu permet naturellement de définir un champ de vitesses virtuelles V *(x) ainsi que la puissance virtuelle des quantités d'accélération
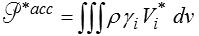
Le postulat de Cauchy permet, quant à lui, de définir, tout aussi naturellement, la puissance virtuelle des efforts extérieurs
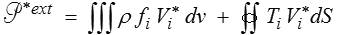
C'est la puissance virtuelle des efforts intérieurs qui pose problème, et la définition que nous en avons donnée dans le cas d'un système de particules en interaction (<) ne nous aide guère.
On démontre donc le :
Théorème des puissances virtuelles
C'est la loi des puissances virtuelles, posée comme étant vraie, qui va en fait nous permettre d'obtenir la bonne forme de cette puissance des efforts intérieurs. Restera ensuite à se convaincre que cette procédure − à tout le moins abstraite et détournée − est bien raisonnable et porteuse de sens physique.
Théorème des puissances virtuelles
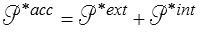
avec
Le tenseur D*ij, dual du tenseur des contraintes, est appelé tenseur des taux de déformations (ici virtuelles) et nous justifierons plus loin cette terminologie.
Démonstration du théorème
Pour démontrer le théorème nous partons de l'équation du mouvement, valable partout. Nous en faisons en chaque point le produit scalaire par la vitesse virtuelle V *(x) et nous intégrons sur un domaine matériel D (a priori quelconque, mais on prendra en général le domaine d'étude tout entier)
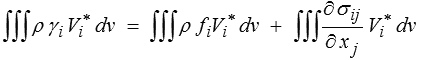
Le théorème de la divergence (<) permet ensuite de transformer la dernière intégrale
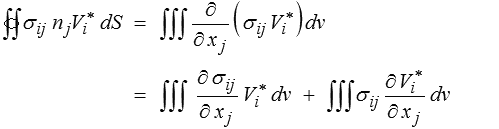
On obtient donc finalement
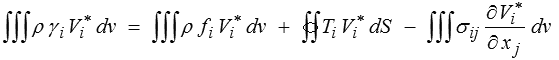
où l'on reconnaît au premier membre la puissance des quantités d'accélération et au second membre celle des efforts extérieurs complétée par un terme supplémentaire que l'on va donc pouvoir interpréter comme la puissance des efforts intérieurs
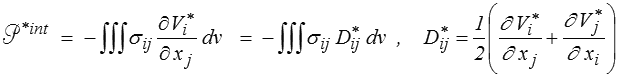
puisque, le tenseur des contraintes étant symétrique, on peut remplacer le tenseur gradient des vitesses ∂V *i / ∂xj par sa partie symétrique D*ij.
Mouvement de solide rigide
Une première étape dans l'interprétation de ce résultat est fournie par le théorème suivant.
Théorème.
Une CNS pour que le tenseur des taux de déformation soit identiquement nul est que le champ des vitesses soit rigidifiant
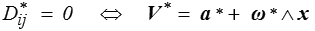
La condition suffisante est directe : si le champ des vitesses est rigidifiant
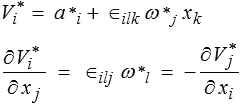
d'après les propriétés d'antisymétrie des symboles de permutation de Livi Civita (cf. Polycopié A-2.2) ∈ijk , que l'on prendra soin de ne pas confondre avec le tenseur εij qui apparaîtra très bientôt.
La réciproque est plus laborieuse et nous l'admettrons (nous y reviendrons en fait plus loin, lorsque nous évoquerons les équations de compatibilité).
La puissance virtuelle des efforts intérieurs est donc, comme il convient, bien nulle dans tout mouvement rigidifiant (<).
Théorème des travaux virtuels
En mécanique des solides on utilise plus volontiers le théorème des travaux virtuels. En fait il s'agit d'un simple changement de notation : si l'on remplace le terme vitesse virtuelle et sa notation V par déplacement virtuel noté u* (ou plus souvent δu) le théorème devient
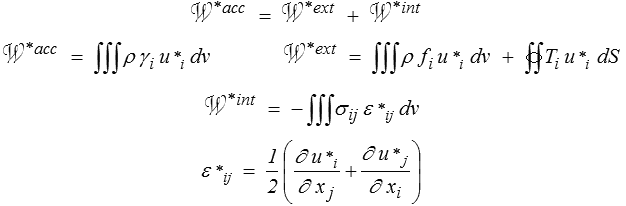
Théorème des travaux virtuels.
Le travail virtuel des quantités d'accélération est égal au travail virtuel des efforts extérieurs et intérieurs.
Ce n'est donc, par rapport aux puissances virtuelles, qu'un changement de notation et d'interprétation. Ceci introduit toutefois le tenseur des déformations infinitésimales εij qui joue, en MMC petites perturbations, un rôle essentiel.
Formulation faible
D'un point de vue mathématique, le théorème des puissances virtuelles ou des travaux virtuels est la formulation faible des équations du mouvement. On l'obtient bien en effet en faisant, dans l'espace des champs vectoriels, le produit scalaire de l'équation du mouvement par un champ « virtuel » arbitraire.
Remarquons toutefois que, contrairement aux systèmes discrets étudiés jusqu'à présent, nous sommes maintenant dans un espace fonctionnel de dimension infinie et que cette « formulation faible » n'est plus tout à fait équivalente à la formulation forte usuelle (différentielle). Contrairement à ce que l'on pense souvent, elle est plus « physique » car, n'imposant pas aux fonctions en cause d'être dérivables, elle autorise certaines discontinuités que la physique autorise également.
Energie et dissipation
Nous pouvons maintenant revenir sur le bilan énergétique qu'exprime le premier principe de la thermodynamique (<)
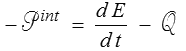
que nous pouvons maintenant écrire
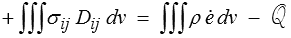
où e désigne l'énergie interne spécifique (c'est-à-dire par unité de masse). Pour aller plus loin il faudrait modéliser les échanges de chaleur, et nous ne le ferons pas dans ce cours. Les échanges de chaleur sont en effet généralement négligés en mécanique des solides. Ce bilan reste néanmoins essentiel même si l'on ne s'intéresse pas au problème thermique. Dans une approche purement mécanique, en effet, le dernier terme représente la chaleur restituée au système et donc « perdue » pour le mécanicien − le mot « perdue » n'est toutefois pas politiquement (pardon ! thermodynamiquement) correct, mais pour nous, mécaniciens, la réalité est bien là −. Dans ce contexte purement mécanique, le second principe de la thermodynamique se traduit simplement par le fait que cette énergie dissipée est positive (système dissipatif) ou nulle (système conservatif).
En HPP cette relation devient
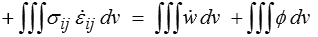
où w = ρo e représente l'énergie par unité de volume (en HPP ρ = ρo au premier ordre) et où ø représente la dissipation (c'est-à-dire le taux de dissipation d'énergie par unité de volume).
Pour l'élément de volume, ce bilan devient
σij 
ij =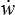 
+ ø ø ≥ 0
Ce bilan énergétique jouera un rôle fondamental dans l'écriture des lois de comportement.