Représentations géométriques des déformations
Représentations d'un tenseur
Nous avons présenté plus haut (<) diverses représentations géométriques du tenseur des contraintes. Toutes ces représentations peuvent en fait être mises en place pour n'importe quel tenseur du second ordre symétrique. On pourra ainsi construire pour le tenseur des déformations
- la quadrique des déformations,
- un ellipsoïde de Lamé,
- le cercle de Mohr des déformations.
Ces représentations − parfaitement licites d'un point de vue mathématique ou géométrique − perdent toutefois leur sens physique car le vecteur E = ε n n'a malheureusement aucune signification physique.
Transformation d'un vecteur matériel
On peut toutefois redonner au cercle de Mohr une signification géométrique intéressante.
Attention, contrairement à l'ensemble de ce cours d'introduction à la MMC, finalement très classique et traditionnel, cette présentation du cercle de Mohr des déformations de l'est pas. Le lecteur, même averti, pourra y trouver profit. Elle se prolongera d'ailleurs plus tard lorsque nous aborderons les grandes transformations.
Pour cela il est nécessaire de revenir à la transformation locale, c'est-à-dire de réintroduire la rotation.
Le mouvement local est en effet défini par le tenseur β gradient des déplacements
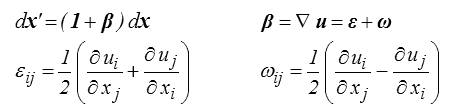
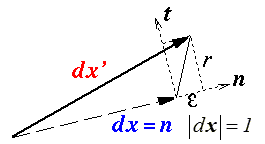Un vecteur matériel dx = dx n subit donc
- une variation de longueur caractérisée par l'allongement ε(n)
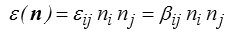
- une rotation r(n) définie par
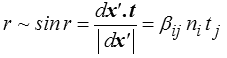
où, comme pour les contraintes, t désigne le vecteur orienté à +π / 2 de la direction n du vecteur dx.
En fait, ε et r sont les composantes du vecteur du correspondant à un vecteur dx unitaire dans la direction n = (cosθ, sinθ).
On obtient alors directement
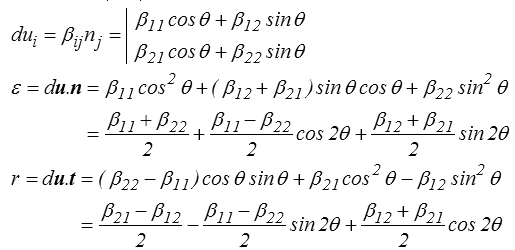
Cercle de Mohr des transformations
Dans le plan (ε, r) c'est l'équation d'un cercle que l'on pourrait appeler le Cercle de Mohr des transformations car il fait intervenir les déformations et la rotation
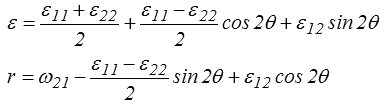
Ce cercle est centré en (( ε11+ε12 ) / 2 , ω21 = ( ε21−ε12 ) / 2), et lorsque le vecteur matériel tourne d'un angle θ dans le plan physique, le point correspondant tourne dans le plan de Mohr d'un angle double et en sens contraire( point générique en rouge ci-dessous).
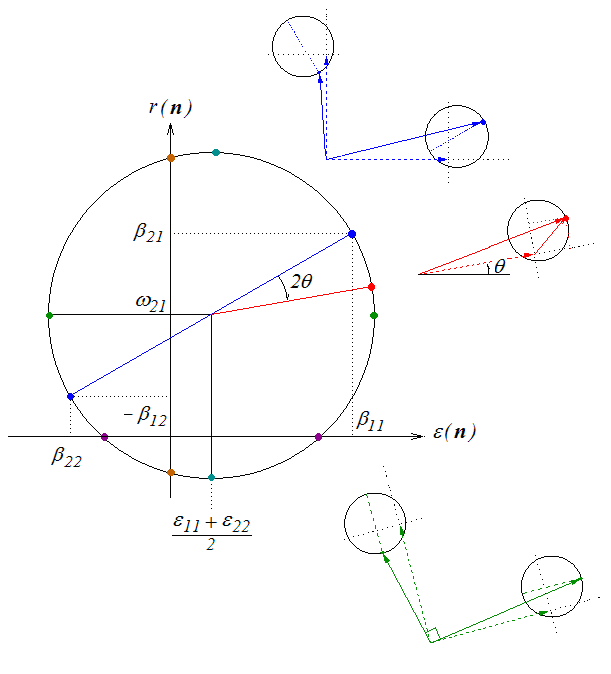
Construction et utilisation
Comme pour le tenseur des contraintes on peut construire ce cercle à partir des deux directions x1 et x2.
- Direction x1 ε = β11 , r = β21
- Direction x2 ε = β22 , r = −β12
Comme pour les contraintes, on obtient : - Les directions principales (points verts) qui tournent toutes deux de la rotation ω21 (et restent donc perpendiculaires, pas de glissement ; pourtant sur le dessin elles ne semblent pas perpendiculaires ! ?)parce que, comme toujours lorsqu'on représente en HPP les déformations, il faut les amplifier pour les rendre visibles. Ceci peut induire des perturbations troublantes.
- Les directions qui minimisent et maximisent la rotation, et qui correspondent donc à la valeur maximale du glissement (points turquoise).
On peut de plus obtenir, lorsqu'elles existent, - Les directions d'allongement nul (points orange),
- Les directions invariantes (rotation nulle, points grenat).
Animation
Cette animation permet de visualiser, dans le plan physique et dans le plan de Mohr, l'évolution du vecteur du selon l'orientation du vecteur dx. Vous pouvez la télécharger et vous trouverez ici comment l'utiliser
Je vous conseille là encore de tester diverses transformations et, pour bien comprendre ce qui se passe, de figer l'animation en basculant d'un mode d'affichage à l'autre.