Mécanique du point matériel
La mécanique du point matériel est évidemment un chapitre important, le premier chapitre de tout cours de physique en fait. Il est toutefois très largement traité par ailleurs, et je me limiterai à une présentation de ce dont j'aurai besoin dans la suite.
Les lois de Newton
L'essentiel est traditionnellement regroupé dans les trois lois de Newton. L'excellent article de Wikipedia (w) en donne une présentation couvrant à la fois leur contenu et le contexte historique.
Première loi : Principe d'inertie.
Un corps libre de toute action extérieure suit un mouvement rectiligne uniforme.
Il faut bien réaliser le caractère profondément révolutionnaire de cette affirmation, absolument contraire à notre expérience quotidienne. C'est, pour beaucoup d'entre nous, le vrai début de la physique.
Seconde loi.
m γ = f
f force exercée,
m masse,
γ = d V / d t = d 2OM / d t 2 accélération.
C'est le prolongement naturel du principe d'inertie : puisqu'une action extérieure ne change pas la vitesse, dérivée première de la position, elle n'agira sans doute que sur la dérivée suivante, l'accélération. Il fallait toutefois, pour ce prolongement, inventer le calcul différentiel !!
Troisième loi : Principe d'action-réaction.
La force exercée par un corps A sur un corps B est opposée à la force exercée par B sur A.
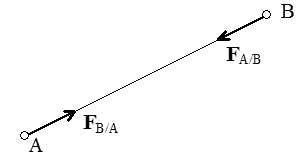Par opposé il faut entendre que ces deux vecteurs sont à la fois égaux au signe près et alignés.
FA/B = − FB/A AB ∧ FB/A = 0
L'énoncé de ces lois pose évidemment nombre de questions (qu'est-ce qu'un corps ? une force ? la masse ?...). Le corps, ici, est un point matériel, c'est-à-dire un objet suffisamment petit pour pouvoir être assimilé à un point géométrique, donc de taille nulle. On verra plus loin que le théorème du centre d'inertie sécurise cette assimilation (>).
Changement de référentiel
Parmi toutes ces questions, je n'évoquerai que la question du référentiel d'observation. La vitesse et l'accélération dépendent en effet du référentiel, c'est-à-dire du système d'axes utilisé par l'observateur pour décrire le mouvement.
Soit par exemple deux référentiels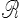 
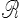o et 1 en mouvement l'un par rapport à l'autre
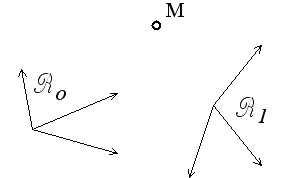
On démontre classiquement les formules de composition des vitesses et des accélérations (w)
vo = v1 + ve
γo = γ1 + γe + γc
où vo [resp. γo] est la vitesse [resp. accélération] « absolue » du point M, c'est-à-dire mesurée par un observateur lié à 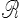o.
De même v1 et γ1 représentent la vitesse et l'accélération « relatives », c'est-à-dire mesurées par un observateur lié à 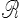1 , elles sont traditionnellement notées vr et γr,
tandis que ve et γe représentent la vitesse et l'accélération d'« entraînement », c'est-à-dire celles du point matériel M1 attaché à 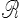1 mais qui, à l'instant considéré, coïncide avec M, et mesurées par rapport à 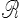o,
enfin, le terme γc
γc = 2 Ω (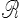1 /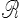o ) ∧ vr ( vr = v1 )
représente l'accélération dite de Coriolis.
Référentiel galiléen
Puisque l'accélération dépend du référentiel utilisé pour suivre le mouvement, c'est-à-dire en fait de l'observateur, la seconde loi de Newton n'aura de sens que si l'on précise ce référentiel − ou alors il faudrait admettre que la force en dépend également, ce que nous refusons pour l'instant d'envisager. Nous devons donc supposer qu'il existe un référentiel en quelque sorte absolu et corriger la loi
Seconde loi.
Dans le référentiel absolu
m γ = f
f force exercée,
m masse,
γ = d V / d t = d 2OM / d t 2 accélération.
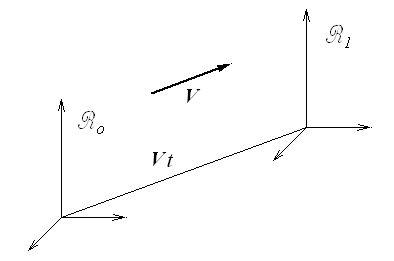Mais tout référentiel en translation uniforme par rapport au référentiel absolu conduira à la même accélération et la seconde loi de Newton y restera donc valable. On nomme référentiel galiléen tout référentiel en translation uniforme par rapport au référentiel absolu. Nous devons encore corriger notre loi :
Seconde loi, version finale.
Dans tout référentiel galiléen
m γ = f
f force exercée,
m masse,
γ = d V / d t = d 2OM / d t 2 accélération.
On dit également que la mécanique newtonienne satisfait l'invariance galiléenne, ce qui, entre autres conséquences, implique que, sitôt postulée l'existence d'un référentiel absolu, il faut immédiatement accepter le fait que la mécanique ne permettra pas de le mettre en évidence. C'est là, dit-on, la cause réelle des ennuis de Galilée avec l'Inquisition.
Forces d'inertie
Et si, pour une raison ou une autre, on souhaite travailler en référentiel non galiléen, alors il faudra prendre en compte, dans l'accélération, les termes correctifs (accélération d'entraînement et accélération de Coriolis) dûs au mouvement du référentiel d'observation. Il est souvent commode de les transférer au second membre.
Seconde loi en référentiel non galiléen :
m γ = f + f inertie f inertie = − m γe − m γc
introduisant une force fictive, dite d'inertie, prenant en compte cette correction.
Référentiel terrestre
On considère usuellement qu'un référentiel galiléen acceptable est un repère centré au Soleil et dont les directions sont fixées par rapport aux étoiles. Quelles sont les conséquences sur Terre ? puisque c'est bien là que se poseront la plupart des problèmes qui nous intéressent ici.
Nous devons donc prendre en compte les termes correctifs liés au mouvement de notre référentiel d'observation, usuellement le « référentiel du laboratoire », lié à l'espace tel que nous le percevons. Ce mouvement inclut
- la translation non uniforme de la Terre dans son mouvement autour du Soleil. Je ne connais pas de situation réclamant la prise en compte de cette correction ;
- la rotation de la Terre, qui va introduire deux termes correctifs ou forces d'inertie :
- la force d'inertie d'entraînement sera ajoutée à la force d'attraction universelle, participant ainsi à la gravité locale,
- la force d'inertie de Coriolis, liée à la vitesse, sera en général négligée sauf pour quelques problèmes spécifiques, par exemple le sens de rotation des alizés en mécanique de l'atmosphère.