Le modèle élastique
Le comportement élastique
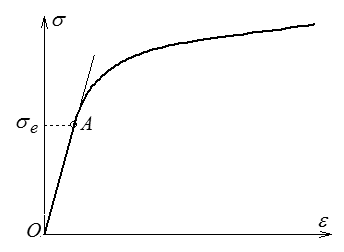On a représenté ci-contre la courbe de traction d'un matériau métallique. La partie OA de cette courbe correspond à un comportement linéaire (la contrainte est proportionnelle à la déformation) et réversible (le retour en arrière se fera sur la même courbe OA).
Au-delà du point A on entre dans le domaine plastique, qui correspond à un comportement non linéaire et irréversible.
Le modèle élastique linéaire correspond à cette première phase de la réponse du matériau. Dans le cas monodimensionnel ce modèle est donc constitué par deux ingrédients :
- Une relation linéaire entre contrainte et déformation
σ = E ε E : module d'Young
C'est la loi élastique à proprement parler. - Une condition de validité
σ ≤ σe σe : limite d'élasticité
que nous appellerons critère de limite d'élasticité.
Bien évidemment, et comme toujours sitôt qu'intervient l'expérience, cette description correspond déjà à une certaine idéalisation de la réalité. La courbe expérimentale, ou plutôt en général l'ensemble des points expérimentaux, présentera toujours quelques écarts par rapport à cette idéalisation. Ces écarts proviennent à la fois des imprécisions expérimentales et de l'approximation du modèle théorique. La détermination de la constante de proportionnalité E ne pose en général pas de problème insurmontable (régression linéaire, ou en termes plus savants méthode des moindres carrés), il n'en va pas de même pour la limite élastique σe, qui, même à partir de résultats expérimentaux très précis, ne peut être déterminée sans un certain arbitraire. Cette valeur est largement conventionnelle. Dans les applications industrielles elle sera d'ailleurs souvent fixée par la réglementation.
Nous sommes partis ici du comportement des matériaux métalliques. Ce cas est certainement important, mais on aurait en fait obtenu des résultats similaires avec d'autres matériaux (béton, composite, bois, os,...). Ce modèle élastique linéaire est incontestablement le modèle le plus utilisé en mécanique des solides (exclusivement ou en première approximation).
Le modèle élastique
Le modèle élastique est réversible, donc sans dissipation. Dans le cadre de la Mécanique des Milieux Continus en petites perturbations ceci se traduit simplement par (<)
σij 
ij = 
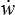ø = 0
Il est donc alors naturel de supposer que l'énergie w est simplement fonction de la déformation w = w(εij ), on en déduit alors simplement
.
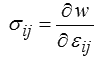La contrainte s'obtient par dérivation de la fonction énergie w par rapport à la déformation.
L'énergie doit être positive: il faut fournir de l'énergie pour déformer le matériau (si tel n'était pas le cas, il se déformerait spontanément - on évoque ici traditionnellement la stabilité du matériau). En général, on suppose de plus que cette énergie w est fonction convexe de la déformation.
C'est cette relation que nous prendrons comme définition d'un matériau élastique . Cette loi de comportement donne les contraintes en fonction des déformations. Il est souvent nécessaire d'inverser cette relation pour calculer les déformations en fonction des contraintes. Pour ce faire, on introduit la quantité
w c = σij εij − w(εij ) = w c(σij )
exprimée en fonction des contraintes.
On obtient alors par différentiation
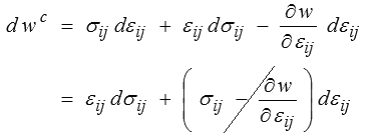
qui permet donc d'écrire
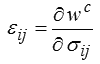
Cette fonction w c(σ) est souvent appelée « énergie complémentaire », mais le lecteur ne doit pas se laisser abuser par cette terminologie, cette quantité n'a aucune signification énergétique directe, il s'agit en fait d'une transformation mathématique (transformation de Legendre; c'est notamment ici que la convexité de la fonction w arrange bien les choses!) ; nous n'insistons pas davantage pour l'instant.
Critères de limite d'élasticité
Comme tout modèle de comportement, l'élasticité est une idéalisation. Très courante dans les applications, elle ne sera toutefois raisonnable que pour des sollicitations limitées. Après avoir trouvé la solution d'un problème il faudra vérifier a posteriori que cette solution reste bien dans ces limites.
Ce qui se passe si l'on atteint cette limite dépend du matériau :
- rupture ou endommagement (comportement fragile)
- déformations irréversibles, plasticité (comportement ductile)
mais cela ne nous concerne pas ici − le calcul élastique interdit justement d'y arriver. On parlera de dimensionnement élastique puisque c'est cette condition de limite d'élasticité qui dans la conception d'une structure imposera des dimensions minimales pour pouvoir résister aux sollicitations imposées. Insistons à nouveau toutefois sur le caractére conventionnel, et même souvent réglementaire de cette limite: la rupture, si rupture il y a, implique toujours des aspects statistiques tandis que les déformations irréversibles n'apparaissent que progressivement et ne seront donc considérées comme telles qu'à partir d'un certain niveau lui aussi conventionnel.
Traditionnellement on exprime cette condition en fonction des contraintes, mais en élasticité on pourrait tout aussi bien choisir de l'exprimer en fonction des déformations, puisque la loi de comportement donne justement les contraintes en fonction des déformations.
Très souvent cette condition de limite d'élasticité pourra s'écrire sous forme d'une inégalité
f(σij ) ≤ 0
introduisant la fonction seuil f. Ceci suppose en fait que le domaine d'élasticité est suffisamment régulier. Ce n'est pas toujours le cas, mais nous nous limiterons le plus souvent à cette écriture.