Le tenseur des déformations
Le tenseur des déformations (infinitésimales) εij est dual du tenseur des contraintes, et on peut largement transposer tout ce qui avait alors été dit (<).
Les composantes du tenseur des déformations
La signification des composantes εij découle directement de la description des déformations telle qu'elle a été présentée plus haut. En effet, l'allongement dans la direction x1, et le glissement dans des directions (x1 , x2 ) sont directement donnés par
ε11 = ε (e1 ) 2 ε12 = γ (e1 , e2 )
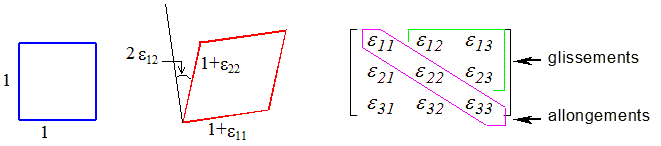
Partant d'un cube d'arête unité, les composantes diagonales représentent l'allongement des arêtes tandis que les composantes hors diagonale représentent leur glissement, c'est-à-dire leur variation d'angle.
Changement de repère
Les formules de changement de repère s'obtiennent comme pour le tenseur des contraintes (<). On peut par exemple partir de la définition de l'allongement, quantité scalaire indépendante du repère
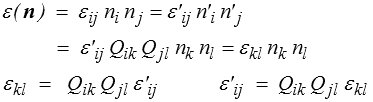
et on retrouve la même règle de transformation que pour le tenseur des contraintes.
D'un point de vue mathématique, on peut toutefois remarquer que le tenseur des contraintes est essentiellement une application linéaire qui au vecteur n associe le vecteur T, tandis que le tenseur des déformations est plutôt une forme quadratique qui à un vecteur n associe l'allongement ε(n), ou une forme bilinéaire qui à deux vecteurs m, n associe leur glissement γ(m,n). Or si l'on se réfère aux livres de mathématiques, on trouvera les applications linéaires et les formes quadratiques traitées dans des chapitres différents et avec des règles de changement de repère différentes...? La solution de ce paradoxe apparent tient au fait que nous travaillons en repère orthonormé, et on vérifie facilement que, dans ce cas, c'est-à-dire avec une matrice de passage orthogonale, ces formules coïncident. Plus fondamentalement, ceci résulte de la structure euclidienne de l'espace de la physique newtonienne, qui permet de l'identifier à son dual. Il convient par contre de tirer profit de cette structure en travaillant en repère orthonormé, sinon il faudra distinguer composantes covariantes et contravariantes, et les choses deviennent − techniquement, la physique reste bien sûr la même − beaucoup plus compliquées (vraiment beaucoup !, et je déconseille formellement au lecteur, même aventureux, de travailler en repère non orthormé s'il n'y est pas vraiment obligé).
Allongements principaux
En repère principal les termes hors diagonale sont nuls, les angles droits sont donc conservés et la déformation transforme un cube en parallélépipède rectangle (ce parallélépipède peut de plus tourner, mais cela ne concerne pas la déformation)
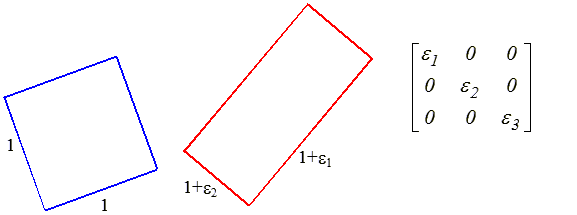
Comme pour les contraintes, ces allongements principaux (ou déformations principales, mais ce sont effectivement des allongements) se calculent par résolution de l'équation caractéristique
Pε (λ) = det (ε − λ1) = −λ3 + εI λ2 − εII λ + εIII = 0
en introduisant les invariants principaux de ε (<).
Déviateur et partie sphérique
Contrairement au cas des contraintes (<), cette décomposition

a, pour le tenseur des déformations, une signification physique claire. On vérifie en effet facilement que εI caractérise la variation de volume
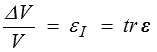
Il suffit, pour s'en convaincre, de partir d'un cube unité (V = 1) dans les axes principaux, et de calculer le volume du parallélépipède rectangle déformé
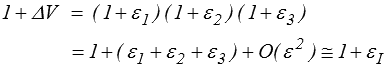
Ainsi la partie sphérique représente une dilatation (si elle est positive, une contraction sinon) uniforme dans toutes les directions, tandis que le déviateur correspond à une déformation isochore (sans variation de volume), nous parlerons désormais de distorsion (attention toutefois, cette terminologie est assez courante mais non universelle ; on pourra retrouver ce terme « distorsion » avec des significations trés variées).
