Description des déformations
En introduisant le théorème des travaux virtuels ou puissances virtuelles nous avons insisté sur le fait qu'il fallait plutôt le voir comme définissant le travail ou la puissance des efforts intérieurs. C'est bien ce que nous avons fait ici et c'est ainsi que dans le cadre de la MMC HPP (<) nous avons introduit le tenseur des déformations εij (déformations infinitésimales stricto sensu, mais nous nous limitons désormais au cadre HPP et nous omettrons ce qualificatif. Il faudra par contre y revenir en abordant les grandes déformations).
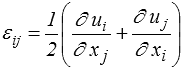
Variation du produit scalaire
Un solide rigide, c'est-à-dire non déformable, est caractérisé par le fait que les longueurs et les angles n'y changent pas. Les déformations sont donc intuitivement associées aux variations de longueurs et d'angles.
D'un point de vue technique ces variations de longueurs et d'angles pourront être calculées à partir des variations de produit scalaire.
Considérons donc deux vecteurs matériels d x et δ x. Après déformation ces vecteurs deviennent respectivement d x' et δ x'.
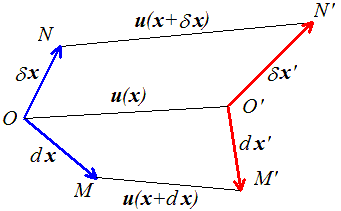
Remarquons au passage que nous aurions dû plutôt partir de deux vecteurs d X et δ X devenant d x et δ x. Toutefois l'hypothèse des petites déformations avait comme première conséquence l'identification de X à x, et nous avons choisi de conserver la notation x. Il faudra bien évidemment revenir aux notations originales pour aborder les grandes déformations. Rappelons également que dans le dessin ci-dessus les déformations sont, comme toujours en HPP, amplifiées : elles sont en réalité petites et seraient, représentées en vraie grandeur, indiscernables. Après déformation le vecteur d x devient
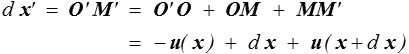
soit, en composantes et au premier ordre, (bon exercice de manipulation des notations indicielles !)
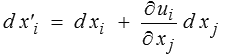
Le produit scalaire des deux vecteurs sera donc
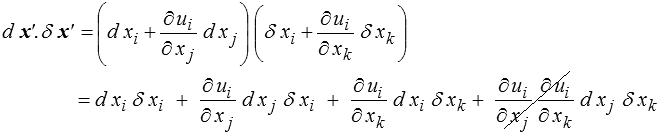
Le dernier terme est du second ordre par rapport aux ∂ ui / ∂xj et on aura donc au premier ordre
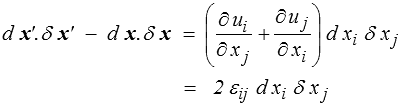
relation fondamentale qui fait intervenir le tenseur εij qui apparaissait déjà dans le théorème des travaux virtuels et qui nous conforte donc dans son interprétation comme description des déformations.
Allongement dans une direction
En prenant dans la formule précédente d x = δ x, il vient
d x' 2 − d x 2 = 2 εij d xi d xj
en notant dx' = |d x'| , dx = |d x| et n = d x / dx (vecteur unitaire dans la direction d x)
dx' 2 = dx 2 + 2 εij d xi d xj = dx 2 (1 + 2εij ni nj )
soit, en prenant la racine de cette expression et au premier ordre,
dx' = dx (1 + εij ni nj )
On définit l'allongement dans la direction n comme étant la variation relative de longueur d'un vecteur matériel orienté dans cette direction
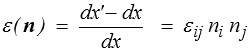
Les quantités εij permettent donc de calculer les allongements dans toutes les directions.
Glissement dans deux directions perpendiculaires
Nous prenons maintenant d x et δ x perpendiculaires
d x = dx n δ x = δx m
On obtient alors
d x' . δx' = d x . δ x + 2 εij d xi δ xj
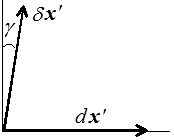On appelle glissement γ la variation d'angle
γ = π/2 − (d x', δ x')
et il vient directement
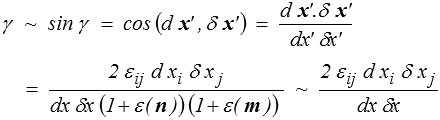
soit, au premier ordre,
γ(m, n) = 2 εij ni mj
Les quantités εij permettent donc également de calculer les variations d'angles (nous nous sommes ici limités au glissement, c'est-à-dire au cas de deux directions perpendiculaires, mais on pourrait mener un calcul plus lourd, mais analogue, pour deux directions quelconques).
Description du mouvement local
Un autre éclairage sur la signification des εij comme caractérisation des déformations découle de la description du mouvement autour d'un point xo. On peut en effet écrire au premier ordre
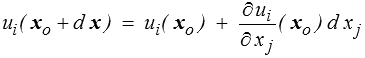
On décompose ensuite le gradient du déplacement en partie symétrique et antisymétrique
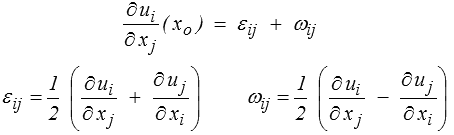
qui permet d'écrire
ui (xo + d x) = uio + ωijo d xj + εijo d xj
en notant uio, εijo et ωijo la valeur en xo des quantités correspondantes.
Le premier terme constant est une translation, le second terme est une rotation, comme l'on peut aisément s'en convaincre en introduisant le vecteur ω adjoint du tenseur antisymétrique ωij (<)
ωij = ∈ijk ωk ωij d xj = − (ω∧d x)i
On peut donc écrire
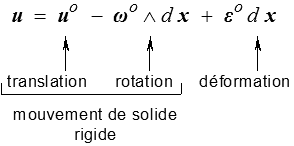
Le mouvement local du milieu continu est la superposition d'un mouvement de solide rigide et de la déformation.
Une remarque importante
Dans beaucoup d'exposés classiques de mécanique des milieux continus (y compris dans mon cours polycopié) on part des considérations développées ici pour introduire les déformations, après avoir défini comme plus haut les contraintes (ou avant de l'avoir fait, peu importe en fait car les deux raisonnements semblent alors complètement indépendants), pour constater ensuite, oh ! miracle, que les deux notions sont en fait couplées (on dit « duales ») par le travail des efforts intérieurs. Une telle approche occulte complètement cette nécessaire dualité, et le lecteur est invité à bien s'imprégner du fait que, en mécanique, les descriptions des efforts et des déformations sont indissociablement liées et que, une fois choisie l'une, l'autre s'impose. Ici nous sommes partis des efforts et nous en avons déduit les déformations. Dans d'autres cas, on pourra trouver plus commode de partir des déformations et d'en déduire les contraintes, mais, sauf à être très chanceux ou particulièrement bien inspiré, on ne peut postuler les deux indépendamment.